
文章目录
视频链接
根据视频整理
智能优化算法系列2 BP神经网络基本原理简介
1 引例
以我们认识一个人为例。
我们在日常生活中,认识一个人并且能在之后的一段时间内认出并正确说出其对应的名字,主要是通过该人的五官特征与其名字之间的对应关系实现的。
在最开始,一个人自我介绍,“我叫某某某,来自…”,对于我们来说,认识这个人并在未来的一段时间内能够认出并说出与其对应的姓名,其实就是建立一个该人的五官特征或者其他外貌特征(这里仅以面部特征为例)与其姓名的对应关系。
而该项工作,主要是由我们大脑中的神经元组成的神经网络实现的。对于我们大脑中的神经网络来说,建立该对应关系,需要一定的输入(即该人的面部特征),以及在该输入下与之对应的输出(即姓名),外加不同面部部位对最终结果的影响程度(即权重)。
在此,我们选取面部中的眼睛、鼻子、嘴巴为输入变量,对应的输出结果为老王,其中眼睛、鼻子、嘴巴对应的符号为a 1 , a 2 , a 3 a_{1}, a_{2}, a_{3}a1,a2,a3,对应的权重(即对最终结果的影响程度)为w 1 , w 2 , w 3 w_{1},w_{2},w_{3}w1,w2,w3,结果为y = 老王 y = \text{老王}y=老王。
据此,我们可以建立一个函数关系式:
y = w 1 a 1 + w 2 a 2 + w 3 a 3 y = w_{1} a_{1} + w_{2} a_{2} + w_{3} a_{3}y=w1a1+w2a2+w3a3
认识老王后,即建立了如上的关系表达式。之后,我们再次遇见老王,只要向我们大脑的神经网络中输入老王对应的眼睛、鼻子、嘴巴的特征值,然后通过向前建立的对应关系(函数关系式),我们即可判断其的姓名为老王。
当然,如果某天老王因为意外而导致眼睛、鼻子受伤,导致其眼睛、鼻子的特征值发生改变,可能导致我们再次遇见老王时,对其判断出错,与真实姓名不符,即存在误差。
但是如果老王受伤较轻,只是鼻子特征改变,而鼻子在关系式中对结果的影响程度特别小,我们依旧可以根据其他两个特征(对结果的影响程度大,即权重大)正确判断出该人为老王。由此,建立关系式时,正确合适的权重很重要。
人工神经网络,就是模仿人大脑的神经网络来进行构建与实现的
由引例,我们可得:
神经网络的四大基本组成部分为:
(1)特征输入
(2)标准输出
(3)权重
(4)误差
2 人工神经网络的概述
2.1 概述
人工神经网络是人脑及其活动的一个理论化的数学模型,由大量的处理单元通过适当方式互连构成,是一个大规模非线性自适应系统。人工神经网络具有并行分布处理、高度容错、自组织、自适应以及自学习功能,能分析较为复杂的非线性系统。此外,人工神经网络方法能从已知数据中自动归纳规则,获得这些数据的内在规律,具有很强的非线性映射能力。由于神经网络不需要对知识进行深入挖掘提炼,只需用适当的数据对神经网络进行训练即可将知识固定在网络的节点上,因而可以减少知识获取的时间。同时,神经网络的特性决定了当其遇到某个无法确立征兆和原因对应关系的故障时,依然能够对数据进行学习并以网络结构的形式将知识固化。
[1]吕金飞.基于人工神经网络的发射塔平台设备故障诊断[J].信息与电脑(理论版),2022,34(01):4-7.
人工神经算法主要通过模拟人的大脑组织进行运算,其主要由以下三部分构成:“树突”、“轴突”和“细胞体”,三者之间相互连接,同时也各自具有特定的功能。信息由“树突”输入,经“细胞体”处理后,再由“轴突”输出,传递到下一个“神经元”当中。当然,如输出到下一个“神经元”的信号参数尚未达到临界值,则下一个“神经元”则处于抑制状态,不会传递相应的信号。相对于人的大脑的细胞神经元而言,人工神经网络算法在此基础上进行了一定的简化,神经元的输入和输出的关系可表示为:
I i = ∑ j = 1 n w i j x j − θ i I_{i}=\sum_{j=1}^{n} w_{i j} x_{j}-\theta_{i}Ii=j=1∑nwijxj−θi
y i = f ( I i ) y_{i}=f\left(I_{i}\right)yi=f(Ii)
在公式中,x j x_{j}xj(j jj为正整数)是从各个神经元组织传递进来的信息,w i j w_{ij}wij则表示神经元i ii和神经元j jj之间传递的权值。
[1]史腾飞,吴娟.人工神经网络在水文领域中的应用[J].电子测试,2022,36(02):38-40.DOI:10.16520/j.cnki.1000-8519.2022.02.021.
$$I_{i}=\sum_{j=1}^{n} w_{i j} x_{j}-\theta_{i}$$
$$y_{i}=f\left(I_{i}\right)$$
$x_{j}$
$j$
$w_{ij}$
$i$
$j$
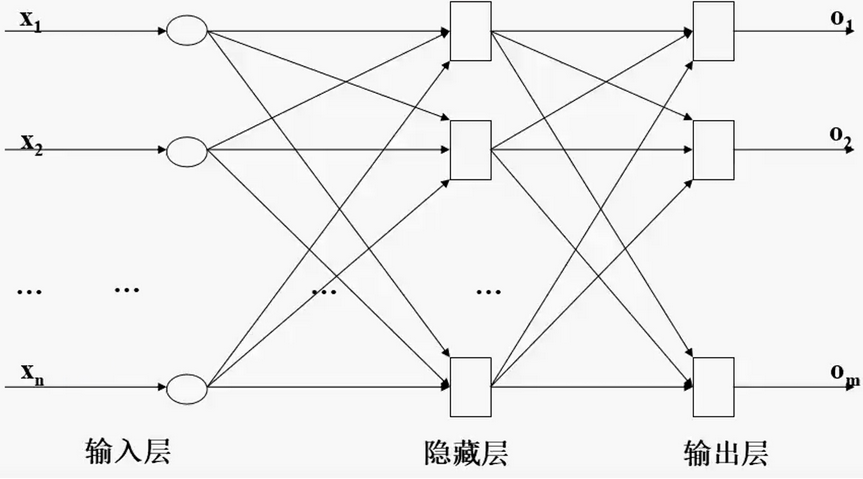
2.2 神经网络的典型结构图
层与层之间的神经元是全连接关系;在同一层中,各列之间的神经元保持相互独立。
这里层为竖向,列为横向
3 人工神经网络的适用场景
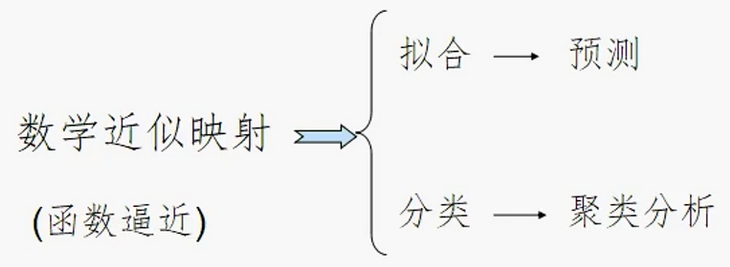
人工神经网络可以用于:
(1)分类问题
(2)评价问题
(3)预测问题
4 人工神经网络模型的分类
根据神经网络中神经元的互联方式的不同,人工神经网络模型可以分为:
(1)前馈神经网络模型
(2)反馈神经网络模型
(3)自组织网络模型
4.1 前馈神经网络模型
只在训练过程会有反馈信号,而在分类过程中数据只能向前传送,直到到达输出层,层间没有向后的反馈信号。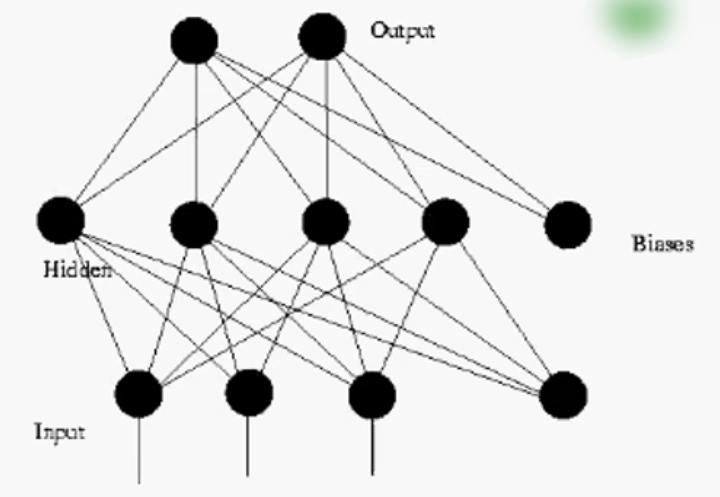
4.2 反馈神经网络模型
从输出到输入具有反馈连接的神经网络,其结构比前馈网络要复杂得多。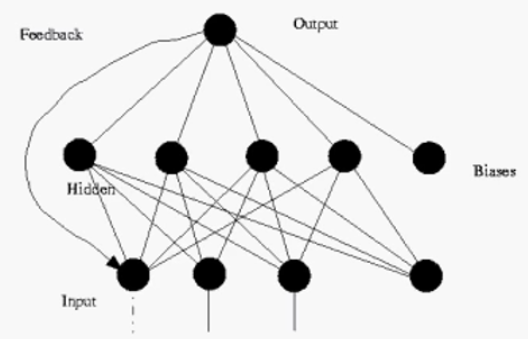
4.3 自组织网络模型
通过自动寻找样本中的内在规律和本质属性,自组织、自适应地改变网络参数与结构。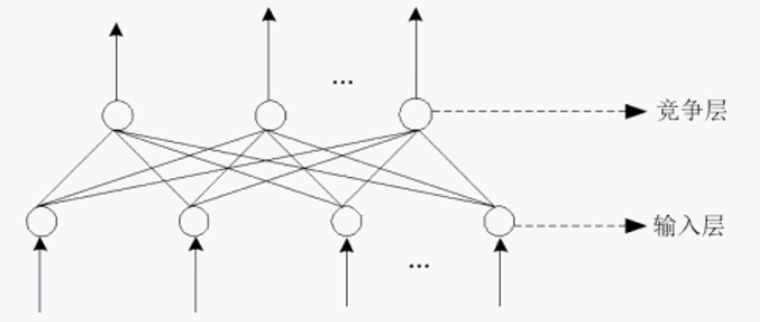
5 建立和应用神经网络的步骤
5.1 网络结构的确定
包含网络的拓扑结构和每个神经元相应函数的选取;
5.2 权值和阈值的确定
通过学习得到,为有指导的学习,也就是利用已知的一组正确的输入、输出数据,调整权和阈值使得网络输出与理想输出偏差尽量小;
神经网络最主要的是权值的构建,神经网络要产生一个反馈的过程需要设置一个阈值,且达到该阈值才会有反馈的过程。
5.3 工作阶段
用带有确定权重和阈值的神经网络解决实际问题的过程,也叫模拟(simulate) 。
5.4 工作状态
工作状态包括学习和工作两种状态
5.4.1 学习状态(权重的确定)
利用学习算法来调整神经元间的连接权重,使得网络输出更符合实际。
学习的方式分为:
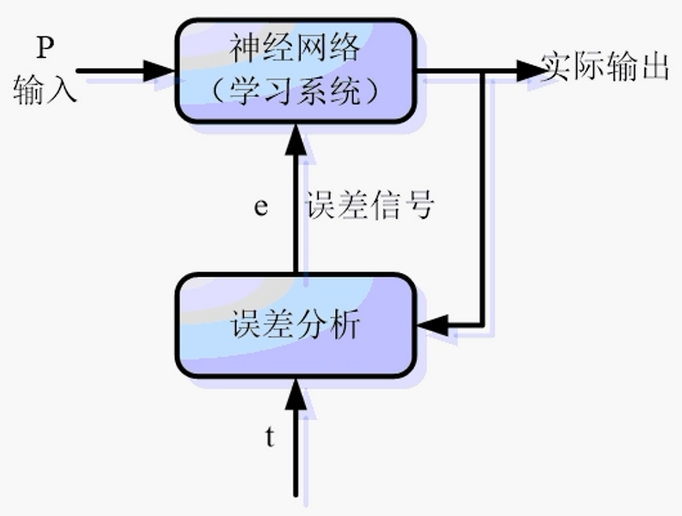
(1)有导师学习(监督学习)
将一组训练集送入网络,根据网络的实际输出与期望输出间的差别来调整连接权值。
例如:BP算法
有导师学习需要一个标准输入与一个标准输出
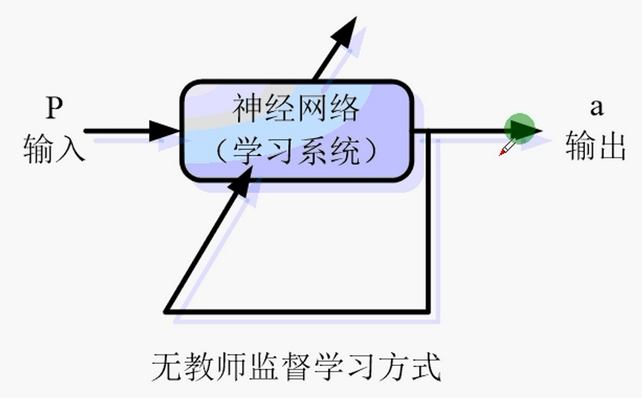
(2)无导师学习
抽取样本集合中蕴含的统计特性,并以神经元之间的联接权的形式存于网络中。
例如:Hebb学习率
无导师学习由于没有一个确切的标准,所以在一个网络内,不同的神经元所采取的方式会有些许不同,所以可能会导致最后的结果出现混乱等。
一般使用有导师学习
5.4.2 工作状态(工作阶段解决问题)
神经元间的连接权值不变,可以作为分类器或者预测数据之用。
6 激活函数

6.1 激活函数的类别
线性函数一般用于隐含层到输出层之间的激活函数
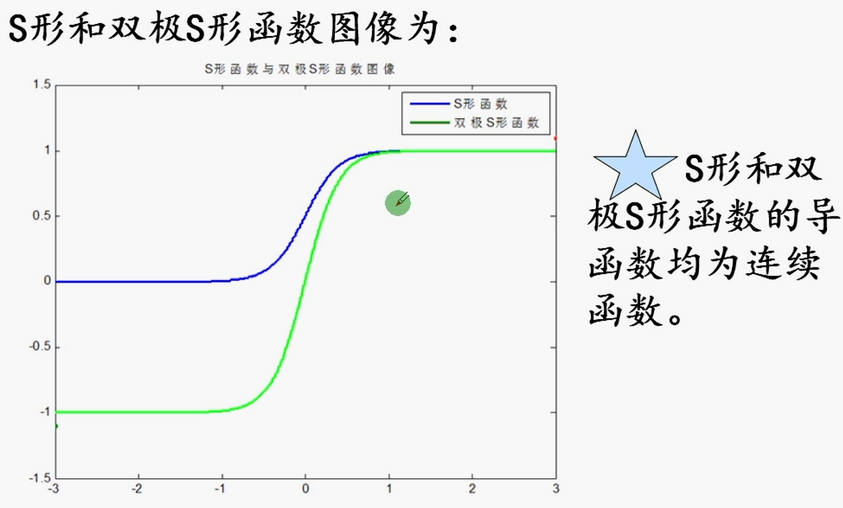
其他的激活函数一般使用S形函数或双极S形函数,其中,更多的使用双极S形函数。
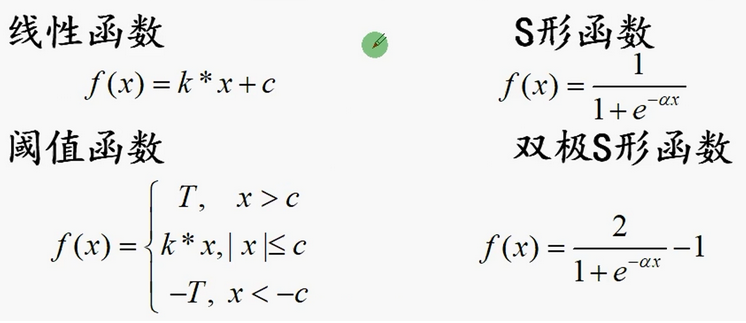
7 BP神经网络模型的建立
7.1 人工神经网络的概述(理论介绍)
多层感知器( multi-layer perceptron,MLP) 也叫人工神经网络( artificial neural network,ANN) ,是一种运算模型,旨在模拟神经系统构造与功能进行数据处理,从信息处理角度对人脑神经元网络进行抽象模拟,由大量的节点(或称神经元) 相互联接构成,通过不断调整模拟神经元之间链条的权值,使得整个网络可以较好地拟合训练数据的关系。
[1]孙凤娟,田勇,孙开争,付华轩,张文娟,李敏,吕晨.基于人工神经网络集合预报的济南市臭氧预报方法[J].山东科学,2022,35(03):89-99.
人工神经网络的基本组成是人工神经元,人工神经元从结构和功能的角度模拟和抽象生物神经元,人工神经元是通过模拟人脑中神经元的结构和相互联系而建立的数学模型。
[1]陈成龙. 基于人工神经网络的油田开发数据分析及预测研究[D].东北石油大学,2022.DOI:10.26995/d.cnki.gdqsc.2022.000046.
通过对人脑神经元的分析与简化,得到简易的人工神经元数学模型,如图所示: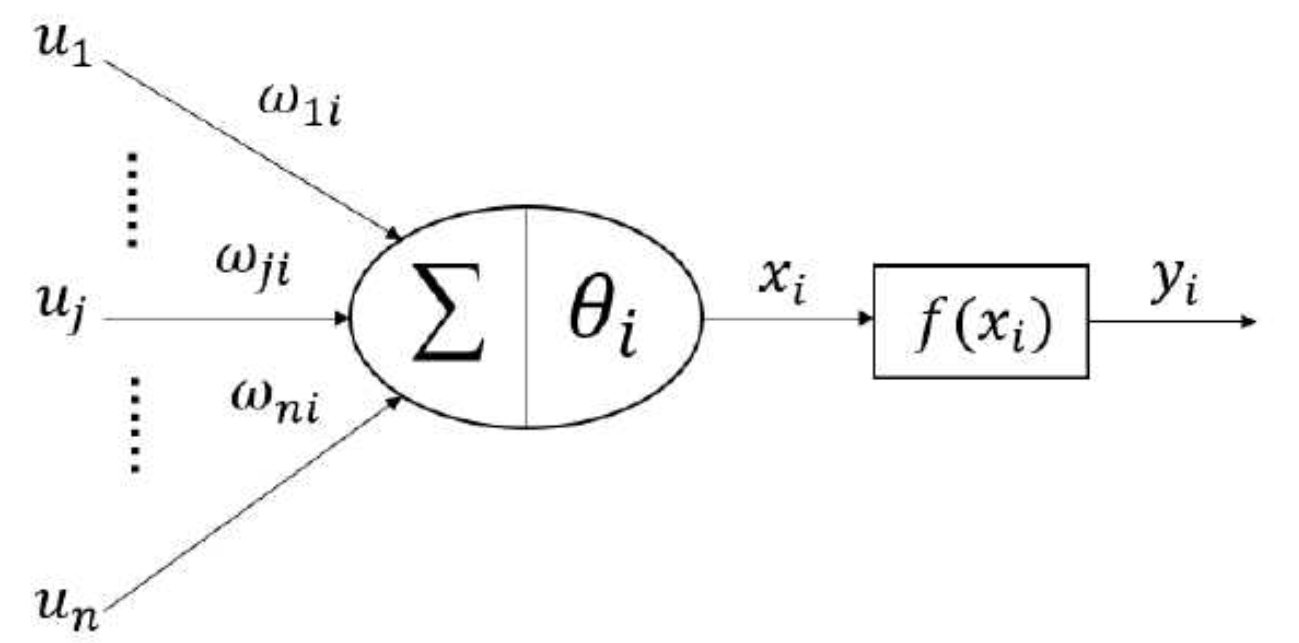
其中,u 1 , u 2 , . . . , u n u_{1}, u_{2}, ..., u_{n}u1,u2,...,un为对人工神经元i ii的多个输入信号,y i y_{i}yi为人工神经元i ii对应的输出值,w j i w_{ji}wji为第i ii个人工神经元的第j jj个输入信号的连接权值,θ i \theta_{i}θi为第i ii个人工神经元的阈值,x i x_{i}xi为第i ii个人工神经元对所有的输入信号根据权值求和后的净输入,f ( x i ) f(x_{i})f(xi)为第i个人工神经元的激励函数。
第i ii个人工神经元的净输入为:
x i = ∑ j = 1 n ω j i u j − θ i x_{i}=\sum_{j=1}^{n} \omega_{j i} u_{j}-\theta_{i}xi=j=1∑nωjiuj−θi
第i ii个人工神经元的激励函数表达式为:
y i = f ( x i ) = f ( ∑ j = 1 n ω j i u j − θ i ) y_{i}=f\left(x_{i}\right)=f\left(\sum_{j=1}^{n} \omega_{j i} u_{j}-\theta_{i}\right)yi=f(xi)=f(j=1∑nωjiuj−θi)
人工神经网络由多个人工神经元组成,其结构主要分为输入层、隐含层和输出层,人工神经网络模型结构如图所示: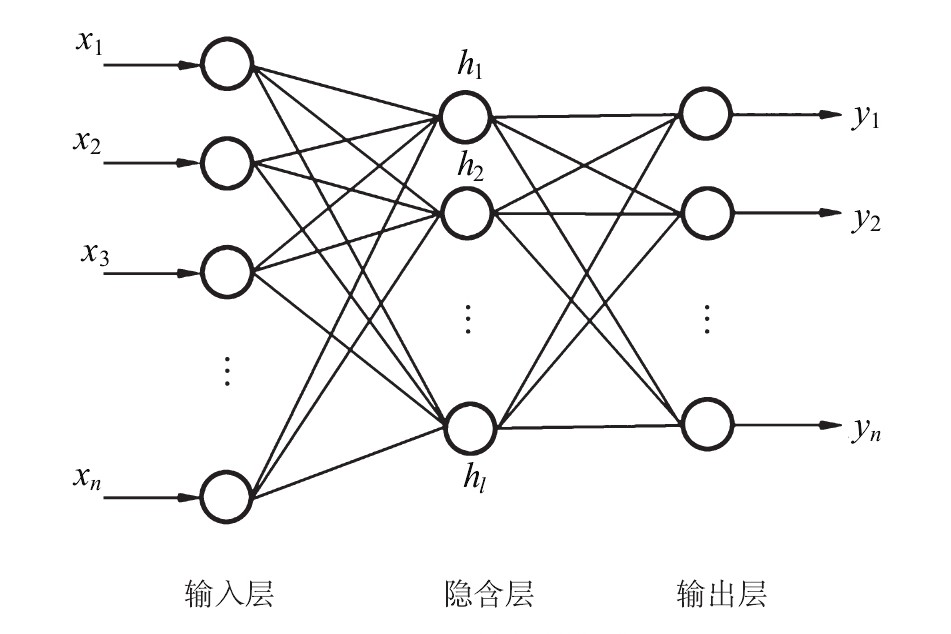
7.2 BP算法基本原理
BP算法(Back Propagation,BP)就是利用输出后的误差来估计输出层的直接前导层的误差,再用这个误差估计更前一层的误差,如此一层一层的反传下去,就获得了所有其他各层的误差估计。
[1] 宋文娟,席永胜,佟明勇.基于BP算法的工程造价散材量估算方法[J].甘肃科技,2020,36(14):91-93.
7.3 BP神经网络的概述
BP的英文全称是Back Propagation,也被称作 Error Back Propagation,翻译为误差反向传播,误差反传是BP神经网络算法的最大优点。BP神经网络具有自适应和自学习等特点。BP神经网络分为信号正向传播与误差反向传播。正向传播过程中,预测模型的样本数据信息从输入层传入,后经过隐藏层的处理,最终传向输出层。若网络预测输出值与网络期望输出值相差较大时,误差将会反向逐层分摊给各层,直到误差达到要求的精度范围内停止循环。
[1]陈成龙. 基于人工神经网络的油田开发数据分析及预测研究[D].东北石油大学,2022.DOI:10.26995/d.cnki.gdqsc.2022.000046.
信号的正向传播,误差的反向传播。
隐含层节点数是一个非常重要的参数,它的设置对BP神经网络性能的影响很大,隐藏层节点数目的确定,仍是BP神经网络目前最难解决的问题之一,目前还没有很好的解决方法,只能通过试验法来确定最佳个数。
[1]陈成龙. 基于人工神经网络的油田开发数据分析及预测研究[D].东北石油大学,2022.DOI:10.26995/d.cnki.gdqsc.2022.000046.
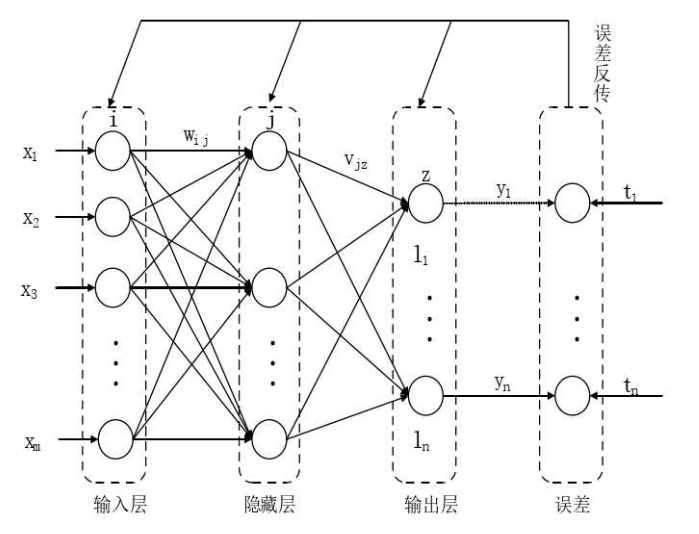
只含1个隐藏层的BP神经网络结构如图所示:
BP神经网络一般采用单隐层结构
隐藏层多,不一定会使得结果更准确,但是,会更加耗时,同时效率会降低。
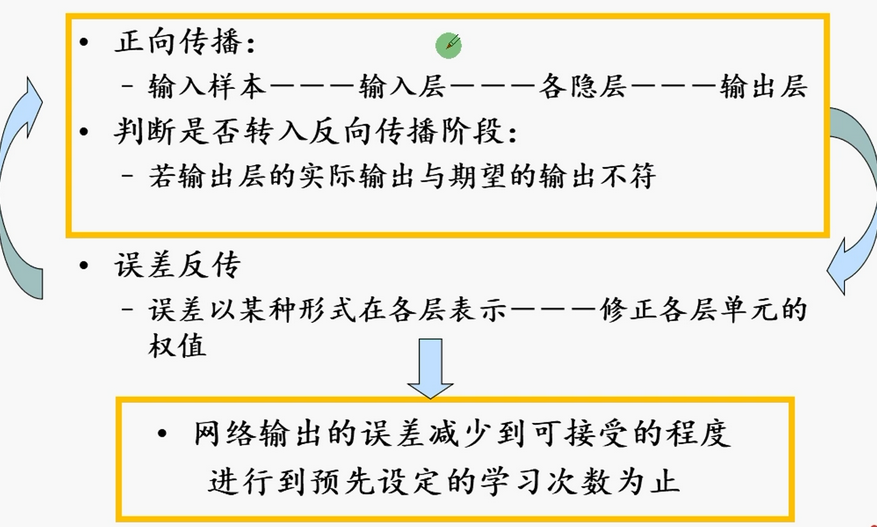
7.4 模型的建立
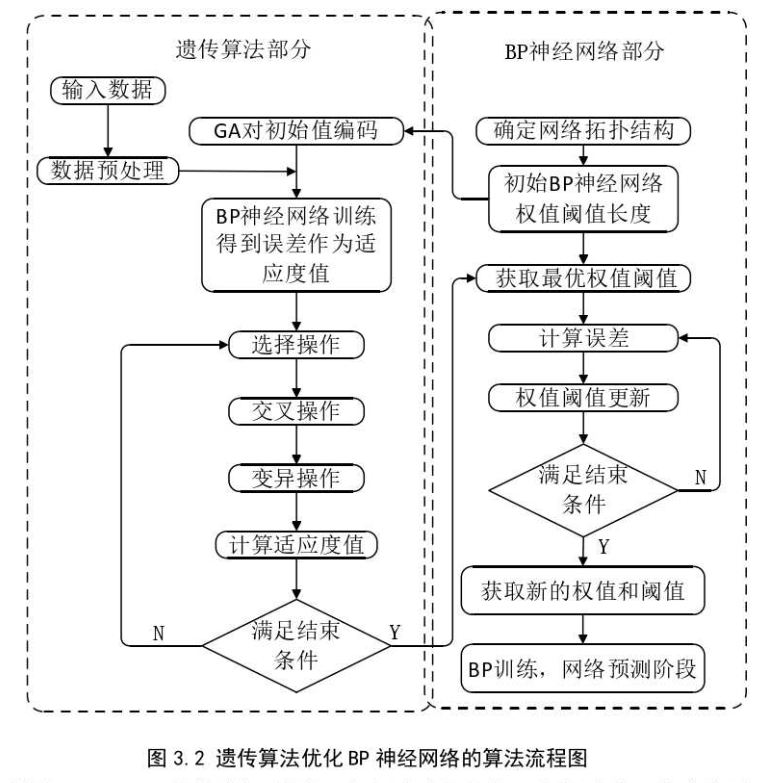
流程图
[1]陈成龙. 基于人工神经网络的油田开发数据分析及预测研究[D].东北石油大学,2022.DOI:10.26995/d.cnki.gdqsc.2022.000046.

一般,p大于n

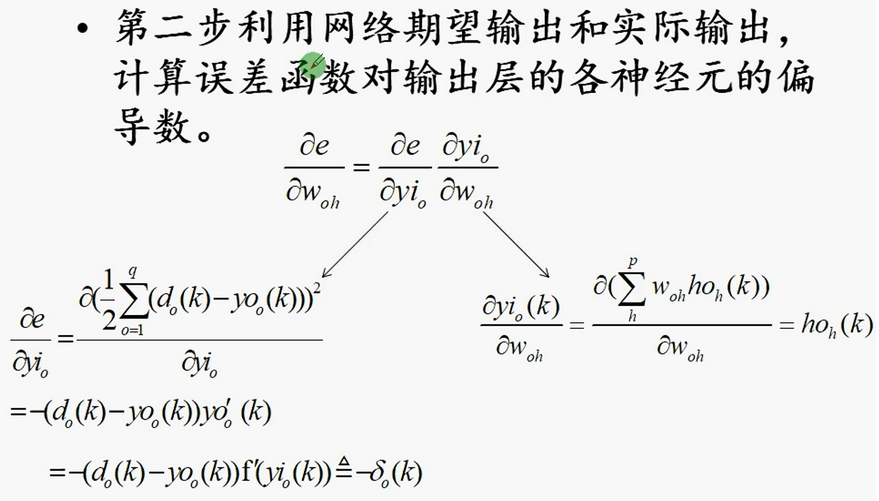

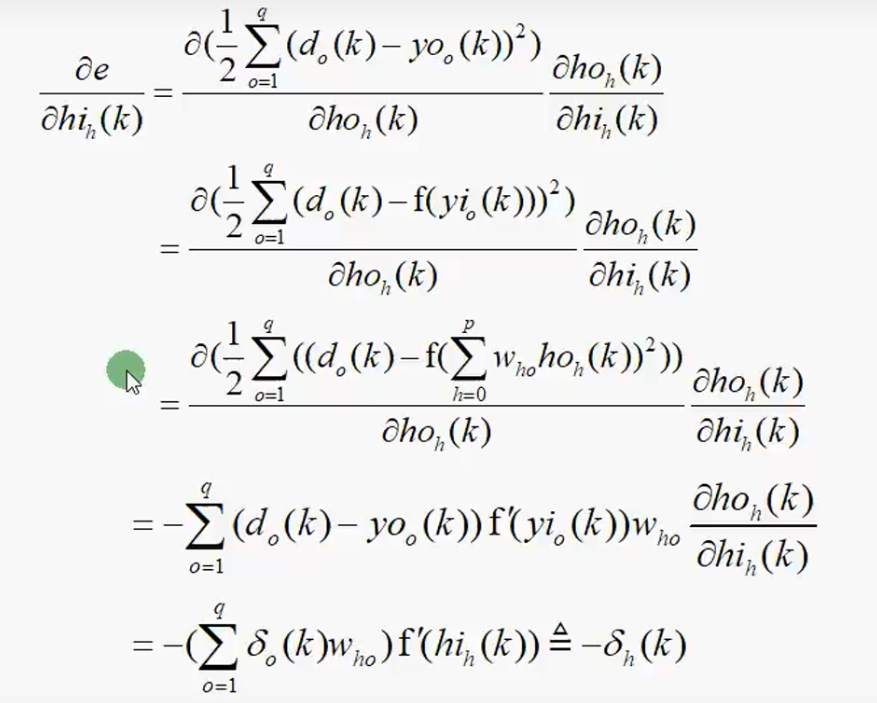

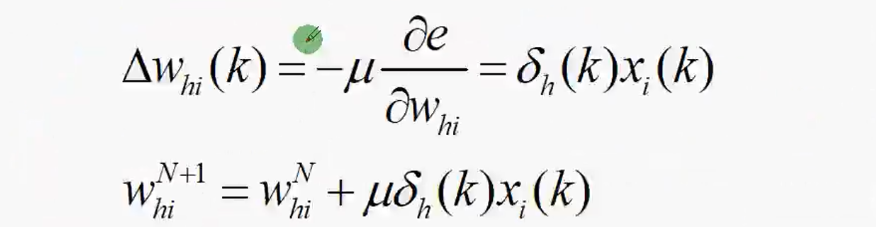
8 神经网络的应用

9 模型的训练

基于拟牛顿算法优化的BP神经网络模型

10 模型建立步骤
- 确定网络拓扑结构
- 即,输入层、隐含层(几层)、输出层的神经元数量
- 符号定义
- 确定初始BP神经网络的权值和阈值
- 更新权值阈值
- 计算各层神经元的输入和输出
- 计算输出层的实际输出和期望输出的误差
- 判断是否满足条件
- 不满足,修正权值
- 更新权值(返回 3)
- 直到误差满足要求或迭代次数达到指定次数


Python数学实验与建模
[1]陈成龙. 基于人工神经网络的油田开发数据分析及预测研究[D].东北石油大学,2022.DOI:10.26995/d.cnki.gdqsc.2022.000046.

