一【题目类别】

• 动态规划

二【题目难度】

• 中等

三【题目编号】

• 45.跳跃游戏 II

四【题目描述】

• 给你一个非负整数数组 nums ，你最初位于数组的第一个位置。
• 数组中的每个元素代表你在该位置可以跳跃的最大长度。
• 你的目标是使用最少的跳跃次数到达数组的最后一个位置。
• 假设你总是可以到达数组的最后一个位置。

五【题目示例】

• 示例 1:

  • 输入: nums = [2,3,1,1,4]
  • 输出: 2
  • 解释: 跳到最后一个位置的最小跳跃数是 2。 从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

• 示例 2:

  • 输入: nums = [2,3,0,1,4]
  • 输出: 2

六【解题思路】

• 利用动态规划的思想
• 要以最短的步数跳到当前位置，要保证前一次也是最短的步数
• 那么只需要找到最短的步数即可
• 所以动态转移方程为：dp[i] = dp[bestIndex] + 1，（其中bestIndex为找到的能走最短步数的下标）
• 最后返回结果即可

七【题目提示】

• $1<=nums.length<=10^4$
• $0<=nums[i]<=1000$

八【时间频度】

• 时间复杂度：$O(n)$，其中 $n$ 是数组长度
• 空间复杂度：$O(n)$，其中 $n$ 是数组长度

九【代码实现】

1. Java语言版

package DynamicProgramming;

public class p45_JumpGameII {

    public static void main(String[] args) {
        int[] nums = {2, 3, 1, 1, 4};
        int res = jump(nums);
        System.out.println("res = " + res);
    }

    public static int jump(int[] nums) {
        int[] dp = new int[nums.length];
        int bestIndex = 0;
        for (int i = 1; i < nums.length; i++) {
            while (i > bestIndex + nums[bestIndex]) {
                bestIndex++;
            }
            dp[i] = dp[bestIndex] + 1;
        }
        return dp[nums.length - 1];
    }

}

2. C语言版

#include<stdio.h>
#include<stdlib.h>

int jump(int* nums, int numsSize)
{
	int* dp = (int*)calloc(numsSize, sizeof(int));
	int bestIndex = 0;
	for (int i = 1; i < numsSize; i++)
	{
		while (i > bestIndex + nums[bestIndex])
		{
			bestIndex++;
		}
		dp[i] = dp[bestIndex] + 1;
	}
	return dp[numsSize - 1];
}

/*主函数省略*/

十【提交结果】

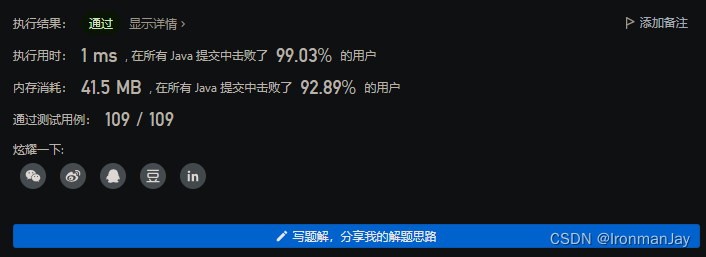
1. Java语言版
   

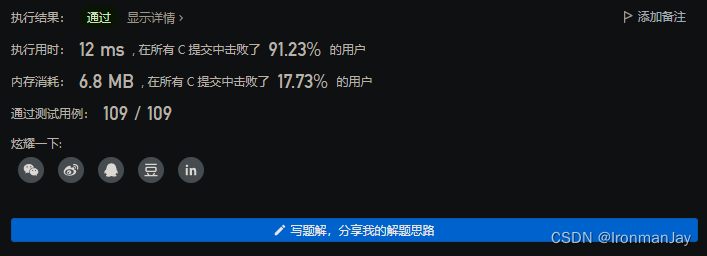
2. C语言版