【深度学习】R-GCN的dgl官方代码解读（entity classification）

来源：r-gcn官方代码实现：4_rgcn.py

以下主要是记录个人对官方代码的理解。注意这篇官方教程只写了entity classification的代码。

参考文章：这篇博客

R-GCN：多层网络

由多层R-GCNLayer组成，代码比较简单在此略过，重点看每一层是怎么实现的。

RGCNLayer：单层卷积网络

先全部摆出来，然后再着重看几个部分。

class RGCNLayer(nn.Module):
    def __init__(self, in_feat, out_feat, num_rels, num_bases=-1, bias=None,
                 activation=None, is_input_layer=False):
        super(RGCNLayer, self).__init__()
        self.in_feat = in_feat  # 输入维度
        self.out_feat = out_feat  # 输出维度
        self.num_rels = num_rels  # 边类型数量（关系数量）  # |E|=num_rels(关系个数、边的种类)
        self.num_bases = num_bases  # W_r分解的数量，对应原文公式3的B
        self.bias = bias  # 偏置，应该和模型输出的维度一样
        self.activation = activation  # 激活函数
        self.is_input_layer = is_input_layer  # 是否是输入层（第一层）

        # sanity check
        # 矩阵分解的参数校验条件：不能小于0，不能比现有维度大（复杂度会变高，参数反而增加）
        if self.num_bases <= 0 or self.num_bases > self.num_rels:
            self.num_bases = self.num_rels

        # weight bases in equation (3)
        # 这里是根据公式3把W_r算出来，用V_b（weight）表示，共有num_bases个V_b累加得到
        # 得到的结果是Tensor，因此用 nn.Parameter将一个不可训练的类型Tensor
        # 转换成可以训练的类型Parameter
        # 并将这个parameter绑定到这个module里面
        self.weight = nn.Parameter(torch.Tensor(self.num_bases, self.in_feat,
                                                self.out_feat))
        if self.num_bases < self.num_rels:  # B < 边种类|E|，那么矩阵分解就可以减少参数个数
            # linear combination coefficients in equation (3)
            # 这里的w_comp是公式3里面的a_{rb}
            # 一个边类型对应一个W_r（那么就一共有num_rels种W_r），每个W_r分解为num_bases个组合
            # 因此w_comp这里的维度就是num_rels×num_bases
            self.w_comp = nn.Parameter(torch.Tensor(self.num_rels, self.num_bases))

        # add bias
        if self.bias:
            self.bias = nn.Parameter(torch.Tensor(out_feat))

        # init trainable parameters
        # 这里用的是xavier初始化
        nn.init.xavier_uniform_(self.weight,
                                gain=nn.init.calculate_gain('relu'))
        if self.num_bases < self.num_rels:
            nn.init.xavier_uniform_(self.w_comp,
                                    gain=nn.init.calculate_gain('relu'))
        if self.bias:
            nn.init.xavier_uniform_(self.bias,
                                    gain=nn.init.calculate_gain('relu'))

    def forward(self, g):
        if self.num_bases < self.num_rels:  # 分解就走公式3：  B<|E|
            # generate all weights from bases (equation (3))
            weight = self.weight.view(self.in_feat, self.num_bases, self.out_feat)
            weight = torch.matmul(self.w_comp, weight).view(self.num_rels,
                                                            self.in_feat, self.out_feat)  
            # |E|=num_rels(关系个数、边的种类)
            # w_comp:|E|*B, weight:in*B*out -> in*|E|*out -> |E|*in*out
        else:  # 不分解就直接用weight算
            weight = self.weight  # |E|*in*out, 此时|E|=B=min{|E|, B}

        if self.is_input_layer:
            def message_func(edges):
                # for input layer, matrix multiply can be converted to be
                # an embedding lookup using source node id
                # 对于第一层，输入可以直接用独热编码进行aggregate
                # 信息的汇聚就可以直接写成矩阵相乘的形式
                embed = weight.view(-1, self.out_feat)  # embed维度整成out_feat维度一样
                index = edges.data['rel_type'] * self.in_feat + edges.src['id']
                return {'msg': embed[index] * edges.data['norm']}
        else:
            def message_func(edges):
                w = weight[edges.data['rel_type'].long()]  # 根据边类型'rel_type'获取对应的
                # 这个切片就有点神奇了，weight是B*in*out，edges.data['rel_type']是(65439,)，切出来是w:65439*in*out
                # 我悟了
                msg = torch.bmm(edges.src['h'].unsqueeze(1), w).squeeze()  # 消息汇聚，就是w乘以src['h']（输入节点特征）
                # edges.src['h'].unsqueeze(1): 65439*in -> 65439*1*in
                # (65439*1*in) * (65439*in*out) -> 65439*1*out 广播，
                # 前一项提出65439，然后1*in与in*out作矩阵乘法，得1*out，然后与65439组合成65439*1*out
                # .squeeze() msg: 65439*1*out -> 65439*out
                msg = msg * edges.data['norm']
                return {'msg': msg}

        def apply_func(nodes):
            h = nodes.data['h']
            if self.bias:
                h = h + self.bias
            if self.activation:
                h = self.activation(h)
            return {'h': h}

        g.update_all(message_func, fn.sum(msg='msg', out='h'), apply_func)

重点讲一下几个变量和函数。

基函数分解

self.w_comp变量

        if self.num_bases < self.num_rels:  # B < 边种类|E|，那么矩阵分解就可以减少参数个数
            # linear combination coefficients in equation (3)
            # 这里的w_comp是公式3里面的a_{rb}
            # 一个边类型对应一个W_r（那么就一共有num_rels种W_r），每个W_r分解为num_bases个组合
            # 因此w_comp这里的维度就是num_rels×num_bases
            self.w_comp = nn.Parameter(torch.Tensor(self.num_rels, self.num_bases))

self.weight变量

        # weight bases in equation (3)
        # 这里是根据公式3把W_r算出来，用V_b（weight）表示，共有num_bases个V_b累加得到
        # 得到的结果是Tensor，因此用 nn.Parameter将一个不可训练的类型Tensor
        # 转换成可以训练的类型Parameter
        # 并将这个parameter绑定到这个module里面
        self.weight = nn.Parameter(torch.Tensor(self.num_bases, self.in_feat,
                                                self.out_feat))

forward函数

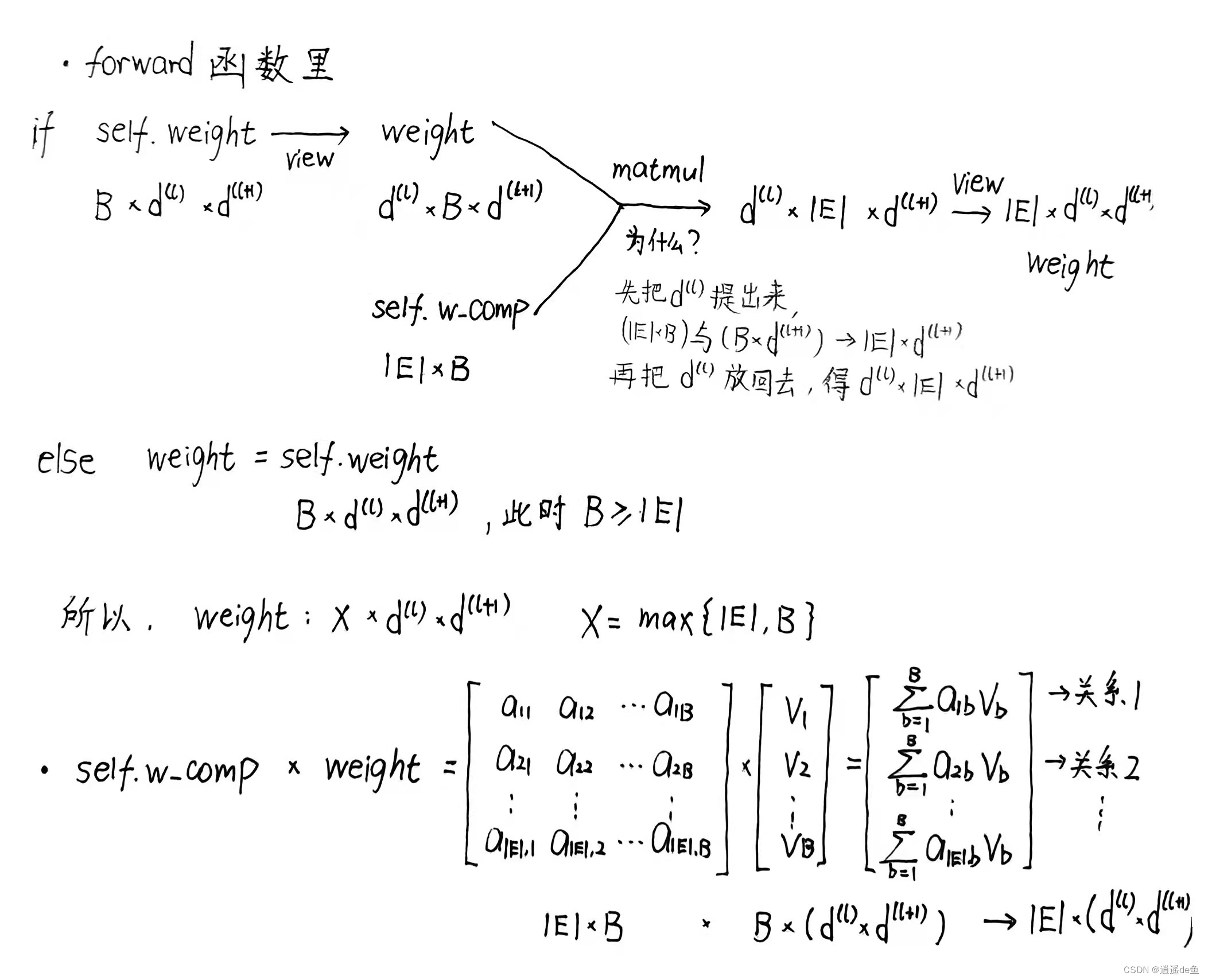
B是人为设定的超参数，如果B小于关系数目（边的种类数目），那么说明我们要用基函数分解，来增加模型约束，减少过拟合；如果B大于等于关系数目，那么基函数分解就没有必要的，反而会增大模型的参数个数。

    def forward(self, g):
        if self.num_bases < self.num_rels:  # 分解就走公式3：  B<|E|
            # generate all weights from bases (equation (3))
            weight = self.weight.view(self.in_feat, self.num_bases, self.out_feat)
            weight = torch.matmul(self.w_comp, weight).view(self.num_rels,
                                                            self.in_feat, self.out_feat)
            # |E|=num_rels(关系个数、边的种类)
            # w_comp:|E|*B, weight:in*B*out -> in*|E|*out -> |E|*in*out
        else:  # 不分解就直接用weight算, B>=|E|
            weight = self.weight  # |E|*in*out, 此时|E|=B=max{|E|, B}

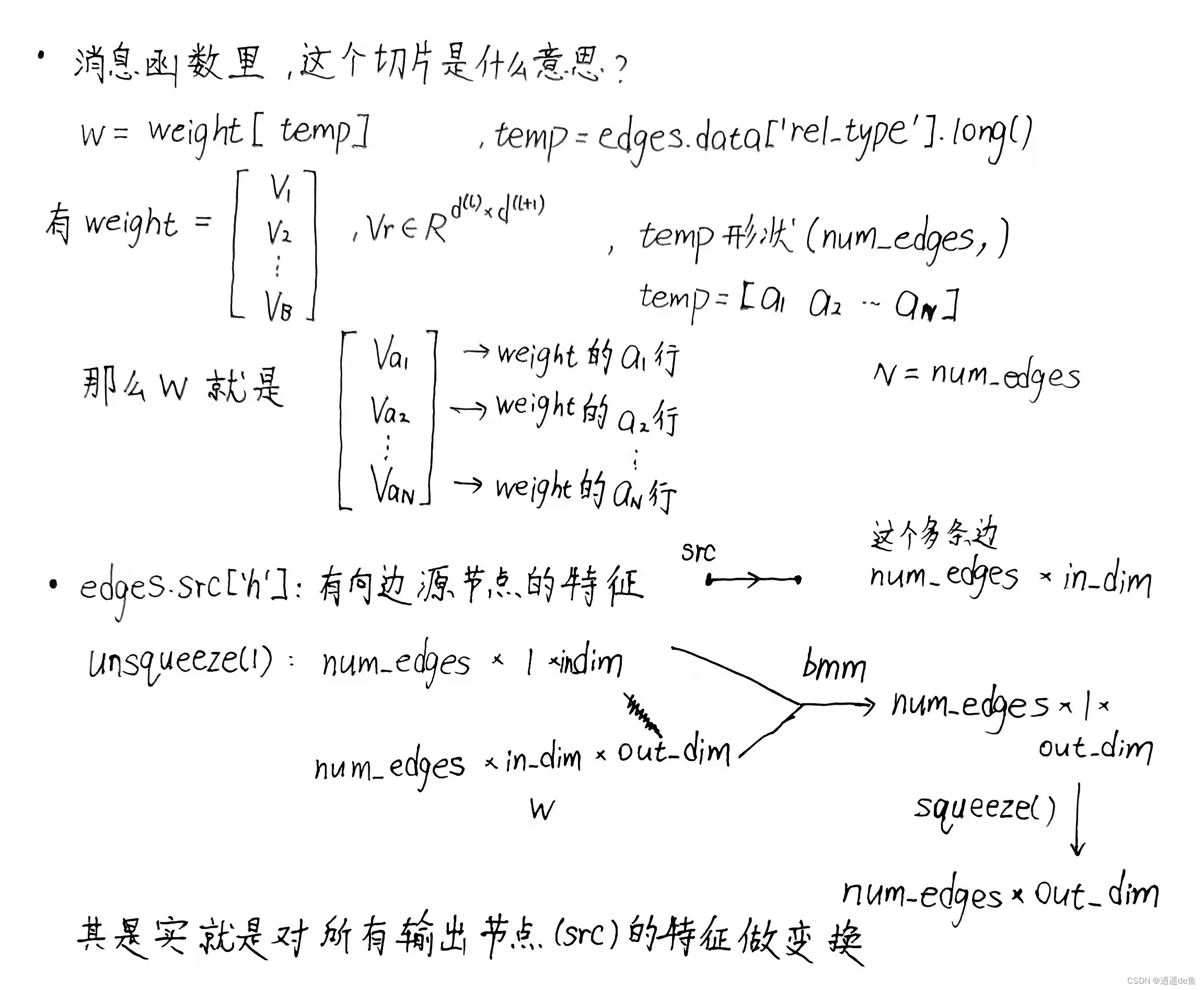
消息函数

            def message_func(edges):
                w = weight[edges.data['rel_type'].long()]  # 根据边类型'rel_type'获取对应的
                # 这个切片就有点神奇了，weight是B*in*out，edges.data['rel_type']是(65439,)，切出来是w:65439*in*out
                # 我悟了
                msg = torch.bmm(edges.src['h'].unsqueeze(1), w).squeeze()  # 消息汇聚，就是w乘以src['h']（输入节点特征）
                # edges.src['h'].unsqueeze(1): 65439*in -> 65439*1*in
                # (65439*1*in) * (65439*in*out) -> 65439*1*out 广播，
                # 前一项提出65439，然后1*in与in*out作矩阵乘法，得1*out，然后与65439组合成65439*1*out
                # .squeeze() msg: 65439*1*out -> 65439*out
                msg = msg * edges.data['norm']
                return {'msg': msg}

https://blog.csdn.net/Wolf_AgOH/article/details/124528026