Linear Regression——线性回归
机械学习——线性回归(Linear Regression)
导入相关库
import numpy as np
from matplotlib import pyplot as plt
#解决中文乱码
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
加载绘图函数
#绘制加载训练集数据
def plot_X(X):
plt.figure()
(n, m) = np.shape(X)
if m == 1:
#一元绘图
plt.plot(X, marker="x", linestyle='')
elif m == 2:
#二元绘图
plt.xlabel("x1")
plt.ylabel("x2")
plt.scatter(X[:,0], X[:, 1])
plt.show()
#绘制损失函数图像
def plotJ(Loss):
plt.figure(figsize=(20, 10))
plt.title("损失loss随迭代次数epoch的变化图")
plt.xlabel("epoch")
plt.ylabel("loss")
plt.plot(range(len(Loss)), Loss)
#最优点
plt.plot(Loss.index(min(Loss)), min(Loss), color="red", marker="x")
plt.text(Loss.index(min(Loss)), min(Loss)+1, s="最优点")
plt.show()
训练样本数据处理
1.加载数据集
数据集存放在data.txt文件中数据如下:
2104,3,399900
1600,3,329900
2400,3,369000
1416,2,232000
3000,4,539900
1985,4,299900
1534,3,314900
1427,3,198999
1380,3,212000
1494,3,242500
1940,4,239999
2000,3,347000
1890,3,329999
4478,5,699900
1268,3,259900
2300,4,449900
1320,2,299900
1236,3,199900
2609,4,499998
3031,4,599000
1767,3,252900
1888,2,255000
1604,3,242900
1962,4,259900
3890,3,573900
1100,3,249900
1458,3,464500
2526,3,469000
2200,3,475000
2637,3,299900
1839,2,349900
1000,1,169900
2040,4,314900
3137,3,579900
1811,4,285900
1437,3,249900
1239,3,229900
2132,4,345000
4215,4,549000
2162,4,287000
1664,2,368500
2238,3,329900
2567,4,314000
1200,3,299000
852,2,179900
1852,4,299900
1203,3,239500
def load_data():
"""
加载数据集:data
"""
data = np.loadtxt(fname="data.txt", delimiter=',', dtype=np.float)
return data
2.数据集分割
将加载的数据集分割为X和Y
def data_split(data):
"""
数据预处理
param: data list 原始数据
return [X_p, Y] X_p list 处理后数据
Y list 对应X_p样本结果集
"""
X_p = data[:,:-1]
Y = data[:, -1]
#绘图
plot_X(X_p)
return [X_p, Y]
3.样本数据向量化
- 样本数据:X为n个特征m个样本
- 编号说明:i ii一般是样本的索引 ;j jj是样本特征指的索引
- 全为1的行为θ \thetaθ对应的偏置项
- 自变量:
X = ( X ( 1 ) X ( 2 ) X ( 3 ) . . . X ( i ) . . . X ( m ) ) = ( 1 1 1 . . 1 . . . 1 x 1 ( 1 ) x 1 ( 2 ) x 1 ( 3 ) . . x 1 ( i ) . . . x 1 ( m ) x 2 ( 1 ) x 2 ( 2 ) x 2 ( 3 ) . . . x 2 ( i ) . . . x 2 ( m ) x 3 ( 1 ) x 3 ( 2 ) x 3 ( 3 ) . . x 3 ( i ) . . . x 3 ( m ) . . . . . . . . . . . . . . . . . . . . . . . . x j ( i ) . . . . . . . . . . . . . . . . . . . . . . . x n ( 1 ) x n ( 2 ) x n ( 3 ) . . x n ( i ) . . . x n ( m ) ) ( n + 1 ) × m (1) X = \left( \begin{matrix} X^{(1)} & X^{(2)} & X^{(3)} & ... & X^{(i)}...& X^{(m)}\\ \end{matrix} \right)= \left( \begin{matrix} 1 & 1 & 1 & .. & 1 &... & 1\\ x_{1}^{(1)} & x_{1}^{(2)} & x_{1}^{(3)} & .. & x_{1}^{(i)} &... & x_{1}^{(m)}\\ x_{2}^{(1)} & x_{2}^{(2)} & x_{2}^{(3)} & ...& x_{2}^{(i)} &...& x_{2}^{(m)}\\ x_{3}^{(1)} & x_{3}^{(2)} & x_{3}^{(3)} & ..& x_{3}^{(i)} &...& x_{3}^{(m)}\\ .. & .. & ..&..&.. &...& ...\\ .. & .. & ..&..&x_{j}^{(i)} &... & ...\\ .. & .. & ..&..&.. &...& ....\\ x_{n}^{(1)} & x_{n}^{(2)} & x_{n}^{(3)} & ..& x_{n}^{(i)} &...& x_{n}^{(m)}\\ \end{matrix} \right)_{(n+1) \times m } \tag{1}X=(X(1)X(2)X(3)...X(i)...X(m))=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛1x1(1)x2(1)x3(1)......xn(1)1x1(2)x2(2)x3(2)......xn(2)1x1(3)x2(3)x3(3)......xn(3).................1x1(i)x2(i)x3(i)..xj(i)..xn(i)........................1x1(m)x2(m)x3(m)..........xn(m)⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞(n+1)×m(1)
- 因变量:
Y = ( y ( 1 ) y ( 2 ) y ( 3 ) . . y ( i ) . . . y ( m ) ) m × 1 T (2) Y = \left( \begin{matrix} y^{(1)} & y^{(2)} & y^{(3)} & ..& y^{(i)} & ... & y^{(m)} \\ \end{matrix} \right)_{m \times 1}^{T} \tag{2}Y=(y(1)y(2)y(3)..y(i)...y(m))m×1T(2)
def matrix(X_nor):
"""
训练样本向量化
param: X_nor list 归一化后的训练样本数据
return: X list 训练样本向量化数据
"""
(n,m) = np.shape(X_nor)
ones = np.ones((n,1))
X = np.hstack((ones, X_nor))
return X.T
4.样本数据归一化
- 归一化目的:减少数据大小,消除量纲影响,减少参数重要性,加快收敛速度,提高模型精度【提高特征之间的比较性(关联性)】
预测的时候也要将数测数据进行归一化处理,再进行预测。对X进行归一化处理,特征之间的关联性,让特征均有0的均值
- 由于代价函数计算的时候可能会出现指数式爆炸性增长,导致内存溢出。所以采用将训练样本归一化的处理方法,将输入数据归一化到[0, 1]之间。
- 注意:归一化的对象应是同指标(特征)数据的归一化!!!即(1)式中每一行数据X [ j ] X[j]X[j]
- 归一化方法:
- min-max标准化:使用除0均值标准化的场景,比如图像处理中将将值限定在0-255之间
X n o r m = X − X m i n X m a x − X m i n X_{norm}= \frac{X - X_{min}}{X_{max} - X_{min}}Xnorm=Xmax−XminX−Xmin - 0均值标准化:推荐,适用于1分类,聚类算法,需要用距离来度量相似性,PCA降维
- min-max标准化:使用除0均值标准化的场景,比如图像处理中将将值限定在0-255之间
要求原数据近似高斯分布(正态分布),将原始数据集归一化为均值为0,方差为1的数据集
z = x − μ σ z = \frac{x - \mu}{\sigma}z=σx−μ
μ \muμ ——均值
σ \sigmaσ ——标准差
def normal(X):
"""
采用0均值归一化,仅需要对特征X进行归一化处理
param: X list 训练样本数据 每列为一个特征
return:
X_nor list 归一化化后的数据
average list X每列计算的均值
variance list X每列计算的方差
"""
#计算均值 #axis=0 按列 axis=1 按行
average = np.mean(X, axis=0)
# print(average)
#计算方差
variance = np.std(X, axis=0)
# print(variance)
(n, m) = np.shape(X)
X_nor = np.ones((n, 1))
for i in range(m):
tmp = (np.array(X[:, i]) - average[i]) / variance[i]
X_nor = np.hstack((X_nor, tmp.reshape((-1, 1))))
X_nor = X_nor[:, 1:]
return [X_nor, average, variance]
数据预处理函数封装
#数据预处理
def data_dispose(data):
"""
数据预处理函数
param: data 数据集(一定格式的数据集)
retrun: X 向量化后的样本数据集
Y X对应的结果集
average list X每列计算的均值
variance list X每列计算的方差
"""
#数据集分割
[X_p, Y] = data_split(data)
#特征归一化
[X_nor, average, variance] = normal(X_p)
#样本向量化
X = matrix(X_nor)
return [X, Y, average, variance]
假设函数
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + . . . + θ j x j + . . . + θ n x n h_{\theta}(x) = \theta_{0} + \theta_{1} x_{1}+ \theta_{2} x_{2}+ \theta_{3} x_{3}+...+\theta_{j} x_{j}+...+\theta_{n} x_{n}hθ(x)=θ0+θ1x1+θ2x2+θ3x3+...+θjxj+...+θnxn
- 模型参数:及我们所要训练数据集所要求解的
Θ = ( θ 0 θ 1 θ 2 θ 3 . . θ j . . . θ n ) n × 1 T (3) \Theta = \left( \begin{matrix} \theta_{0} &\theta_{1} & \theta_{2} & \theta_{3} & .. &\theta_{j}... & \theta_{n}\\ \end{matrix} \right)_{n \times 1}^{T} \tag{3}Θ=(θ0θ1θ2θ3..θj...θn)n×1T(3)
代价函数
- 代价即预测模型求解h与真实值y之间的差距,这里的差距一般以数值差值来衡量代价值

- 目标:使代价值越小越好
- 方法:gradient descent ——梯度下降
- 代价函数表达式:关于Θ \ThetaΘ的函数
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta) =\frac{1}{2m}\sum_{i=1}^{m}( h_{\theta}(x^{(i)})- y^{(i)})^{2}J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
其中h θ ( x ( i ) ) = θ 0 + θ 1 x 1 ( i ) + θ 2 x 2 ( i ) + θ 3 x 3 ( i ) + . . . + θ j x j ( i ) + . . . + θ n x n ( i ) h_{\theta}(x^{(i)}) = \theta_{0} + \theta_{1} x_{1}^{(i)} +\theta_{2} x_{2}^{(i)} +\theta_{3} x_{3}^{(i)} +...+\theta_{j} x_{j}^{(i)} +...+\theta_{n} x_{n}^{(i)}hθ(x(i))=θ0+θ1x1(i)+θ2x2(i)+θ3x3(i)+...+θjxj(i)+...+θnxn(i)
代价函数除以样本总量m是为了用平均代价来衡量总样本代价,除以2是为了求导时候便于计算消去2.
- 编号说明:i ii一般是样本的索引 ;j jj是样本特征指的索引
初始化模型参数Θ \ThetaΘ
- 利用gradient descent梯度下降更新参数θ j \theta_{j}θj之前需要初始化参数θ \thetaθ值,由于初始化θ \thetaθ值会影响收敛速度和效果,过于复杂,这里为了简单统一初始化为0,默认从原点开始找:
Θ = ( 0 0 0 0 . . 0... 0 ) n × 1 T \Theta = \left( \begin{matrix} 0 &0 & 0 & 0 & .. &0... & 0\\ \end{matrix} \right)_{n \times 1}^{T}Θ=(0000..0...0)n×1T
def init_theta(X):
"""
初始化模型参数theta
param: X 样本向量化特征集
"""
(n, m) = np.shape(X)
# 初始化theta 为列向量
theta = np.zeros((n,1),dtype=np.float)
return theta
学习率的选择
关于学习率的选取,比较复杂深入,有兴趣自己可以百度有关学习率选取的文章。通常学习率选取0.01,0.1,0.030.3 等3的倍数,常取0.01.
注意:如果学习率过小,计算量会增大,迭代次数也会增加。如果学习率过大,则可能迭代最优解会会在真正最优解两边来回跳跃,从而达不到最优点。
def choose_lr():
"""
选择学习率
"""
lr = 0.01
return lr
梯度下降
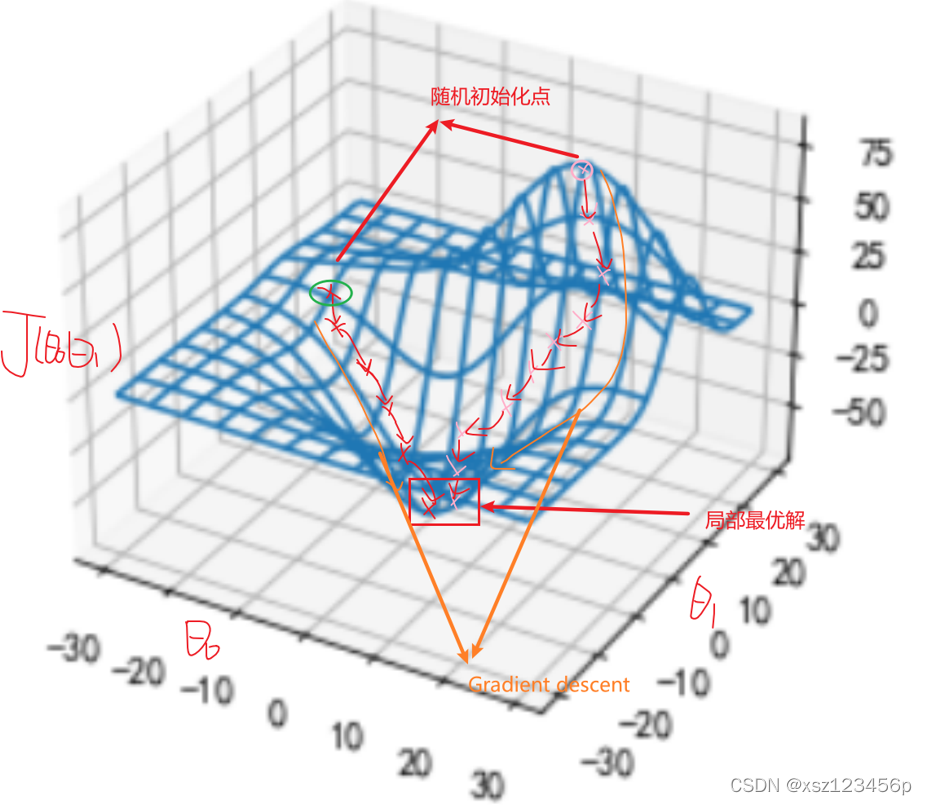
- 模型参数Θ = ( θ 0 θ 1 θ 2 θ 3 . . θ j . . . θ n ) T \Theta = \left( \begin{matrix} \theta_{0} &\theta_{1} & \theta_{2} & \theta_{3} & .. &\theta_{j}... & \theta_{n}\\ \end{matrix} \right)^{T}Θ=(θ0θ1θ2θ3..θj...θn)T
- θ \thetaθ更新公式:
θ j : = θ j − α ∂ J ( Θ ) ∂ θ j \theta_{j} := \theta_{j} - \alpha \frac{ \partial J(\Theta)}{\partial \theta_{j}}θj:=θj−α∂θj∂J(Θ)
α \alphaα——learning rate学习率:一般取0.01, 0.1, 0.03, 0.3等3的倍数。有相关优化α \alphaα的算法,有兴趣可以自行了解,这里统一为α = 0.01 \alpha=0.01α=0.01
更新实现方法
利用循环遍历更新方式——逐个更新
 > 这里引入临时变量说是由于当第一个参数更新以后,如果直接赋值给本身则会影响关于θ \thetaθ的J ( θ ) J(\theta)J(θ)函数,导致该点位置发生变化,如果用于更新下一个点则会是下个点的偏导,而非上个迭代点的偏导。
> 这里引入临时变量说是由于当第一个参数更新以后,如果直接赋值给本身则会影响关于θ \thetaθ的J ( θ ) J(\theta)J(θ)函数,导致该点位置发生变化,如果用于更新下一个点则会是下个点的偏导,而非上个迭代点的偏导。利用矩阵更新(同时更新):推荐
Θ = ( θ 0 θ 1 θ 2 θ 3 . . θ j . . . θ n ) = Θ − α ∂ J ( Θ ) ∂ Θ \Theta = \left( \begin{matrix} \theta_{0} &\theta_{1} & \theta_{2} & \theta_{3} & .. &\theta_{j}... & \theta_{n}\\ \end{matrix} \right)=\Theta-\alpha\frac{\partial J(\Theta)}{\partial\Theta}Θ=(θ0θ1θ2θ3..θj...θn)=Θ−α∂Θ∂J(Θ)
求解梯度:
∂ J ( Θ ) ∂ θ j = 1 m ∑ i = 1 m [ ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ] \frac{\partial J(\Theta)}{\partial \theta_{j}} = \frac{1}{m}\sum_{i=1}^{m} [( h_{\theta}(x^{(i)})-y^{(i)}) x^{(i)}_{j}]∂θj∂J(Θ)=m1i=1∑m[(hθ(x(i))−y(i))xj(i)]推导过程
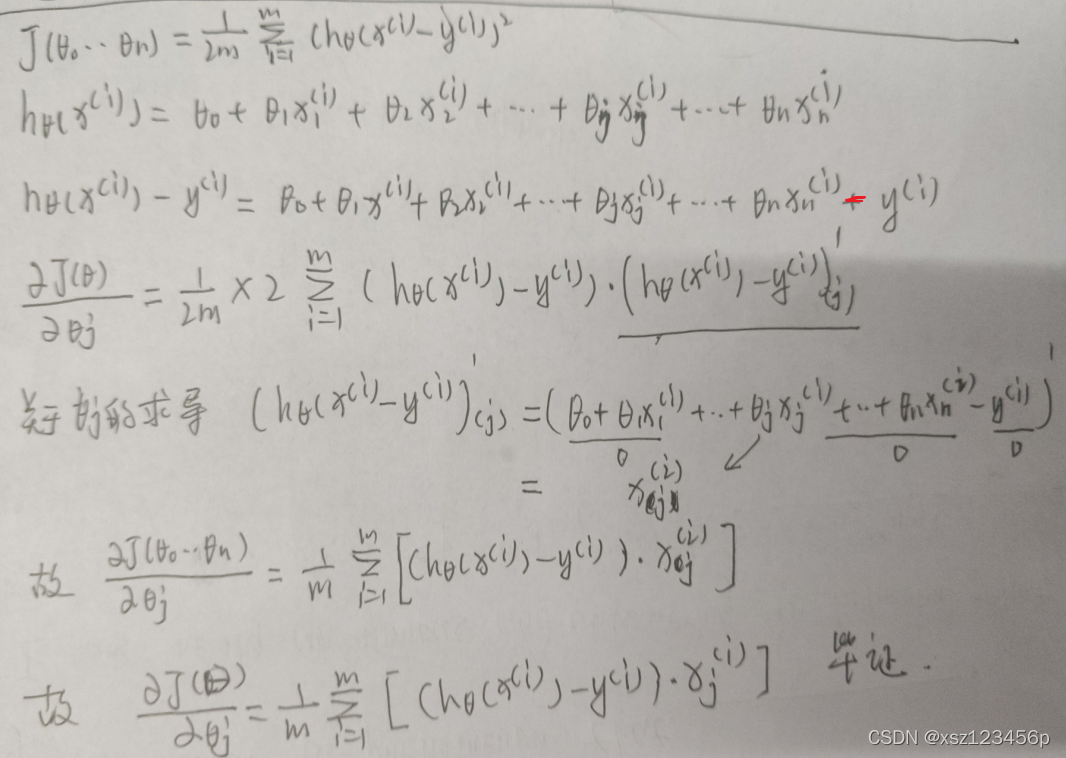
暂时省略代码,推荐用向量化样本的方法计算梯度向量化更新:推荐
Θ = ( θ 0 θ 1 θ 2 θ 3 . . θ j . . . θ n ) T = Θ − α ( X @ E R R O R ) \Theta= \left( \begin{matrix} \theta_{0} &\theta_{1} & \theta_{2} & \theta_{3} & .. &\theta_{j}... & \theta_{n}\\ \end{matrix} \right)^{T}=\Theta- \alpha (X @ ERROR)Θ=(θ0θ1θ2θ3..θj...θn)T=Θ−α(X@ERROR)
其中
E R R O R = [ h θ ( x ( 1 ) ) − y ( 1 ) h θ ( x ( 2 ) ) − y ( 2 ) h θ ( x ( 3 ) ) − y ( 3 ) . . . h θ ( x ( i ) ) − y ( i ) . . . h θ ( x ( m ) ) − y ( m ) ] m × 1 = X T @ Θ − Y ERROR = \left[ \begin{matrix} h_{\theta}(x^{(1)})- y^{(1)} \\ h_{\theta}(x^{(2)})- y^{(2)} \\ h_{\theta}(x^{(3)})- y^{(3)} \\ ...\\ h_{\theta}(x^{(i)})- y^{(i)} \\ ... \\ h_{\theta}(x^{(m)})- y^{(m)} \\ \end{matrix} \right]_{m \times 1} =X^{T}@\Theta- YERROR=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡hθ(x(1))−y(1)hθ(x(2))−y(2)hθ(x(3))−y(3)...hθ(x(i))−y(i)...hθ(x(m))−y(m)⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤m×1=XT@Θ−Y
@ 表示矩阵的乘法运算
def train_LinearRegression_model( Theta, X, Y, epoch=10000, learn_rate=0.01):
"""
训练线性回归模型
param: learn_rate float 学习率 默认0.01
epoch int 迭代次数 默认迭代10000次
Theta list 初始化模型参数
X array 向量化样本数据集(训练集)
Y list 训练集X对应的结果集Y
return: Theta list 最优模型参数
Loss list 迭代的样本总损失
"""
#存储所有Theta值
THeta = []
# 样本总损失
Loss = []
for n in range(epoch):
# Error 样本损失
Error = X.T @ Theta - np.reshape(Y, (-1, 1))
# Theta 参数更新
Theta = Theta - learn_rate * (X @ Error)
#存放Theta值
THeta.append(Theta)
# 计算总损失 Lose
Loss.append(np.sum(Error**2) / (2*len(Y)))
#防止由于learn_rate过大导致越过最优点
c = Loss.index(min(Loss))
optim_theta = THeta[c]
return [optim_theta, Loss]
完整代码
import numpy as np
from matplotlib import pyplot as plt
#解决中文乱码
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
#加载数据集
def load_data():
"""
加载数据集:data
"""
data = np.loadtxt(fname="data.txt", delimiter=',', dtype=np.float)
return data
#数据集分割
def data_split(data):
"""
数据预处理
param: data list 原始数据
return [X_p, Y] X_p list 处理后数据
Y list 对应X_p样本结果集
"""
X_p = data[:,:-1]
Y = data[:, -1]
#绘图
plot_X(X_p)
return [X_p, Y]
#归一化处理
def normal(X):
"""
采用0均值归一化,仅需要对特征X进行归一化处理
param: X list 训练样本数据 每列为一个特征
return:
X_nor list 归一化化后的数据
average list X每列计算的均值
variance list X每列计算的方差
"""
#计算均值 #axis=0 按列 axis=1 按行
average = np.mean(X, axis=0)
# print(average)
#计算方差
variance = np.std(X, axis=0)
# print(variance)
(n, m) = np.shape(X)
X_nor = np.ones((n, 1))
for i in range(m):
tmp = (np.array(X[:, i]) - average[i]) / variance[i]
X_nor = np.hstack((X_nor, tmp.reshape((-1, 1))))
X_nor = X_nor[:, 1:]
return [X_nor, average, variance]
#样本向量化
def matrix(X_nor):
"""
训练样本向量化
param: X_nor list 归一化后的训练样本数据
return: X list 训练样本向量化数据
"""
(n,m) = np.shape(X_nor)
ones = np.ones((n,1))
X = np.hstack((ones, X_nor))
return X.T
#数据预处理
def data_dispose(data):
"""
数据预处理函数
param: data 数据集(一定格式的数据集)
retrun: X 向量化后的样本数据集
Y X对应的结果集
average list X每列计算的均值
variance list X每列计算的方差
"""
#数据集分割
[X_p, Y] = data_split(data)
#特征归一化
[X_nor, average, variance] = normal(X_p)
#样本向量化
X = matrix(X_nor)
return [X, Y, average, variance]
#初始化模型参数 Θ
def init_theta(X):
"""
初始化模型参数theta
param: X 样本向量化特征集
"""
(n, m) = np.shape(X)
# 初始化theta 为列向量
theta = np.zeros((n,1),dtype=np.float)
return theta
#学习率的选择
def choose_lr():
"""
选择学习率
"""
lr = 0.01
return lr
#模型训练
def train_LinearRegression_model( Theta, X, Y, epoch=10000, learn_rate=0.01):
"""
训练线性回归模型
param: learn_rate float 学习率 默认0.01
epoch int 迭代次数 默认迭代10000次
Theta list 初始化模型参数
X array 向量化样本数据集(训练集)
Y list 训练集X对应的结果集Y
return: Theta list 最优模型参数
Loss list 迭代的样本总损失
"""
#存储所有Theta值
THeta = []
# 样本总损失
Loss = []
for n in range(epoch):
# Error 样本损失
Error = X.T @ Theta - np.reshape(Y, (-1, 1))
# Theta 参数更新
Theta = Theta - learn_rate * (X @ Error)
#存放Theta值
THeta.append(Theta)
# 计算总损失 Lose
Loss.append(np.sum(Error**2) / (2*len(Y)))
#防止由于learn_rate过大导致越过最优点
c = Loss.index(min(Loss))
optim_theta = THeta[c]
return [optim_theta, Loss]
#模型预测
def predict(x, Theta, average, variance):
"""
模型预测
param: x list 预测数据集(行向量)
Theta list 模型参数
average list 训练数据归一化均值
variance list 训练数据归一化方差
"""
x = np.array(x)
average = np.array(average)
variance = np.array(variance)
# 预测数据归一化处理
x = (x - average) / variance
# 添加偏置系数1
X = np.hstack(([1],x))
# 模型预测
y = X @ Theta
print("预测结果y={0}".format(y))
#绘制特征图
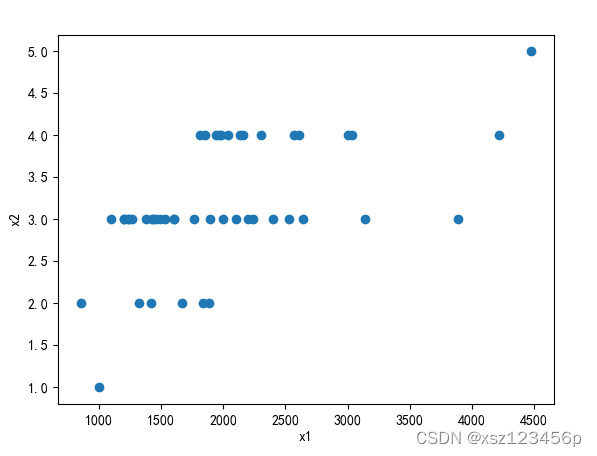
def plot_X(X):
plt.figure()
(n, m) = np.shape(X)
if m == 1:
#一元绘图
plt.plot(X, marker="x", linestyle='')
elif m == 2:
#二元绘图
plt.xlabel("x1")
plt.ylabel("x2")
plt.scatter(X[:,0], X[:, 1])
plt.show()
#绘制损失曲线
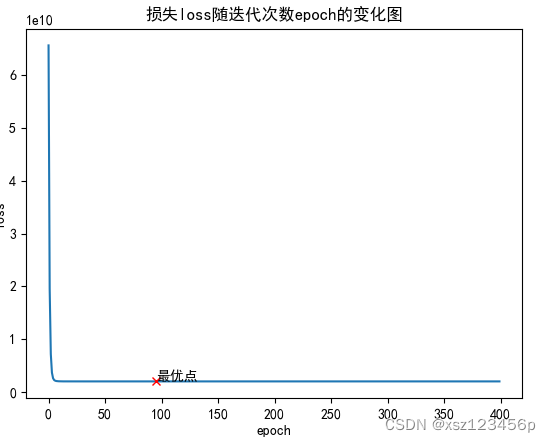
def plotJ(Loss):
plt.figure(figsize=(20, 10))
plt.title("损失loss随迭代次数epoch的变化图")
plt.xlabel("epoch")
plt.ylabel("loss")
plt.plot(range(len(Loss)), Loss)
#最优点
plt.plot(Loss.index(min(Loss)), min(Loss), color="red", marker="x")
plt.text(Loss.index(min(Loss)), min(Loss)+1, s="最优点")
plt.show()
#主程序
if __name__ == "__main__":
#加载数据集
data = load_data()
#数据处理
[X, Y, average, variance] = data_dispose(data)
#初始化模型参数
Theta = init_theta(X)
#选择学习率
learn_rate = choose_lr()
#模型训练
[Theta, Loss] = train_LinearRegression_model(Theta, X, Y,epoch=400, learn_rate=learn_rate)
print("Theta={0}".format(Theta))
#绘制损失图像
plotJ(Loss)
#模型预测
x = [7]
predict(x, Theta, average, variance)
运行结果

说明:该模型适用于一元或多元特征的数据集,只需要将对应data.txt数据按照指定格式保存和修改对应预测的数据运行改程序即可。