Paper地址:https://arxiv.org/abs/1902.08153
GitHub地址 (PyTorch):GitHub - zhutmost/lsq-net: Unofficial implementation of LSQ-Net, a neural network quantization framework
基本量化设置
- 计算结点伪量化:
- Weight跟Activation都采用Per-tensor量化;
- Scaling factor (Paper标记为Step size)作为量化参数,是可训练变量;
- 另外,针对TensorRT、MNN等推理引擎,Weight通常执行Per-channel量化,Activation执行Per-tensor量化;为了加快量化训练收敛,Activation的量化参数(可训练)可借助KL量化、或PyTorch observer量化予以初始化,Weight的量化参数则根据absmax方法在线更新;
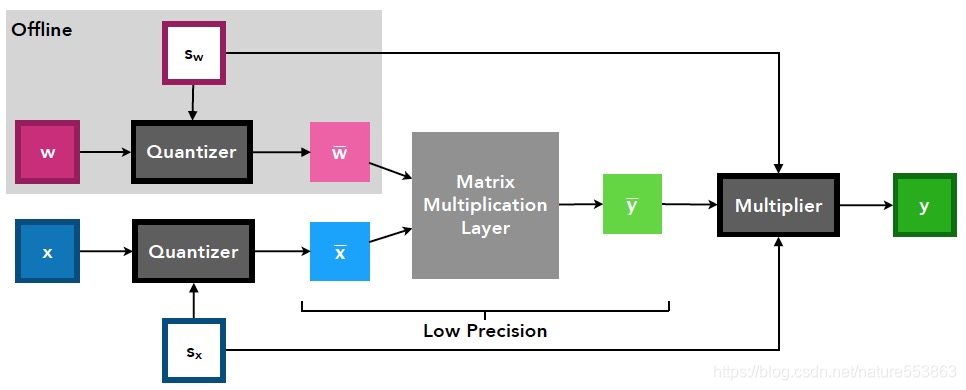
- 量化计算公式:
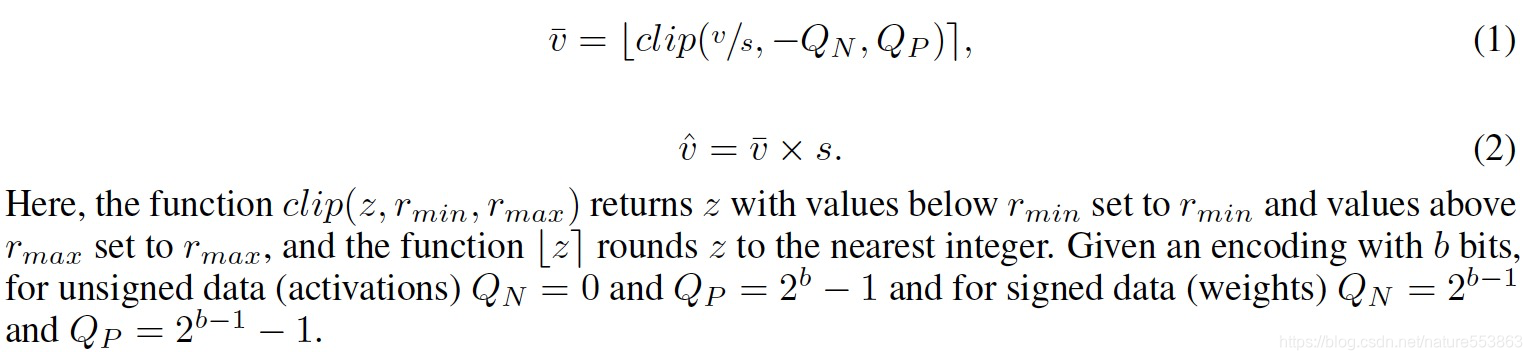
Step-size梯度求解
- Loss关于step-size的梯度推导:
![]()
- 基于STE (Straight Through Estimate),直接Bypass掉Round结点的梯度反传(直接近似):
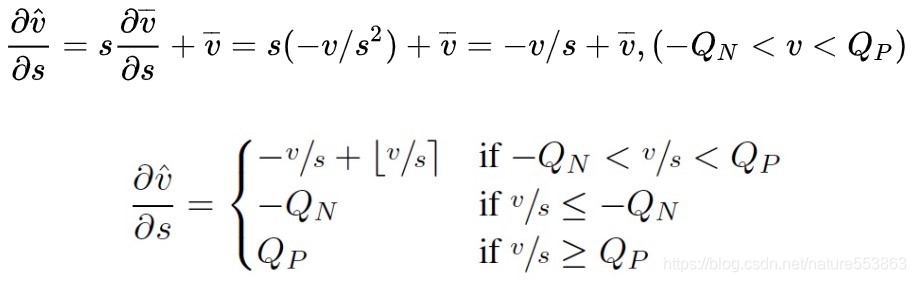
- 与其他方法梯度函数的对比:
- QIL:https://arxiv.org/abs/1808.05779
- PACT:https://arxiv.org/abs/1805.06085
- 相比较而言,LSQ无论在不同Bin之间的Transition位置、还是量化范围的Clip位置,都有较明显的梯度数值,因而更有利Step-size的参数更新:
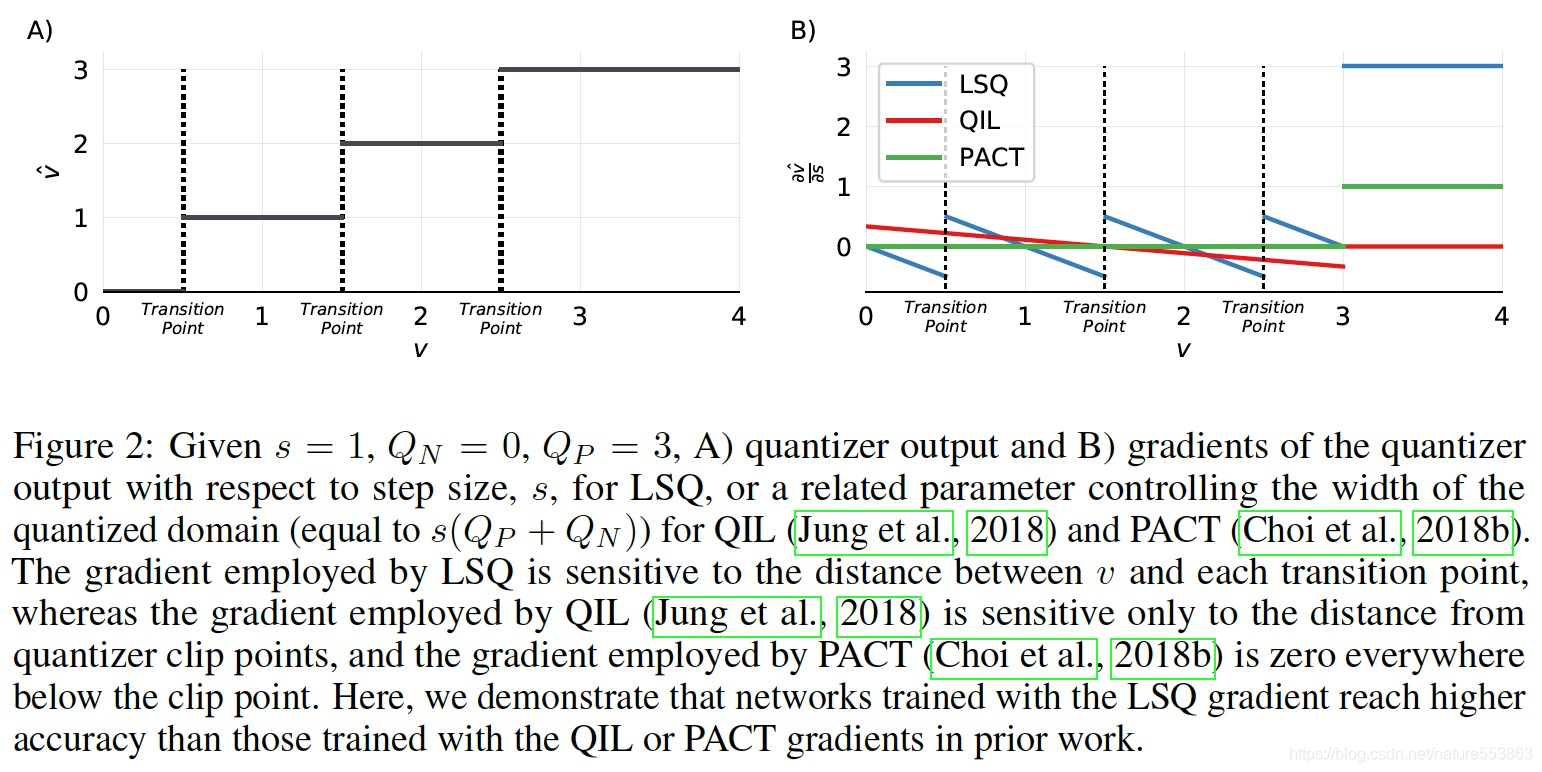
- 梯度的scale:
- 当量化比特数增加时,step-size会变小,以确保更为精细的量化;而当量化比特数减少时,step-size会变大。为了让step-size的参数更新,能够适应量化比特数的调整,需要将step-size的梯度乘以一个scale系数,例如针对weight:
![]()
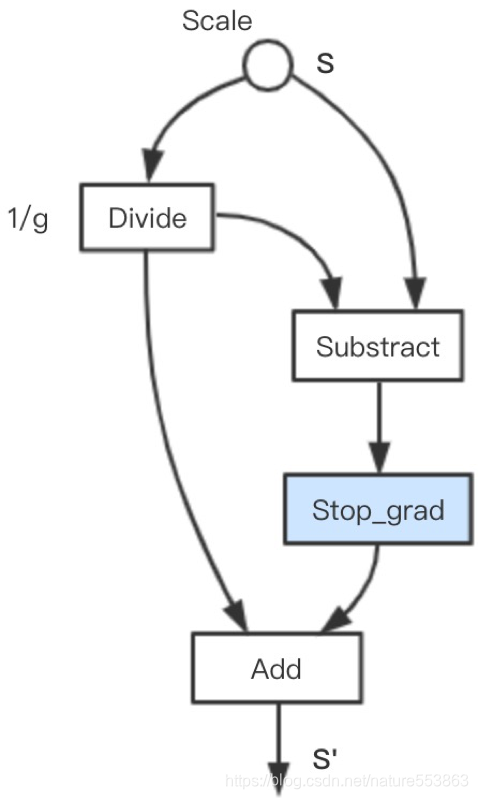
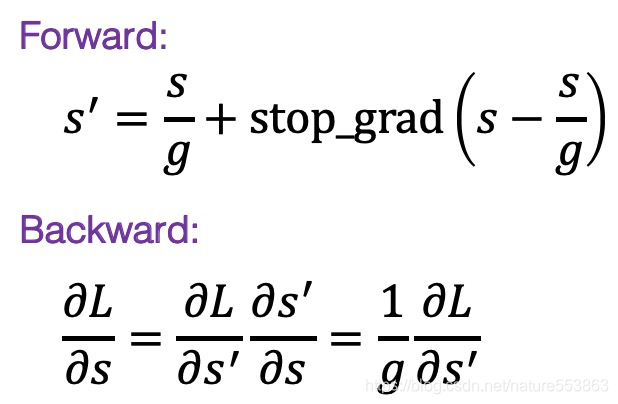
- 再奉上TensorFlow版本的LSQ子图构造代码:
def lsq_grad_scale(inputs, scale_var, max_value=127.0):
"""Gradient scale computation for LSQ."""
tensor_shape = array_ops.shape(inputs)[1:]
grad_scale = (
math_ops.sqrt(
math_ops.cast(math_ops.reduce_prod(tensor_shape), dtypes.float32)
* max_value
)
/ self._grad_scale
)
grad_scale = array_ops.stop_gradient(grad_scale)
# stop gradient backward
scale_div = math_ops.divide(scale_var, grad_scale)
scale_diff = array_ops.stop_gradient(scale_var - scale_div)
step_size = scale_diff + scale_div
return step_size量化训练
- 伪量化训练时,从预训练模型加载FP32参数,学习率按余弦曲线衰减;通常第一层与最后一层固定为INT8量化,有些实际应用场景中亦可固定为FP32(量化敏感层)。
实验结果
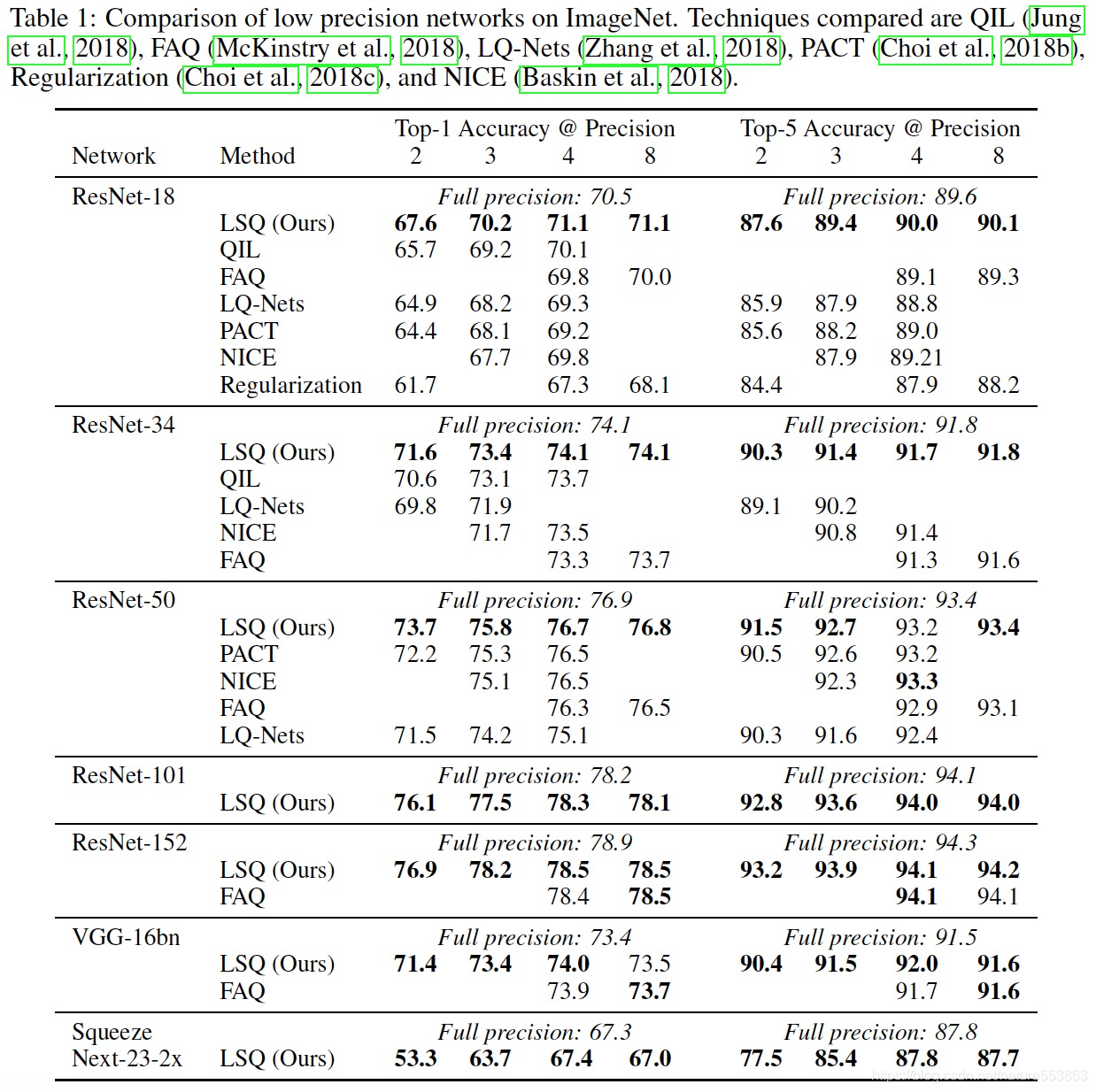
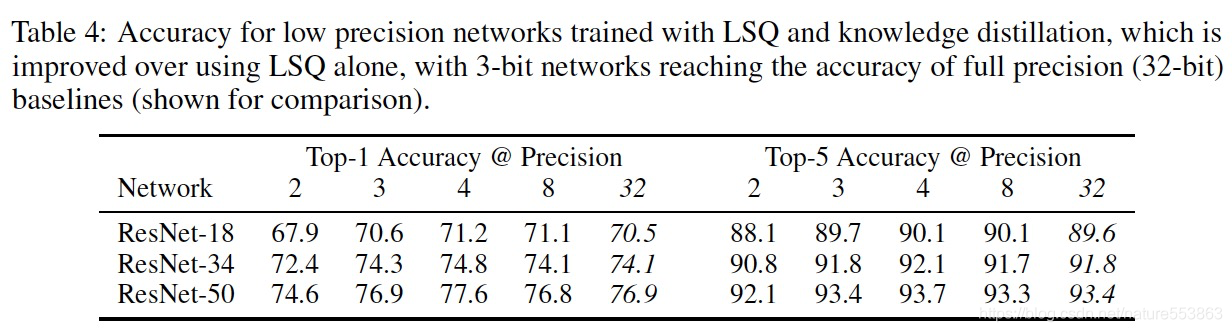
版权声明:本文为nature553863原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。