前言
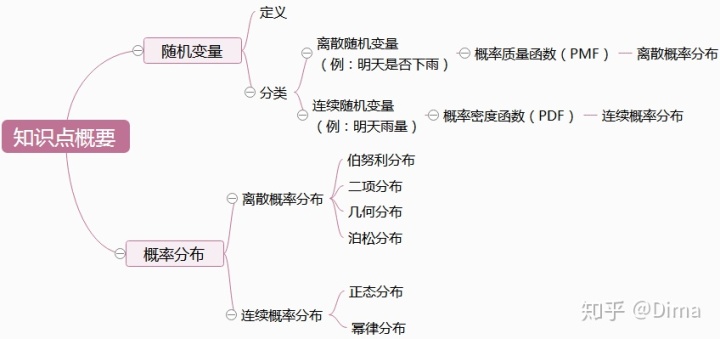
一、随机变量
(一)概念
在统计概率中,用事件来表示某件事情,在一定条件下,可能发生也可能不发生的事件,我们称为随机事件。随机变量是用来量化随机事件的函数,它将随机事件每一个可能的试验结果赋于一个数值。随机变量通常用X、Y等大写字母表示。
例如:明天是否下雨这个随机事件,则可定义随机变量。下雨就等于1,不下雨就等于0(根据需要定义函数值,不一定是0、1),这样,随机变量即将随机事件的结果映射到定义好的数值。又因为明天是否下雨是随机的,即随机变量可取定义好的一个值。
(二)分类
随机变量可分为:离散随机变量 和 连续随机变量。
离散随机变量:即 结果可一一列举出来,也可以说是从一个数字到另一个数字,中间有一定间隔。例:明天是否下雨,结果不是1就是0。
连续随机变量:即 事件有无数个结果,将这些数字可以用一条光滑的曲线连起来。例如:明天下雨毫米数,可能是1.1、1.11、1.111等数字。
可知:离散随机变量与连续随机变量的概率分布是有差别的。
二、概率分布
数据在统计图中的形状叫做它的分布。
概率分布,将随机变量、概率、分布这三个东西组合起来的一种表现手段。用统计图来表示随机变量的所有可能结果和对应结果发生的概率。 横轴是随机变量的数字,也就是随机事件的所有可能结果,纵轴是横轴上对应结果发生的概率。
根据随机变量类型的不同,概率分布也分为离散概率分布和连续概率分布。
计算离散随机变量的概率公式:概率质量函数(PMF)。本文讨论 4种 常见的离散概率分布:伯努利分布、二项分布、几何分布、泊松分布
计算连续随机变量的概率公式:概率密度函数(PDF)。本文讨论 2种 常见的连续概率分布:正态分布、幂律分布
(一)离散概率分布
1、离散概率分布:伯努利分布
1.1 概念:在同样的条件下,重复地进行相互独立的随机试验。其特点为这个随机试验只有2个可能结果(例如抛硬币试验,要么正面、要么反面)。
1.2 检验是否符合伯努利分布:若某事件符合伯努利试验,则服从伯努利分布,如抛硬币。
1.3 用Python实现伯努利分布
#统计计算包的统计模块
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt
# 第 1 步:定义随机变量为 1 次,抛硬币。正面朝上即为 1,反面朝上即为 0。
# 用 arange() 方法生成等差数列,表示:0为起点,不超过 2,步长为 1。
X = np.arange(0,2,1)
print(X) # [0 1]
# 第 2 步:计算对应分布的概率:概率质量函数(PMF)
# 它返回一个列表,列表中每个元素表示随机变量中对应值的概率
p = 0.5 #硬币朝上的概率
pList = stats.bernoulli.pmf(X,p)
print(pList) # [0.5 0.5]
# 第 3 步:画图
'''
plot默认绘制折线图,本例中只绘制点(下面输入的参数不画线,只画点),
marker:点的形状,值为“o”,表示点为圆圈标记(circle marker)
linestyle:线条的形状,值None表示不显示连接各个点的折线
'''
# 3.1 设置成微软雅黑,支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
# 3.2 创建画布
plt.figure(figsize=(20,8),dpi=80)
# 3.3 绘制图形
plt.plot(X,pList,marker='o',linestyle='None')
'''
vlines用于绘制竖直线(vertical lines),
参数说明:
vlines(x坐标值,y坐标最小值,y坐标最大值)
传入的 X 是一个数组,是给数组中的每个 X坐标 值绘制竖直线,竖直线 y坐标 最小值是0;
y坐标 值最大值是对应pList中的值;
'''
plt.vlines(X,0,pList)
#x轴文本
plt.xlabel('随机变量:抛硬币1次')
#y轴文本
plt.ylabel('概率')
#标题
plt.title('伯努利分布:p=%.1f'% p)
#显示图形
plt.show()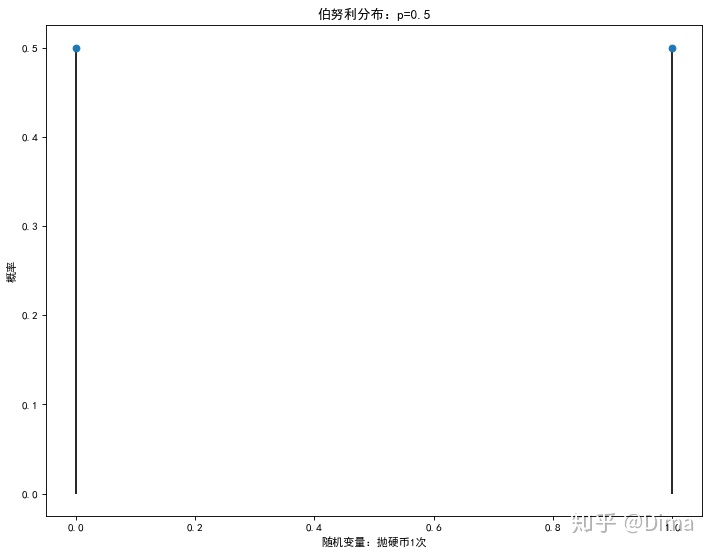
2、离散概率分布:二项分布
2.1 概念:二项分布是求做重复n次独立的伯努利试验中成功k次的概率。
若某件事发生次数固定,我们感兴趣的是成功次数的概率,即可用二项分布计算其概率。例如:抛硬币5次,其中3次正面朝上的概率是多少?
2.2 检验是否符合二项分布
- 做某件事的次数是固定的,次数用 n 表示,n 次某件事是相互独立的;
- 每一次事件都有两个可能的结果(成功,或者失败);
- 每一次成功的概率都相等,成功的概率用 p 表示;
- 想知道成功 k 次的概率是多少?
2.3 如何计算二项分布的概率
例如:抛5次硬币有3次正面朝上的概率,即做了5次伯努利试验,符合二项分布


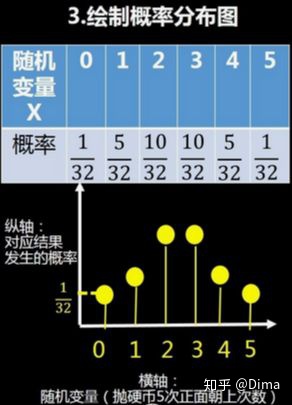
有时候,用逆向思维求概率会更方便,如:求出抛100次硬币有95次正面朝上的概率 = 1 - 5次反面朝上的概率 即可。
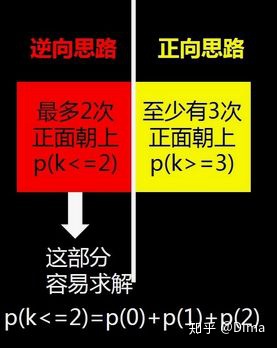
2.4 二项分布的应用:期望与方差

用“期望E”来表示:做某件事,预期能成功多少次 ?
E(k)= n*p=尝试n次 * 每次成功的概率 ,抛5次硬币能正面朝上的次数预期=5 *0.5=2.5次
方差=n*p *(1-p) ,抛5次硬币能正面朝上的次数方差=2.5 * (1-0.5)=1.25
2.5 用 Python 实现二项分布(Binomial Distribution)
# 统计计算包的统计模块
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt
# 第一步,定义随机变量:5次抛硬币,正面朝上的次数
n = 5 # 做某件事情的次数
p = 0.5 # 做某件事情成功的概率(抛一次硬币,正面朝上的概率)
X = np.arange(0,n+1,1)
print(X)
# 第二步,求对应分布的概率,概率质量函数(PMF)
# 它返回一个列表,列表中每个元素表示随机变量中对应值的概率
pList = stats.binom.pmf(X,n,p)
print(pList)
# 第三步,绘图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.figure(figsize=(20,8),dpi=80)
plt.plot(X,pList,marker='o',linestyle='None')
'''
vlines用于绘制竖直线(vertical lines),
参数说明:
vlines(x坐标值,y坐标最小值,y坐标最大值)
传入的 X 是一个数组,是给数组中的每个 X坐标 值绘制竖直线,竖直线 y坐标 最小值是0;
y坐标 值最大值是对应pList中的值;
'''
plt.vlines(X,0,pList)
plt.xlabel('随机变量:抛硬币1次')
plt.ylabel('概率')
plt.title('二项分布:n=%i,p=%.2f' % (n,p))
plt.show()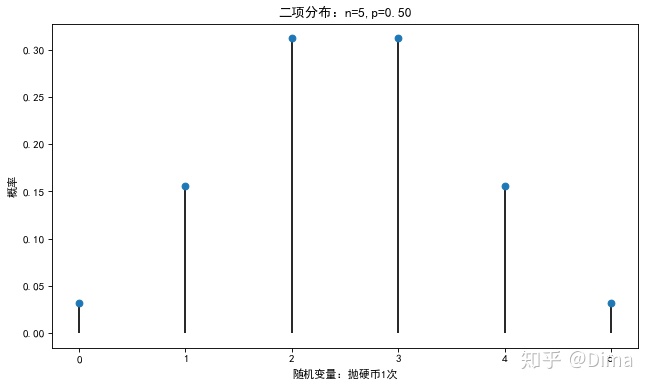
3、离散概率分布:几何分布
3.1 概念:几何分布是求在重复n次伯努利试验中,试验k次才得到第一次成功的概率。想知道尝试某事多次第一次取得成功的概率,可用几何分布计算其概率。
3.2 检验是否符合几何分布
- 做某件事的次数是固定的,次数用 n 表示,n 次某件事是相互独立的;
- 每一次事件都有两个可能的结果(成功,或者失败);
- 每一次成功的概率都相等,成功的概率用 p 表示;
- 想知道第 k 次做某件事情,才取得第1次成功的概率是多少?
3.3 如何计算几何分布的概率
此处,为方便计算,假设一个前提,60%是每个单次表白的成功率。

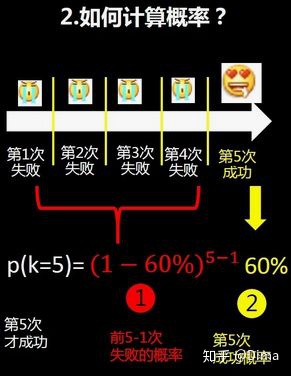

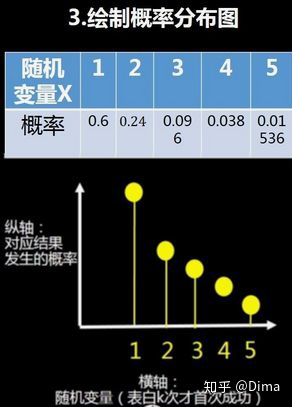
3.4 几何分布的应用:期望与方差
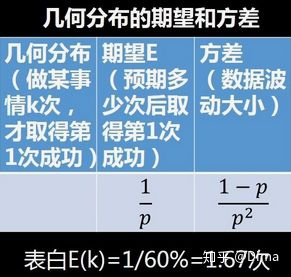
期望E(预期尝试多少次可取得第1次成功) :E(k)=1/p =1/60%=1.67次 (以单次表白成功率为60%计算)--从期望E值可以看出,通过提升自我,让自已变得更强,提高单次成功率p,当p达到100%时,期望E=1。
方差(数据波动大小)=(1-p)/p*p = (1-60%)/(60% * 60%)=1.1111
3.5 用 Python 实现几何分布(Geometric Distribution)
# 统计计算包的统计模块
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt
# 第一步,定义随机变量:首次表白成功的次数,可能是1次,2次,3次。。。(不会是0次)
# 第 k 次做某件事情,才取得第 1 次成功
# 这里我们想知道5次表白成功的概率
k = 5
# 做某件事情成功的概率,这里假设每次表白成功概率都是60%
p = 0.6
X=np.arange(1,k+1,1)
print(X)
# 第二步,求对应分布的概率,概率质量函数(PMF)
# 它返回一个列表,列表中每个元素表示随机变量中对应值的概率
pList=stats.geom.pmf(X,p)
print(pList)
# 第三步,绘图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.figure(figsize=(20,8),dpi=80)
plt.plot(X,pList,marker='o',linestyle='None')
'''
vlines用于绘制竖直线(vertical lines),
参数说明:
vlines(x坐标值,y坐标最小值,y坐标最大值)
传入的 X 是一个数组,是给数组中的每个 X坐标 值绘制竖直线,竖直线 y坐标 最小值是0;
y坐标 值最大值是对应pList中的值;
'''
plt.vlines(X,0,pList)
plt.xlabel('随机变量:表白第k次才首次成功')
plt.ylabel('概率')
plt.title('几何分布:p=%.2f' % p)
plt.show()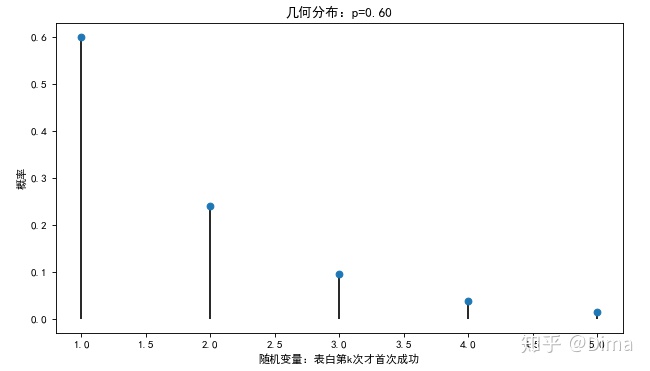
4、离散概率分布:泊松分布
4.1 概念:想知道某个时间范围内发生某件事k次的概率,即用泊松分布计算其概率。例如:一段时间内机器坏的次数
泊松分布的形状会随着平均值的变化而变化。
4.2 检验是否符合泊松分布
- 事件是独立事件
- 在任意相同的时间范围内,事件发生的概率相同
- 你想知道某个时间范围内,发生 k 次的概率是多大
4.3 泊松分布的应用:期望和方差

4.4 用 Python 实现泊松分布(Poisson Distribution)
# 统计计算包的统计模块
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt
# 第一步,定义随机变量:已知某路口发生事故的比率是每天2次,那么在此处一天内发生k次事故的概率是多少?
mu = 2 # 平均值:每天发生2次事故
k = 4 # 次数,现在想知道每天发生4次事故的概率。包含了发生0次、1次、2次、3次、4次事故
X = np.arange(0,k+1,1)
print(X)
# 第二步,求对应分布的概率,概率质量函数(PMF)
# 它返回一个列表,列表中每个元素表示随机变量中对应值的概率
#分别表示发生1次、2次、3次、4次事故的概率
pList = stats.poisson.pmf(X,mu)
print(pList)
# 第三步,绘图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.figure(figsize=(20,8),dpi=80)
plt.plot(X,pList,marker='o',linestyle='None')
'''
vlines用于绘制竖直线(vertical lines),
参数说明:
vlines(x坐标值,y坐标最小值,y坐标最大值)
传入的 X 是一个数组,是给数组中的每个 X坐标 值绘制竖直线,竖直线 y坐标 最小值是0;
y坐标 值最大值是对应pList中的值;
'''
plt.vlines(X,0,pList)
plt.xlabel('随机变量:某路口发生k次事故')
plt.ylabel('概率')
plt.title('泊松分布:平均值mu=%i' % mu)
plt.show()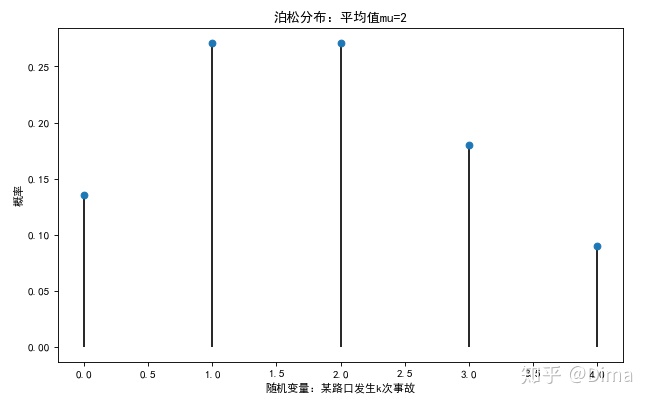
总结一下,每种离散分布,调用不同的方法实现而已。
- 伯努利分布:pList = stats.bernoulli.pmf(X,p)
- 二项分布:pList = stats.binom.pmf(X,n,p)
- 几何分布:pList=stats.geom.pmf(X,p)
- 泊松分布:pList = stats.poisson.pmf(X,mu)
(二)随机概率分布
1、正态分布
1.1 概念:
正态分布(The Normal Distribution),由被称为:拉普拉斯分布、高斯分布
正态分布是连续随机变量,其概率为正态分布曲线下方一定数字范围的面积
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形。
1.2 案例:
- 人的身高、手臂长度、肺活量等都符合正态分布。
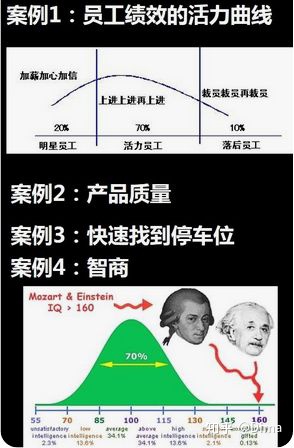
- 正态分布案例1:员工绩效的活力曲线--末位淘汰制
- 正态分布案例2:产品质量--质量管理领域会用6个标准差来排除掉不合格的产品
- 正态分布案例3:快速找到停车位--远离商场大门口的位置,更容易找到车位。
- 正态分布案例4:智商
- 理想的社会财富分配也符合正态分布
- 现实的社会财富分配是符合幂律分布
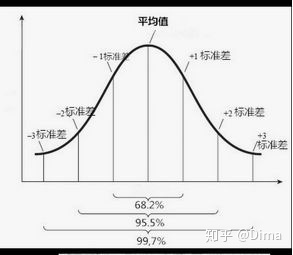
1.3 正态分布的概率计算
正态分布是连续随机变量分布图,它的概率是正态分布曲线下方一定数字范围内的面积。
微信公众号的每篇文章点赞数服从正态分布,现在计算低于1.05的占的概率是多少?即k<1.05的概率=p (k<1.05)
1)第1步:确定概率范围 p (k<1.05)
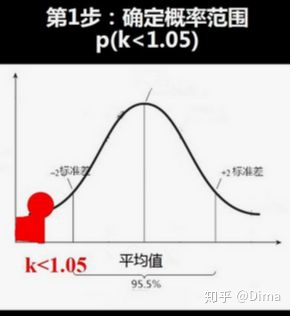
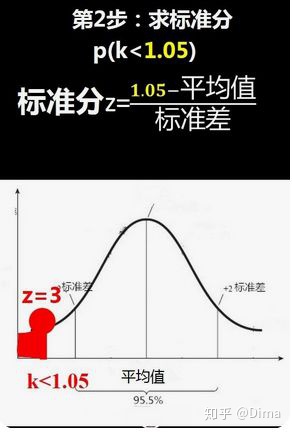
2)第2步:求标准分 z p (k<1.05)
标准分z = ( 1.05-平均值)/ 标准差 ,根据平均值和标准差就可以计算出标准分,这里假设计算出来的标准分是-3,代表1.05这个数值距离平均值3个标准差,因为是负数,所以在平均值的左边。
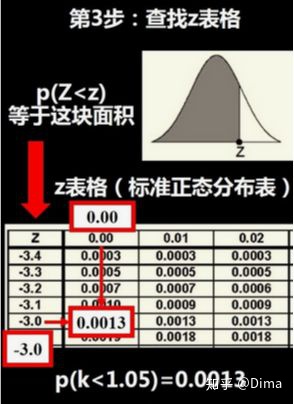
3)查找z表格-标准正态分布表(是标准正态分布中标准分与概率数值对应关系的表)
根据标准正态分布表,在已知标准分z的情况下,可以快速地查找到对应的概率数值。
标准分z,可拆分为:整数和第一个小数位构成的数、第二个小数位的数,在z表格的第一列查找到标准分“整数和第一个小数位构成的数”所在位置,再到z表格第一行查找到标准分“第二个小数位的数”所在位置,在查找到的行位置和列位置的交叉处的数值,即是对应的概率值。
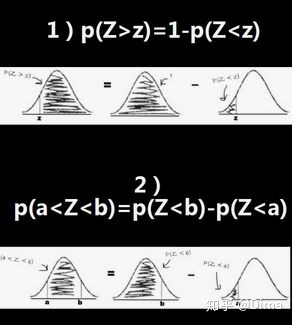
4)推广应用:计算大于标准分的概率 和 计算两个标准分之间的区间概率
计算大于标准分的概率:p(Z>z)=1-p(Z<z)
计算两个标准分之间的区间概率:p(a<Z<b)=p(Z<b)-p(Z<a)
5)正态分布-实际应用
项目:一项轮胎质量保证承诺的服务,如果轮胎的行驶里程没有达到质量保证的行驶里程,公司将以折扣价提供更换轮胎的服务,同时从公司的角度出发,又要考虑这项服务的成本。
条件:公司希望,达到折扣质量保证条件的轮胎数(满足以折扣价更换的轮胎数量)不要超过出售轮胎总数的10%。
问题:出售的轮胎质量保证行驶的里程数应设置在多少呢?
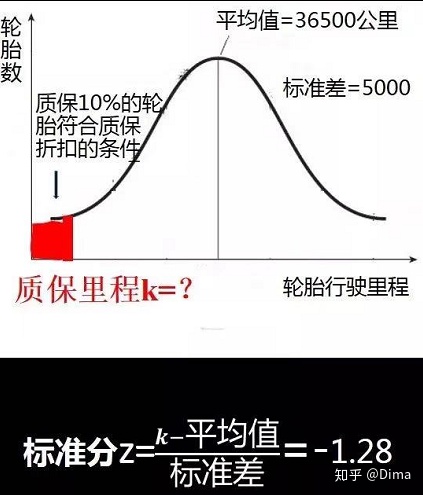
- 从数据库中得到:该款轮胎可行驶里程的相关信息:平均值为36500公里、标准差为5000、数据集成正态分布(绘制:横轴-轮胎行驶里程数、纵轴-对应的轮胎数)
- 从问题中得到:想要在这项目服务中控制住成本,只能允许10%的轮胎满足以折扣价更换的条件,即只允许10%以下概率的轮胎可行驶里程数低于质保,对应到上图正态分布曲线图,是左侧红色的值为10%的面积。
- 查找z表格得到,概率为10%对应的标准分为:-1.28。
- 通过公式:标准分z=(k-平均值)/标准差=-1.28 =(k-36500)/5000=-1.28 ,k= 30100公里。
- 测算结果:若希望满足以折扣价更换的轮胎数量不要超过出售轮胎总数的10%,轮胎的质保里程数应设置在30100公里。
概率分布在提供数据分析决策所需信息方面,起到非常重要的作用。一旦对某一特大应用问题的特点和概率分布有所了解,就可以取得有关问题的概率信息。概率虽然不能直接给出决策建议,但可以帮助决策者更好地了解与问题相关的风险和不确定的信息,最终这些信息可以辅助决策都更好地做出正确的决策。
2、幂律分布
又被称为:长尾理论。语言学家Zipf、经济学家帕累托(Pareto)
常见的幂律分布有:马太效应、二八法则。
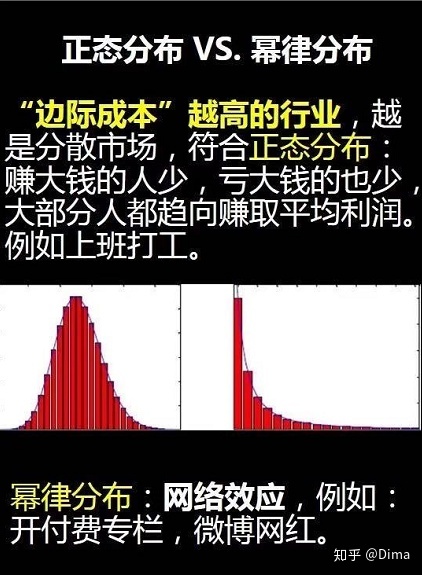
- 网络效应:某产品对一名用户的价值取决于这产品的用户数量,用户数量增加,产品价值就提升,反过来,产品价值就提升,用户数量增加,当用户总数突破一个临界点后,会进入一个赢家通吃的状态,如:腾讯的微信。
- 英文单词的使用数量符合幂律分布
- 互联网上微博的粉丝数量符合幂律分布,少量的大V聚集着大量的粉丝。
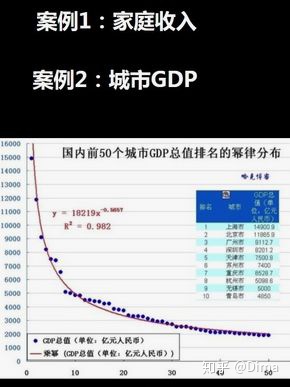
- 国内前50个城市GDP总值排名呈现幂律分布
三、知识点总结