课外扩展-红黑树的删除操作

删除操作：

二叉树的删除操作：

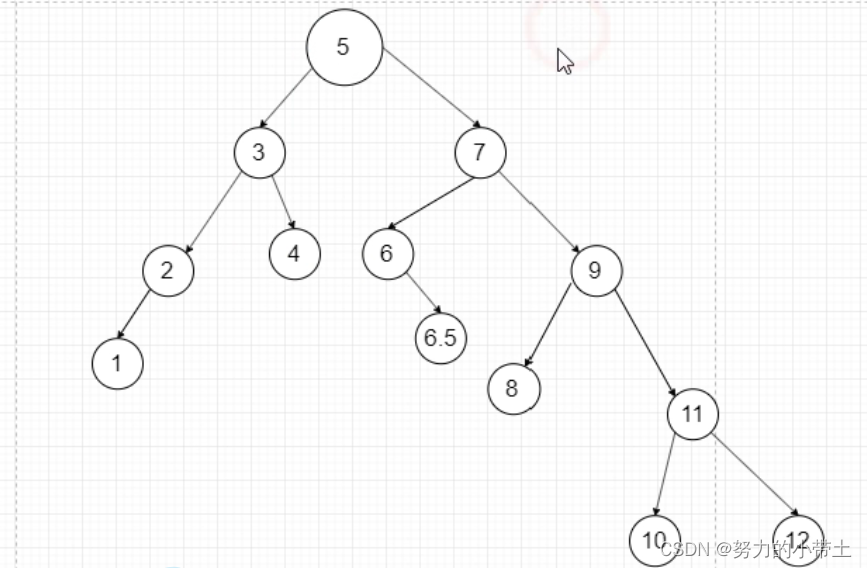
若要删除值’5’节点，我们一般不是直接摘除’5’节点，而是将4或者6的赋值给’5’节点，然后再删除’4’节点或者‘6’节点，也就是将根节点的删除改为删除叶子节点和有一个子节点的节点。直接摘除5会增加许多不必要的指针操作。

复习一下，常规删除操作：

1. 叶子节点直接删除
2. 删除节点有一个子节点，直接使用子节点替代
3. 如果被删除节点有两个子节点，使用前驱或后继节点来替代被删除节点。

被删除的前驱节点和后继节点只有两种情况：

1. 被删除节点是叶子节点。
2. 被删除节点只有一个孩子。

由于被删除节点只有以上两种情况，因此红黑树上的删除节点一定是2-3-4树的叶子节点。故红黑树要删除的节点是叶子节点或叶子节点上面一层，对应2-3-4树就是叶子节点。

在2-3-4树的叶子节点中有2节点3节点和4节点，删除叶子节点时，有两种合法情况，第一种是在3节点中删除一个元素是合法的，第二种是在4节点中删除一或者两个元素是合法的。

基于以上删除操作可知，在算法中找到前驱节点和后继节点至关重要。而红黑树在删除的过程中涉及到许多的调整，具体实现看如下代码：

/*删除操作：
 *1、删除叶子节点直接删除
 *2、被删除的节点有一个子节点，删除它之后使用子节点替代它
 *3、被删除的节点有两个子节点，查找前继或后续节点来替代被删除节点
 */
template <class K,class V>
void RBtree<K, V>::deleteNode(RBtreeNode<K, V>* p)
{
    
    // 有两个子节点的情况，先进行节点替换
    if ( p->left != nullptr && p->right != nullptr)
    {
        // 使用后续节点
        RBtreeNode<K, V>* p_successor = successor(p); 
        // 使用前继节点
        // RBtreeNode<K, V>* p_predecessor = predecessor(p); 
        // 使用前继或者后续的值来替代原节点的值
        p->key = p_successor->key;
        p->value = p_successor->value;
        p = p_successor; //指向要删除节点
    } 
    // 节点替换后，情况3就变成了1和2两种情况，后继节点为便为2-3-4树的叶子节点
    // 删除节点看看有没有左右子树
    RBtreeNode<K, V>* replacement = p->left != nullptr ? p->left : p->right;
    if (replacement != nullptr) // 删除节点有子树
    {
		replacement->parent = p->parent; //先把父亲绑上
		if (p->parent == nullptr) // 说明p是根节点，用replacement来替代根节点
		{
			this->root = replacement;
		}
		else if (p == p->parent->left)
		{
			p->parent->left = replacement;
		}
		else if (p == p->parent->right)
		{
			p->parent->right = replacement;
		}
        // 若被删除颜色为黑色，因为破坏了平衡
        // 所以此时需要调整
		if (p->color == BLACK)
		{
            // 此时改颜色就好了
			fixAfterdelete(replacement);
		}

		p->parent = nullptr;
		p->left = nullptr;
		p->right = nullptr;
        
    }
    else if (replacement == nullptr)//若没有子节点则说明替代节点为叶子节点
    {
		// 因为要保证黑色平衡，所以若删除节点是黑色要先调整
        // 调整过程其实为像兄弟姐妹来借子节点，具体实现仍然是依靠左右旋的算法
		if (p->color == BLACK)
		{
			fixAfterdelete(p);
		}
		//再删除
		//这里多添加根节点的判断是因为经过fixAfterRemove()之后
		//p可能变成根节点
		if (p->parent != nullptr)
		{
			if (p == p->parent->left)
			{
				p->parent->left = nullptr;
			}
			else if (p == p->parent->right)
			{
				p->parent->right = nullptr;
			}
			p->parent = nullptr; // 双向清空
		}
       
    }
    else if (p->parent == nullptr) // 删除节点就是根节点
    {
        this->root = nullptr;
    }
}
template<class K,class V>
void RBtree<K, V>::fixAfterdelete(RBtreeNode<K, V>* p)
{
    while (p != root && colorof(p)==BLACK) // p为根节点的时候直接退出循环
    {
        //先判断p是父节点的左子还是右子
        if (p->parent->left == p) // 若是左子树
        {
            RBtreeNode<K, V>* rnode = p->parent->right; // 取兄弟节点
            if (rnode->color == RED)// 若兄弟为红色，说明该节点是假兄弟节点(其实一定会有兄弟的，所以不需要判断兄弟的有无(因为2-3-4树的性质))
            {
                // 当兄弟节点是红色的时候，其恰好为假兄弟节点
                // 那么就需要做相应的处理，用以查找真正的兄弟节点
                // 此时在2-3-4树中，其父节点为一黑一红的3节点，红色便为p的假兄弟节点
                // 因为是三节点树故必须有三个子节点，当我自身父节点的右子节点为假兄弟节点时
                // 说明其他两个子节点连接在红色的下面，此时只需要左旋即可
                //        x(黑)
                //       /   \ 
                //      p(黑) 假兄弟节点（红）
                //            /      \ 
                //          a(黑)     b(黑)    其中a,b为真兄弟节点
                rnode->parent->color = RED;
                rnode->color = BLACK;
                leftRotate(rnode->parent); //左旋
                // 找到真正的兄弟节点
                rnode = p->parent->right;
            }
            //找兄弟节点借，若兄弟节点没的借
            if (rnode->left->color==BLACK && rnode->right->color== BLACK)
            {
                //没的借，先将兄弟节点本身去红保证子树平衡
                //但对于上面的又不平衡因此需要不断的递归
                //直到遇到一组树中根节点为红节点，
                //那么便停止递归(在while外面将其染成黑色即可)
                rnode->color = RED;
                p = p->parent;
            }
            else //若兄弟节点有的借
            {
                if (rnode->right->color==BLACK)//若右节点空。则左节点一定有东西，此时需要旋转处理
                {
                    //旋转前先变色
                    rnode->left->color = BLACK;
                    rnode->color = RED;
                    //旋转
                    rightRotate(rnode);
                }
                // 三四节点都要经历这种变色和旋转
                rnode->color = rnode->parent->color;
                rnode->parent->color = BLACK;
                rnode->right->color = BLACK;
                // 旋转
                leftRotate(rnode->parent);
                // 有的借之后便可以直接结束循环
                p = root; //将指针赋给根节点结束循环
            }
        }else//若是右子节点
        {
			RBtreeNode<K, V>* lnode = p->parent->left;
			if (lnode->color == RED)// 若兄弟为红色，其实一定会有兄弟的，所以不需要判断兄弟的有无(因为2-3-4树的性质)
			{
                lnode->parent->color = RED;
                lnode->color = BLACK;
				rightRotate(lnode->parent); //左旋
				// 找到真正的兄弟节点
                lnode = p->parent->left;
			}
			//找兄弟节点借，若兄弟节点没的借
			if (lnode->right->color == BLACK && lnode->left->color == BLACK)
			{
				//情况复杂，等下再写
				lnode->color = RED;
				p = p->parent;
			}
			else //若兄弟节点有的借
			{
				if (lnode->left->color == BLACK)//若右节点空。则左节点一定有东西，此时需要旋转处理
				{
					//旋转前先变色
                    lnode->right->color = BLACK;
                    lnode->color = RED;
					//旋转
					leftRotate(lnode);
				}
				// 三四节点都要经历这种变色和旋转
                lnode->color = lnode->parent->color;
                lnode->parent->color = BLACK;
                lnode->left->color = BLACK;
				// 旋转
				rightRotate(lnode->parent);
				// 有的借之后便可以直接结束循环
				p = root; //将指针赋给根节点结束循环
			}
        }
    }
    // 若为红色的情况则直接变黑
    p->color = BLACK;
}