来源：Taotao Tu原创。

前面的帖子，我们介绍了异常值识别与处理的全流程方法。

但是，在有一个细节上，还需要格外注意，即如何精确识别出异常值的范围？

我们来看一个具体的例子

1.导入数据

webuse hsng

2.异常点的初步识别

让我们来初步看看，哪些变量可能存在异常点的问题。

首先，我们来看看变量的基本属性

describe

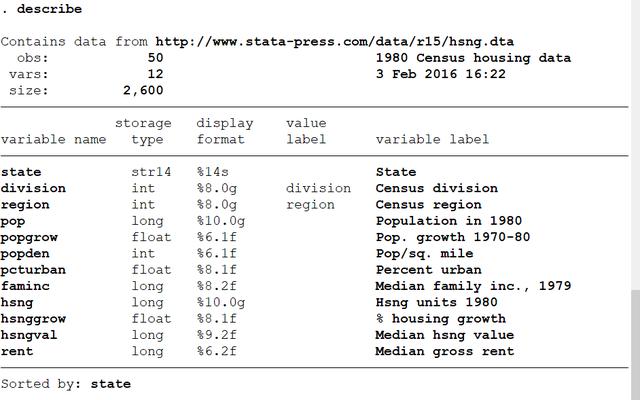
从上图可以看出，除了state是string变量，其他的均为数值型变量。

接下来，让我们初步识别一下 如何甄别 存在异常值的变量

graph box division region pop popgrow popden pcturban faminc hsng hsnggrow hsngval rent

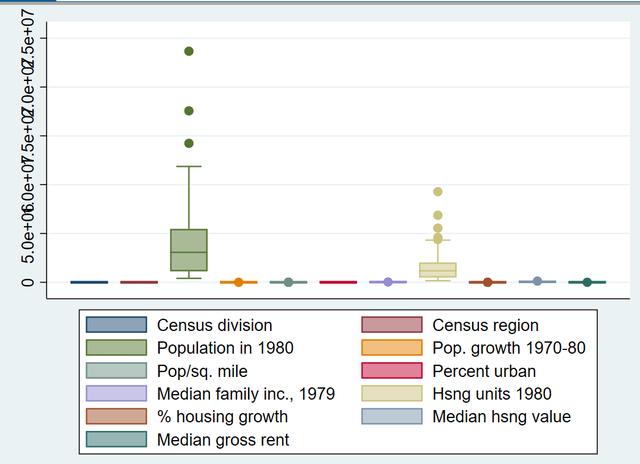
可以看到，存在异常值的序列比较多，最为突出的是pop和hsng。我们来详细分析一下pop序列

3.异常值的精确识别

首先，分析一下pop序列的统计特征

sum pop,detail

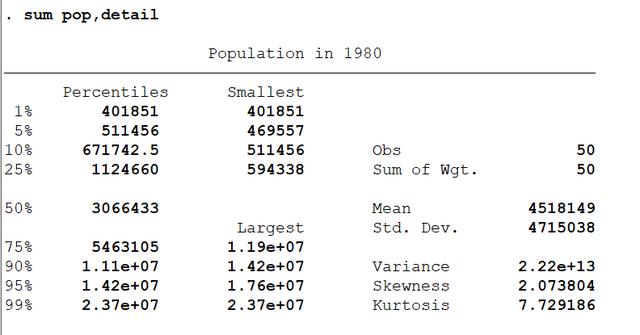
正如 “使用stata软件识别异常值——graph box方法(原创)”
https://www.toutiao.com/i6835121633397572109/ 所提到的

如果有样本落到 最小值(Q1-1.5*IQR)与最大值(Q3+1.5*IQR)区间之外，就可以判定为异常值。

其中，第一个四分位数(Q1)，也叫做25th percentile或者lower quartile； 第二个四分位数(Q2)，也叫做中值或者50th percentile； 第三个四分位数(Q3)，也叫做75th percentile。

因此，计算上述区间的关键是 引用25th percentile，50th percentile,75th percentile。

我们来具体看一个命令

display r(p25), r(p50), r(p75)

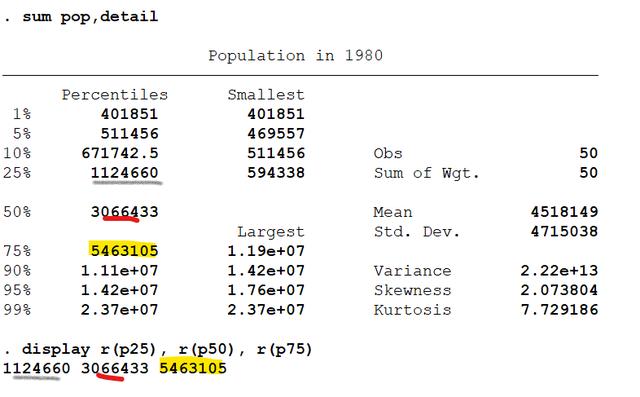
最小值(Q1-1.5*IQR)计算命令如下：

scalar Minimum=r(p25)-1.5*(r(p75)-r(p25))

最大值(Q3+1.5*IQR)计算命令如下：

scalar Maximum=r(p75)+1.5*(r(p75)-r(p25))

想看看结果吗？

display Minimum, Maximum

可以看到，当样本落到【-5383007.5，11970773】之外时，就可断定为异常值。

再绘制一下graph box，更直观地看看异常值的分布

graph box pop

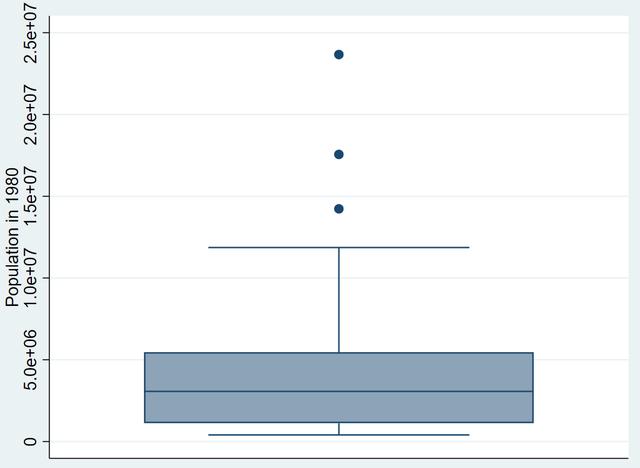
4.异常值的精确缩尾

目前已经找到了判断异常点的合理区间。那么，如果精确缩尾异常点呢？
在这里，我们采取右侧缩尾对数据进行处理

gen pop_win=pop

replace pop_win=Maximum if pop>Maximum
让我们来检验一下，看看得到的 pop_win序列是否已经消除了异常点。
graph box pop pop_win

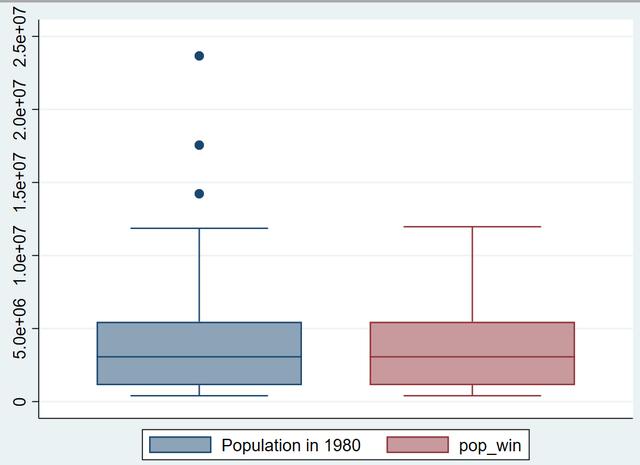
哇~！ 大功告成，是不是很有成就感？别着急，让我们看一看另一个大招。

5.实现pop与hsng序列异常点识别与右侧缩尾的批处理

那么，如何实现上述步骤的自动化批处理呢？来看看我们的代码组合clear

webuse hsng

*pop序列异常值判断区间的计算

sum pop,detail

scalar Minimum=r(p25)-1.5*(r(p75)-r(p25))

scalar Maximum=r(p75)+1.5*(r(p75)-r(p25))

*pop序列异常值的精确右侧缩尾

gen pop_win=pop

replace pop_win=Maximum if pop>Maximum

*hsng序列异常值判断区间的计算

sum hsng,detail

scalar Minimum=r(p25)-1.5*(r(p75)-r(p25))

scalar Maximum=r(p75)+1.5*(r(p75)-r(p25))

*hsng序列异常值的精确右侧缩尾

gen hsng_win=hsng

replace hsng_win=Maximum if hsng>Maximum

graph box pop pop_win hsng hsng_win

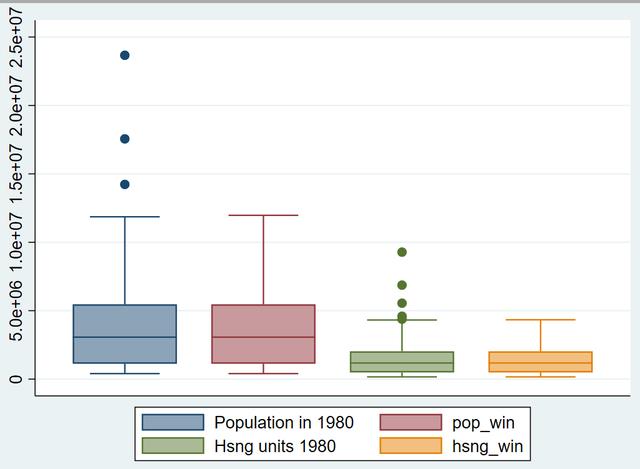
大家可以看到，pop_win和hsng_win序列就是处理好以后的序列(这两个序列的graph box中已经看不到●)。通过上面精炼的代码，我们就可以实现多序列的异常值精准识别与缩尾处理。
上述代码具有很强的通用性。只要将pop或hsng替换成你所需要处理的变量，就可以实现自动批处理了。

思考题：

如果打算采用右侧截尾法来处理异常点，该如何修改代码？