手动编写神经网络前向/反向传递
前向传递
\qquad前向传递的原理非常容易,如下图所示。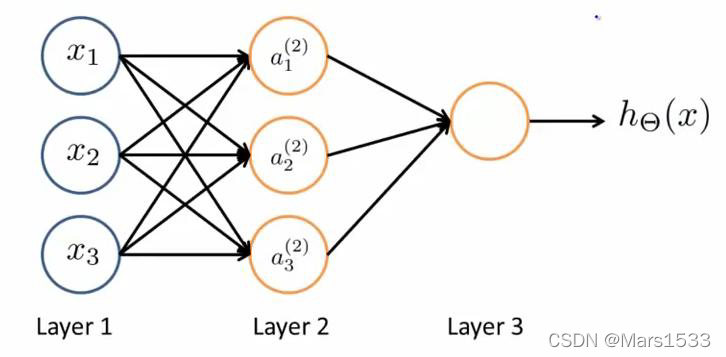
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) h Θ ( x ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) (1) \begin{aligned} &a_{1}^{(2)}=g\left(\Theta_{10}^{(1)} x_{0}+\Theta_{11}^{(1)} x_{1}+\Theta_{12}^{(1)} x_{2}+\Theta_{13}^{(1)} x_{3}\right) \\ &a_{2}^{(2)}=g\left(\Theta_{20}^{(1)} x_{0}+\Theta_{21}^{(1)} x_{1}+\Theta_{22}^{(1)} x_{2}+\Theta_{23}^{(1)} x_{3}\right) \\ &a_{3}^{(2)}=g\left(\Theta_{30}^{(1)} x_{0}+\Theta_{31}^{(1)} x_{1}+\Theta_{32}^{(1)} x_{2}+\Theta_{33}^{(1)} x_{3}\right) \\ &h_{\Theta}(x)=g\left(\Theta_{10}^{(2)} a_{0}^{(2)}+\Theta_{11}^{(2)} a_{1}^{(2)}+\Theta_{12}^{(2)} a_{2}^{(2)}+\Theta_{13}^{(2)} a_{3}^{(2)}\right) \end{aligned} \tag{1}a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)hΘ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))(1)
反向传递
\qquad从最后一层的误差开始计算,误差是激活单元的预测( a k ( 4 ) ) (a_k^{(4)})(ak(4))与实际值( y k ) (y^k)(yk)之间的误差,( k = 1 : K ) (k=1:K)(k=1:K)。
\qquad用δ \deltaδ表示误差,则有:
δ ( 4 ) = a ( 4 ) − y (2) \delta^{(4)}=a^{(4)}-y \tag{2}δ(4)=a(4)−y(2)
\qquad利用这一层的误差去计算前一层的误差,换句话说,计算除最后一层外的误差需要用到后一层的误差。
δ ( 3 ) = ( Θ ( 3 ) ) T δ ( 4 ) ⋅ ∗ g ′ ( z ( 3 ) ) (3) \delta^{(3)}=\left(\Theta^{(3)}\right)^{T} \delta^{(4)} \cdot * g^{\prime}\left(z^{(3)}\right) \tag{3}δ(3)=(Θ(3))Tδ(4)⋅∗g′(z(3))(3)
\qquad其中,g ′ ( z ( 3 ) ) g^{\prime}\left(z^{(3)}\right)g′(z(3))是S i g m o i d SigmoidSigmoid函数的导数,g ′ ( z ( 3 ) ) = a ( 3 ) ⋅ ∗ ( 1 − a ( 3 ) ) g^{\prime}\left(z^{(3)}\right)=a^{(3)} \cdot *\left(1-a^{(3)}\right)g′(z(3))=a(3)⋅∗(1−a(3)),z zz是未经过S函数的节点。( Θ ( 3 ) ) T δ ( 4 ) \left(\Theta^{(3)}\right)^{T} \delta^{(4)}(Θ(3))Tδ(4)是权重导致的误差的和。
\qquad同理得到:
δ ( 2 ) = ( Θ ( 2 ) ) T δ ( 3 ) ∗ g ′ ( z ( 2 ) ) (4) \delta^{(2)}=\left(\Theta^{(2)}\right)^{T} \delta^{(3)} * g^{\prime}\left(z^{(2)}\right) \tag{4}δ(2)=(Θ(2))Tδ(3)∗g′(z(2))(4)
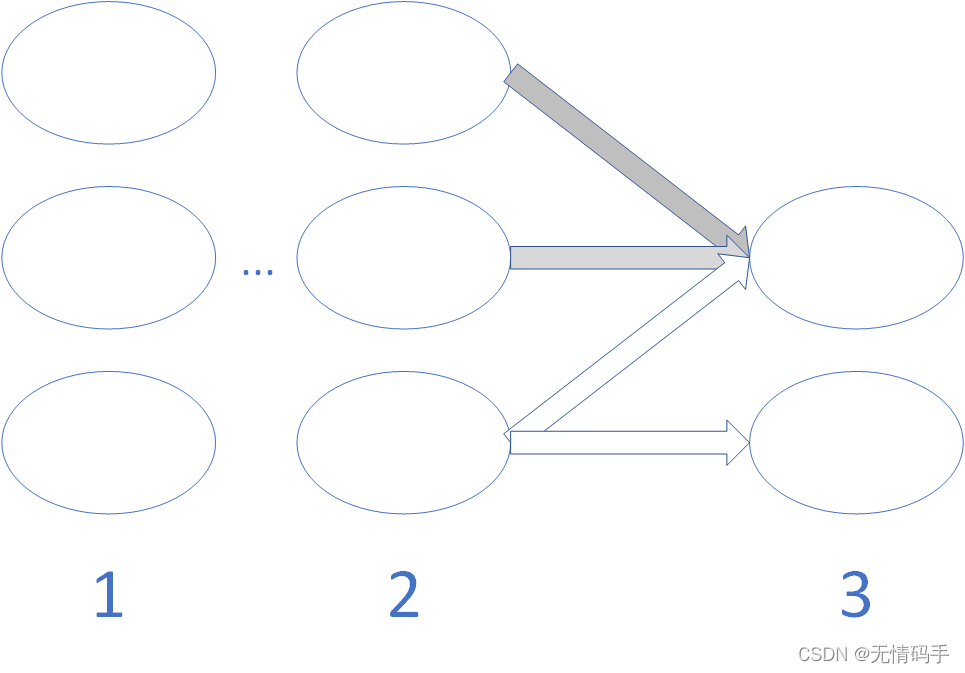
\qquad( Θ ( n ) ) T δ ( n + 1 ) \left(\Theta^{(n)}\right)^{T} \delta^{(n+1)}(Θ(n))Tδ(n+1)的解释如下图所示。由第2层的最后一个节点指出2个箭头,他参与到了第三层的这两个节点中,因此δ 2 ( 2 ) = θ 12 ( 2 ) ∗ δ 1 ( 3 ) + θ 22 ( 2 ) ∗ δ 2 ( 3 ) \delta_2^{(2)}=\theta_{12}^{(2)}*\delta^{(3)}_{1}+\theta_{22}^{(2)}*\delta^{(3)}_{2}δ2(2)=θ12(2)∗δ1(3)+θ22(2)∗δ2(3)。δ ( 2 ) \delta^{(2)}δ(2)可以理解为全部节点的误差,它的长度是3 33。
\qquad假设λ = 0 \lambda=0λ=0,不做任何正则化处理时,有:∂ ∂ Θ i j ( l ) J ( Θ ) = a i j ( l ) δ i l + 1 \frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=a_{i j}^{(l)} \delta_{i}^{l+1}∂Θij(l)∂J(Θ)=aij(l)δil+1,i ii是当前层的第i ii个节点的误差,j是对应到θ \thetaθ的每一个值(上一层a aa的每一个值),δ l + 1 \delta^{l+1}δl+1就是和a l a^lal挂钩的。
\qquad如果我们考虑正则化处理,并且我们的训练集是一个特征矩阵而非向量。在上面的特殊情况中,我们需要计算每一层的误差单元来计算代价函数的偏导数。在更为一般的情况中,我们同样需要计算每一层的误差单元,但是我们需要为整个训练集计算误差单元,此时的误差单元也是一个矩阵。我们用Δ i j ( l ) \Delta_{i j}^{(l)}Δij(l)来表示这个误差矩阵,第l ll层的第i ii个激活单元受到第j jj个参数影响而导致的误差。(举例:如果l ll层10个节点,l − 1 l-1l−1层30个节点,那么这个误差矩阵的维度是( 10 , 30 ) (10,30)(10,30))。
\qquad算法表示为如下,其中,a表示每层激活函数后得到的值,m mm 表示样本数目。
f o r i = 1 : m { s e t a ( i ) = x ( i ) p e r f o r m f o r w a r d p r o p a g a t i o n t o c o m p u t e a ( l ) f o r l = 1 , 2 , 3 … . L U s i n g δ ( L ) = a ( L ) − y i p e r f o r m b a c k p r o p a g a t i o n t o c o m p u t e a l l p r e v i o u s l a y e r e r r o r v e c t o r Δ i j ( l ) : = Δ i j ( l ) + a j ( l ) δ i l + 1 } (5) \begin{aligned} for \quad i=1: m \{\\ &set \quad a^{(i)}=x^{(i)}\\ &perform \,\,\, forward \,\,\, propagation \,\,\, to \,\,\, compute\,\,\, a^{(l)}\,\,\, for \,\,\,l=1,2,3 \ldots . L\\ &Using \,\,\, \delta^{(L)}=a^{(L)}-y^{i}\\ &perform \,\,\,back\,\,\, propagation\,\,\, to\,\,\, compute\,\,\, all\,\,\, previous \,\,\,layer\,\,\, error\,\,\, vector\\ &\Delta_{i j}^{(l)}:=\Delta_{i j}^{(l)}+a_{j}^{(l)} \delta_{i}^{l+1}\\ &\} \end{aligned}\tag{5}fori=1:m{seta(i)=x(i)performforwardpropagationtocomputea(l)forl=1,2,3….LUsingδ(L)=a(L)−yiperformbackpropagationtocomputeallpreviouslayererrorvectorΔij(l):=Δij(l)+aj(l)δil+1}(5)
\qquada j ( l ) δ i l + 1 a_{j}^{(l)} \delta_{i}^{l+1}aj(l)δil+1这里是a j ( l ) a_{j}^{(l)}aj(l)意味着是l ll层的所有节点a与l + 1 l+1l+1层的第i ii个节点相乘->一个矩阵( m , n ) (m,n)(m,n) m mm是l + 1 l+1l+1层节点数,n nn是l ll层节点数。
\qquadδ ( n ) \delta^{(n)}δ(n)是由本层伸出去的θ ( n ) \theta^{(n)}θ(n)算的。Δ i j ( l ) \Delta_{ij}^{(l)}Δij(l)的j jj的数目由节点a ( l ) a^{(l)}a(l)得到,i ii的数目由δ l + 1 \delta^{l+1}δl+1得到。计算方法也是本层( l ) (l)(l)的每个节点和( l + 1 ) (l+1)(l+1)的第i ii误差相乘计算得到。由于a ( l ) a^{(l)}a(l)和δ l + 1 \delta^{l+1}δl+1挂钩,用它俩去算θ \thetaθ的误差Δ \DeltaΔ矩阵。δ ( l + 1 ) T ∗ a l \delta^{(l+1)T} * a^{l}δ(l+1)T∗al (举例:( 1 , 26 ) T ∗ ( 1 , 401 ) − > ( 26 , 401 ) (1,26)^T * (1,401) -> (26,401)(1,26)T∗(1,401)−>(26,401))。
\qquad区别:δ ( n ) \delta^{(n)}δ(n)以本层n nn为中心,看伸出去的去计算,Δ i j ( l ) \Delta_{ij}^{(l)}Δij(l)是以( l + 1 ) (l+1)(l+1)层为中心(l ll层θ \thetaθ就对应l + 1 l+1l+1层)和上层的a aa相乘。
\qquad即首先用正向传播方法计算出每一层的激活单元,利用训练集的结果与神经网络预测的结果求出最后一层的误差,然后利用该误差运用反向传播法计算出直至第二层的所有误差。
\qquad加正则化后的梯度计算:
D i j ( l ) : = 1 m Δ i j ( l ) + λ Θ i j ( l ) if j ≠ 0 D i j ( l ) : = 1 m Δ i j ( l ) if j = 0 (6) \begin{aligned} &D_{i j}^{(l)}:=\frac{1}{m} \Delta_{i j}^{(l)}+\lambda \Theta_{i j}^{(l)} \quad \text { if } \quad j \neq 0\\ &D_{i j}^{(l)}:=\frac{1}{m} \Delta_{i j}^{(l)} \quad \text { if } j=0 \end{aligned} \tag{6}Dij(l):=m1Δij(l)+λΘij(l) if j=0Dij(l):=m1Δij(l) if j=0(6)
代码实例
\qquad接下来,我将用逻辑回归来解决经典的MNIST手写数字识别问题,下面是它详细的代码介绍。
\qquad首先载入数据集:
import numpy as np
from scipy.io import loadmat
data = loadmat('ex4data1.mat')
X = data['X']
y = data['y']
\qquad对y标签进行一次one-hot 编码。
\qquadone-hot 编码将类标签n(k类)转换为长度为k的向量,其中索引n为“hot”(1),而其余为0。
\qquadScikitlearn有一个内置的实用程序,我们可以使用这个。
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder(sparse=False)
y_onehot = encoder.fit_transform(y)
print(y_onehot.shape)
\qquad我们要为此练习构建的神经网络具有与我们的实例数据(400 +偏置单元)大小匹配的输入层,25个单位的隐藏层(带有偏置单元的26个),以及一个输出层(10个单位对应我们的一个one-hot编码类标签)。
\qquad我们首先需要实现的是评估一组给定的网络参数的损失的代价函数:
def sigmoid(z):
return 1 / (1 + np.exp(-z))
#前向传播函数
def forward_propagate(X, theta1, theta2):
# 神经网络整个运算过程是针对于一个样本来说的,输入层长度为400就代表x有400维
m = X.shape[0]
# 给维度为400的x在最前面加一个1,用于偏置
a1 = np.insert(X, 0, values=np.ones(m), axis=1)
# a1 是 1 * 401 所以这一层要有维度为401维的\theta 它的个数决定了隐藏层的单元个数
# 因为\theta是针对下一层来说的 \theta_ji j代表下一层要算的这个单元 i是前一层从1到N的所有单元
# \theta_ji可以理解为它转置了 \theta本身是(x,401)的shape第一维是代表第n个下一层的节点对应的\theta 算的时候是转置了来算的
z2 = a1 * theta1.T
# 得到a2后,也要给他加一维的1,用于偏置
a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)
z3 = a2 * theta2.T
h = sigmoid(z3)
return a1, z2, a2, z3, h
#代价函数
def cost(params, input_size, hidden_size, num_labels, X, y, learning_rate):
m = X.shape[0]
X = np.matrix(X)
y = np.matrix(y)
# reshape the parameter array into parameter matrices for each layer
# 前面是对参数的切片,后面是\theta的矩阵维度(n,size+1) n->隐藏层的个数/最终one-hot的label数
theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
# run the feed-forward pass
a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
# compute the cost
J = 0
# y本身是向量化的,m是总体样本的数目
# 因为这里用的是one-hot编码,h_\theta(x)也是sigmoid函数,其实和之前的逻辑回归是非常相似的
# 只不过是最后把这10维全加起来了(有的地方是0,所以之前是一样的)
for i in range(m):
first_term = np.multiply(-y[i, :], np.log(h[i, :]))
second_term = np.multiply((1 - y[i, :]), np.log(1 - h[i, :]))
J += np.sum(first_term - second_term)
J = J / m
return J
#正则化代价函数
def cost_n(params, input_size, hidden_size, num_labels, X, y, learning_rate):
m = X.shape[0]
X = np.matrix(X)
y = np.matrix(y)
# reshape the parameter array into parameter matrices for each layer
theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
# run the feed-forward pass
a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
# compute the cost
J = 0
for i in range(m):
first_term = np.multiply(-y[i, :], np.log(h[i, :]))
second_term = np.multiply((1 - y[i, :]), np.log(1 - h[i, :]))
J += np.sum(first_term - second_term)
J = J / m
# add the cost regularization term
# theta1[:,1:]第一维的:就是每行的 \theta 每个节点对应的\theta 也就是\theta^l_{ji}的l 外面的整个\Sum np.sum
J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:, 1:], 2)) + np.sum(np.power(theta2[:, 1:], 2)))
return J
\qquad定义反向传播。
\qquad它不仅计算了当前的代价,还返回了参数的梯度。
#梯度计算加正则化的反向传播:
def backprop(params, input_size, hidden_size, num_labels, X, y, learning_rate):
m = X.shape[0]
X = np.matrix(X)
y = np.matrix(y)
# reshape the parameter array into parameter matrices for each layer
theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
# run the feed-forward pass
a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
# initializations
J = 0
delta1 = np.zeros(theta1.shape) # (25, 401)
delta2 = np.zeros(theta2.shape) # (10, 26)
# compute the cost
for i in range(m):
first_term = np.multiply(-y[i, :], np.log(h[i, :]))
second_term = np.multiply((1 - y[i, :]), np.log(1 - h[i, :]))
J += np.sum(first_term - second_term)
J = J / m
# add the cost regularization term
J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:, 1:], 2)) + np.sum(np.power(theta2[:, 1:], 2)))
# perform backpropagation
for t in range(m):
a1t = a1[t, :] # (1, 401)
z2t = z2[t, :] # (1, 25)
a2t = a2[t, :] # (1, 26)
ht = h[t, :] # (1, 10)
yt = y[t, :] # (1, 10)
d3t = ht - yt # (1, 10)
z2t = np.insert(z2t, 0, values=np.ones(1)) # (1, 26)
d2t = np.multiply((theta2.T * d3t.T).T, sigmoid_gradient(z2t)) # (1, 26)
delta1 = delta1 + (d2t[:, 1:]).T * a1t
delta2 = delta2 + d3t.T * a2t
delta1 = delta1 / m
delta2 = delta2 / m
# add the gradient regularization term
delta1[:, 1:] = delta1[:, 1:] + (theta1[:, 1:] * learning_rate) / m
delta2[:, 1:] = delta2[:, 1:] + (theta2[:, 1:] * learning_rate) / m
# unravel the gradient matrices into a single array
grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
return J, grad
\qquad测试梯度下降。输出结果为:6.732102294368071 (10285,)。这里直接计算了m个样本下,随机θ \thetaθ下的代价和梯度。并没有最优化,梯度下降,更新参数的过程。
#反向传播计算的最难的部分(除了理解为什么我们正在做所有这些计算)是获得正确矩阵维度。
J, grad = backprop(params, input_size, hidden_size, num_labels, X, y_onehot, learning_rate)
print(J, grad.shape)
\qquad初始化网络,定义参数。
# 初始化设置
input_size = 400
hidden_size = 25
num_labels = 10
learning_rate = 1
# 随机初始化完整网络参数大小的参数数组
# 这里的params是一维的,后面还要再切片转矩阵
params = (np.random.random(size=hidden_size * (input_size + 1) + num_labels * (hidden_size + 1)) - 0.5) * 0.25
m = X.shape[0]
X = np.matrix(X)
y = np.matrix(y)
print(params.shape)
# 将参数数组解开为每个层的参数矩阵
theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
print(theta1.shape, theta2.shape)
\qquad开始预测。先最小化目标函数得到训练后θ \thetaθ的数值。
#预测:
from scipy.optimize import minimize
# minimize the objective function
fmin = minimize(fun=backprop, x0=params, args=(input_size, hidden_size, num_labels, X, y_onehot, learning_rate),
method='TNC', jac=True, options={'maxiter': 250})
print(fmin)
#得到训练后的\theta值
#开始预测
X = np.matrix(X)
theta1 = np.matrix(np.reshape(fmin.x[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(fmin.x[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
\qquad输入数据得出预测的y值,并计算准确率。
a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
y_pred = np.array(np.argmax(h, axis=1) + 1)
correct = [1 if a == b else 0 for (a, b) in zip(y_pred, y)]
accuracy = (sum(map(int, correct)) / float(len(correct)))
print ('accuracy = {0}%'.format(accuracy * 100))
\qquad最终计算得出,达到的准确率为:accuracy = 99.44%。