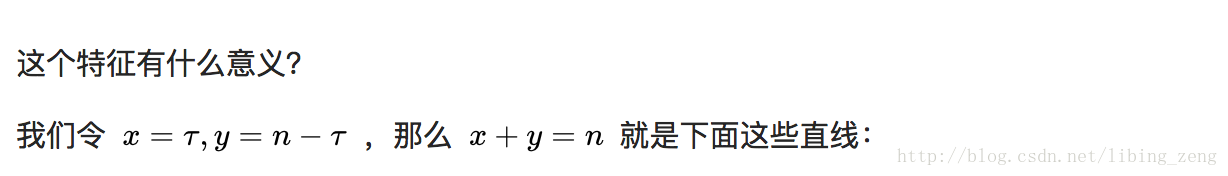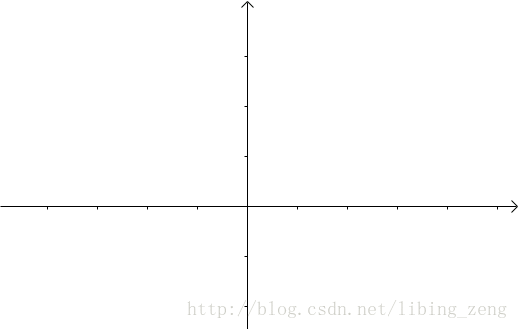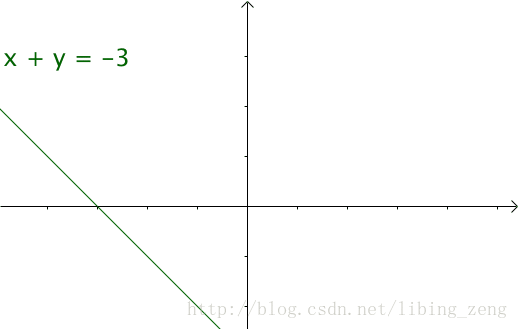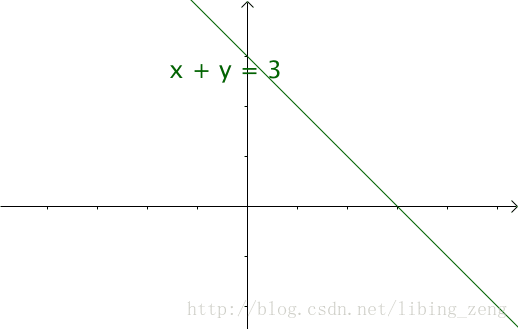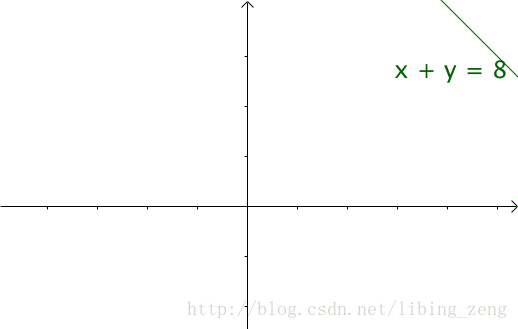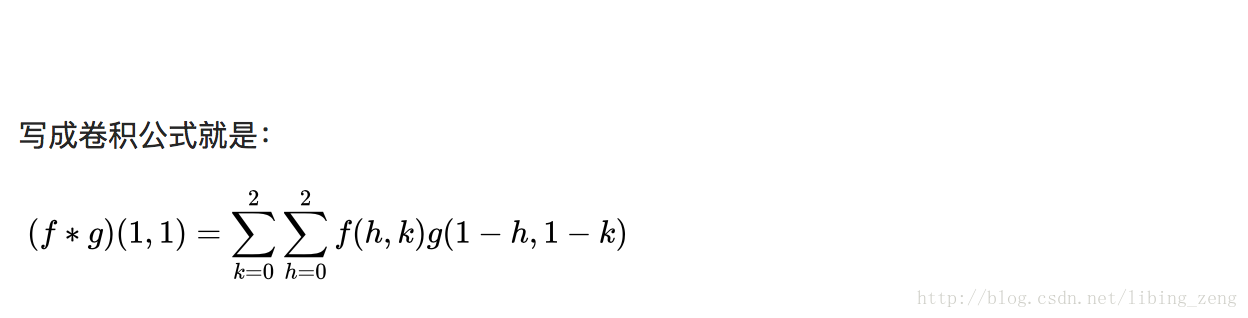文章大部分转自：https://www.zhihu.com/question/22298352?rf=21686447
相应版权归原作者！

笔者的理解：“卷积”就是“加权求和”

“信号与响应的卷积”体现的是：时间上的“加权求和”；
“图像平滑处理的卷积”体现的是：空间上的“加权求和”。

（后文内容为转载）

一、卷积为什么叫“卷”积

从数学上讲，卷积就是一种运算。

某种运算，能被定义出来，至少有以下特征：

首先是抽象的、符号化的
其次，在生活、科研中，有着广泛的作用

比如加法：

a+b ，是抽象的，本身只是一个数学符号
在现实中，有非常多的意义，比如增加、合成、旋转等等

卷积，是我们学习高等数学之后，新接触的一种运算，因为涉及到积分、级数，所以看起来觉得很复杂。

卷积的定义

如果遍历这些直线，就好比，把毛巾沿着角卷起来：

二、卷积应用实例

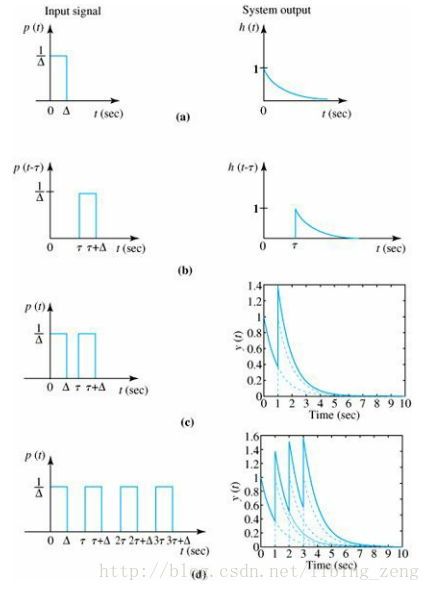
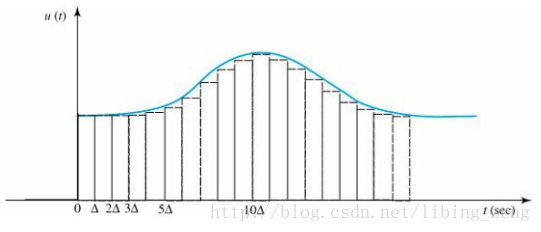
2.1 “信号与系统”相关。（时间上的加权求和）

先看下图，左边是输入信号，右边是输出信号：

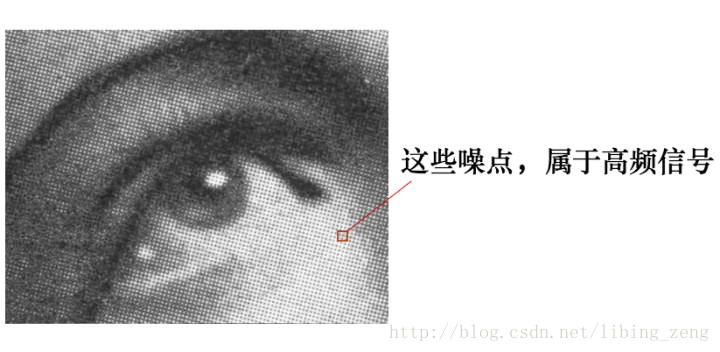
2.2 “图像平滑处理”相关。（空间上的加权求和）

有这么一副图像，可以看到，图像上有很多噪点：

高频信号，就好像平地耸立的山峰：

看起来很显眼。

平滑这座山峰的办法之一就是，把山峰刨掉一些土，填到山峰周围去。用数学的话来说，就是把山峰周围的高度平均一下。

平滑后得到：

卷积可以帮助实现这个平滑算法。

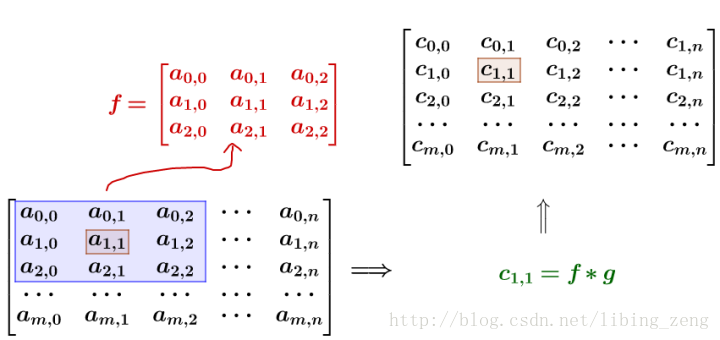
有噪点的原图，可以把它转为一个矩阵：

要注意一点，为了运用卷积， g 虽然和 f 同维度，但下标有点不一样：

用一个动图来说明下计算过程：