算法与数据结构——栈

栈：仅在表尾进行插入和删除操作的线性表
特点为：后入先出 Last In First Out

进栈与出栈

数学性质

当多个编号元素依某种顺序入栈，且可以任意时刻出栈时，可获得编号元素排列的数目恰好满足Catalan函数的计算（n为元素个数）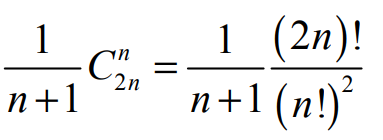

例如：

其进栈次序为：a1,a2,a3
出栈顺序按公式计算n=3，共5种
分别为：a1 a2 a3 ; a3 a2 a1 ; a2 a1 a3 ; a1 a3 a2 ; a2 a3 a1 .
顺序存储
完整代码如下：
前情“predef.h”文件（用于函数返回值的文件）

#ifndef _PREDEF_H
#define _PREDEF_H
//函数结果状态代码
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;//Status是函数返回值类型（函数结果状态码）
#endif//_PREDEF_H

“stack.h”文件（用于实现栈的基本操作）
首先是栈的顺序存储表示（在你使用栈前要先定义一个栈类型）

#pragma once
#include"predef.h"
//-------Stack's sequential stored expression-----
//----storage space initial distribution
#define STACK_INIT_SIZE 100
//----storage space distributive increament
#define STACKINCREAMENT 10
typedef int SElemType;
typedef struct
{
	SElemType *base;//before construct Stack or after clear Stack: base=NULL
	SElemType *top;//top pointer
	int stacksize;//distributed storage space. Unit is element
}SqStack;

sum up:
1.两个int型指针分指头、底
2.一个栈空间

栈的基本操作（示例）
InitStack(&S)// 构造空栈
GetTop(&S, &e)// 获取栈顶元素
Push(&S, e) // 进栈
Pop(&S , &e)// 出栈

InitStack(&S)// 构造空栈 ：

Status InitStack(SqStack &S)// construct empty stack
{
	S.base = new SElemType[STACK_INIT_SIZE];//dynamically distribute storage space
	S.top = S.base;//before construct stack, top pointer point base
	S.stacksize = STACK_INIT_SIZE;
	return OK;
}

GetTop(&S, &e)// 获取栈顶元素 ：

Status GetTop(SqStack &S, SElemType &e)// acquire top's elemnt
{//if stack is not empty, e will return top's elemnt; else return ERORR
	if (S.base == S.top)//if base and top's pointers are the same, stack is empty
	{
		return ERROR;
	}
	e = *(S.top - 1);//top's pior element is valid. In other word, element which top point is invalid
	return OK;
}

sum up:
1.top指针指向的space无效
2.头尾指针相等不能判断满但能判断空

Push(&S, e) // 进栈：

Status Push(SqStack &S, SElemType &e)// push e and make it become top's element
{//if stack is full, add storage space 
	if (S.top-S.base >=S.stacksize)
	{
		SElemType *newbase= new SElemType[S.stacksize+ STACKINCREAMENT];
		for (int i = 0; i < S.stacksize; ++i)//copy primary elements to new stack
		{
			newbase[i] = S.base[i];
		}
		delete[](S.base);//free old storage space
		S.base = newbase;//renew old base pointer
		S.top = S.base + S.stacksize;//renew old top pointer
		S.stacksize += STACKINCREAMENT;//increase storage 
	}
	*S.top++ = e;//first assignment e to S.top, then S.top point next space
	return OK;
}

这里*S.top++=e是 *S.top=e; *S.top++;的顺序。
Pop(&S , &e)// 出栈：

Status Pop(SqStack &S, SElemType &e)
{//if stack is not empty, delete top's element,e will return top's elemnt; else return ERORR
	if (S.base == S.top)//if base and top's pointers are the same, stack is empty
	{
		return ERROR;
	}
	e = *--S.top;//top's next element assignment e, and top point next space
	return OK;
}

这里e=*–S.top是 *S.top–; *S.top=e;的顺序，也就是说栈顶指针指哪 哪就是栈顶而指向的结点被删。
再次创建Sqstack_try.cpp文件用于测试stack

#include"stack.h"
#include<iostream>
#include<stdlib.h>
using namespace std;
typedef int ElemType;
void inputSqstack_int(SqStack &S)
{//input data and store them in Stack
	ElemType temp;//temp is temporary variable store element you input
	int n;//n store the number of the elements
	cout << "你将要像此栈中输入的数据元素个数为:" << '\t';
	cin >> n;
	cout << "依次输入" << n << "个整型数存入顺序栈中" << endl;
	for (int i = 1; i <= n; i++)
	{
		cout << "第" << i << "个整型数进栈中" << '\t';
		cin >> temp;
		Push(S, temp);
	}
	cout << "将输入的" << n << "个整型数依次进栈" << endl;
}
void outputSqstack(SqStack &S)
{//output the stack's elements
	cout << "将栈的元素从栈顶到栈尾依次出栈" << endl;
	ElemType temp = 0;//temp is temporary variable store element you want to output
	for (int i = *(S.top-1); i >= *(S.base); i--)
	{
		Pop(S, temp);
		cout << temp << '\t';
	}
	cout << endl;
}
int main()
{
	SqStack numstack;
	InitStack(numstack);
	inputSqstack_int(numstack);
	int num;
	GetTop(numstack,num);
	cout << "栈顶元素为" << num << endl;
	outputSqstack(numstack);
	system ("pause");
	return 0;
}