CSDN话题挑战赛第2期
参赛话题:算法题解
LeetCode Cookbook 树(5)
本节内容主要为几道很有趣的 “应用题”。
863. 二叉树中所有距离为 K 的结点?(model-IX 哈希)
题目链接:863. 二叉树中所有距离为 K 的结点
题目大意:给定一个二叉树(具有根结点 root), 一个目标结点 target ,和一个整数值 k 。
返回到目标结点 target 距离为 k 的所有结点的值的列表。 答案可以以 任何顺序 返回。
例如: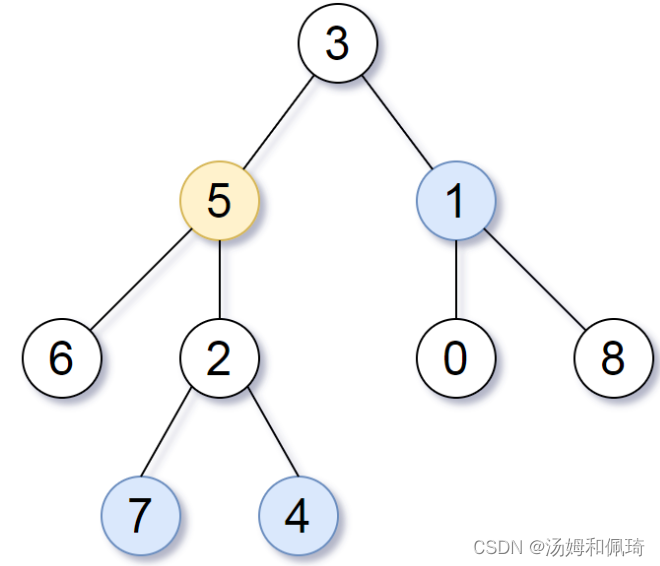
输入:root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
输出:[7,4,1]
解释:所求结点为与目标结点(值为 5)距离为 2 的结点,值分别为 7,4,以及 1
- 解题思路:遗留问题 不太明白!
- 时间复杂度:O ( N ) O(N)O(N) N为二叉树的结点数
- 空间复杂度:O ( N ) O(N)O(N)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:
# 父节点 哈希表
parM = {root.val:None}
def findPar(node: TreeNode) -> None:
if node.left:
parM[node.left.val] = node
findPar(node.left)
if node.right:
parM[node.right.val] = node
findPar(node.right)
def findAns(root: TreeNode,nodeFrom: TreeNode,depth: int,k: int) -> None:
if root is None: return
if depth == k:
self.ans.append(root.val)
return
if root.left != nodeFrom:
findAns(root.left,root,depth+1,k)
if root.right != nodeFrom:
findAns(root.right,root,depth+1,k)
if parM[root.val] != nodeFrom:
findAns(parM[root.val],root,depth+1,k)
self.ans = list()
findPar(root)
findAns(target,None,0,k)
return self.ans
979. 在二叉树中分配硬币(model-IX 脑筋急转)
题目链接:979. 在二叉树中分配硬币
题目大意:给定一个有 N 个结点的二叉树的根结点 root,树中的每个结点上都对应有 node.val 枚硬币,并且总共有 N 枚硬币。
在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点,或者从子结点移动到父结点。)。
返回使每个结点上只有一枚硬币所需的移动次数。
例如: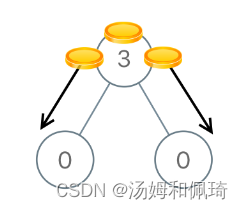
输入:[3,0,0]
输出:2
解释:从树的根结点开始,我们将一枚硬币移到它的左子结点上,一枚硬币移到它的右子结点上。
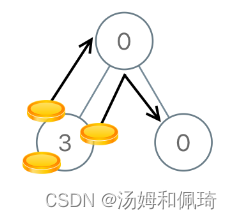
输入:[0,3,0]
输出:3
解释:从根结点的左子结点开始,我们将两枚硬币移到根结点上 [移动两次]。
然后,我们把一枚硬币从根结点移到右子结点上。
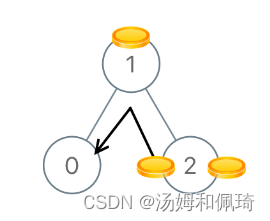
输入:[1,0,2]
输出:2
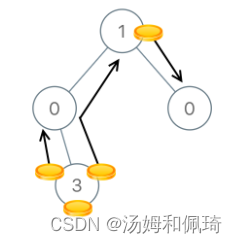
输入:[1,0,0,null,3]
输出:4
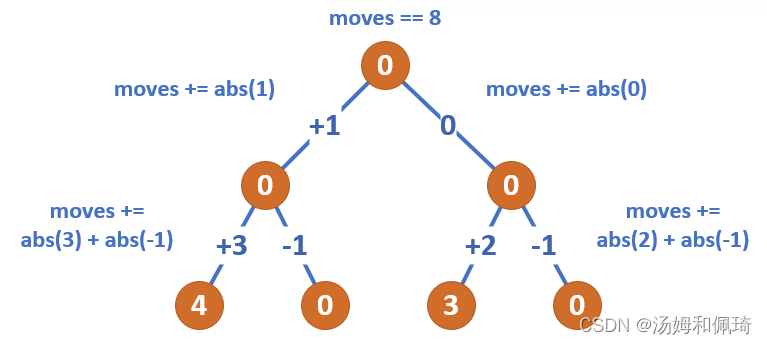
- 解题思路: 本题 读懂后就已经成功一大半了,这道题需要转换思想的考虑,硬币移动问题是否可以转化为 纯数学运算,建议查看 这篇题解 中的图示 非常详尽地展示,上图转自对应题解链接。
- 时间复杂度:O ( N ) O(N)O(N) N为二叉树的结点数
- 空间复杂度:O ( H ) O(H)O(H) H为树的高度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def distributeCoins(self, root: Optional[TreeNode]) -> int:
# 找规律题 很让人心酸哎!
self.ans = 0
def dfs(node: Optional[TreeNode]) -> int:
if node is None: return 0
L,R = dfs(node.left),dfs(node.right)
self.ans += abs(L)+abs(R)
return node.val+L+R-1
dfs(root)
return self.ans
1110. 删点成林(model-IX 集合)
题目链接:1110. 删点成林
题目大意:如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。
返回森林中的每棵树。你可以按任意顺序组织答案。
例如: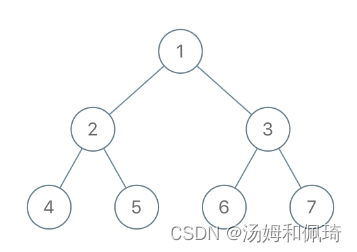
输入:root = [1,2,3,4,5,6,7], to_delete = [3,5]
输出:[[1,2,null,4],[6],[7]]
输入:root = [1,2,4,null,3], to_delete = [3]
输出:[[1,2,4]]
- 解题思路:遗留问题 不太明白!
- 时间复杂度:O ( N ) O(N)O(N) N为二叉树的结点数
- 空间复杂度:O ( I ) O(I)O(I) I为 集合to_delete 所含元素个数
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def delNodes(self, root: TreeNode, to_delete: List[int]) -> List[TreeNode]:
self.ans = []
self.to_delete = to_delete
self.delete(root)
if root.val not in to_delete: self.ans.append(root)
return self.ans
def delete(self,node:TreeNode) -> bool:
if node is None: return False
L = self.delete(node.left)
R = self.delete(node.right)
if L: node.left = None
if R: node.right = None
if node.val in self.to_delete:
if node.left: self.ans.append(node.left)
if node.right: self.ans.append(node.right)
return True
return False
1145. 二叉树着色游戏(model-IX 集合)
题目链接:1110. 删点成林
题目大意:有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中,给出二叉树的根节点 root,树上总共有 n 个节点,且 n 为奇数,其中每个节点上的值从 1 到 n 各不相同。
游戏从「一号」玩家开始(「一号」玩家为红色,「二号」玩家为蓝色),最开始时,
「一号」玩家从 [1, n] 中取一个值 x(1 <= x <= n);
「二号」玩家也从 [1, n] 中取一个值 y(1 <= y <= n)且 y != x。
「一号」玩家给值为 x 的节点染上红色,而「二号」玩家给值为 y 的节点染上蓝色。
之后两位玩家轮流进行操作,每一回合,玩家选择一个他之前涂好颜色的节点,
将所选节点一个 未着色 的邻节点(即左右子节点、或父节点)进行染色。
如果当前玩家无法找到这样的节点来染色时,他的回合就会被跳过。
若两个玩家都没有可以染色的节点时,游戏结束。着色节点最多的那位玩家获得胜利 ✌️。
现在,假设你是「二号」玩家,根据所给出的输入,假如存在一个 y 值可以确保你赢得这场游戏,则返回 true;若无法获胜,就请返回 false。
例如: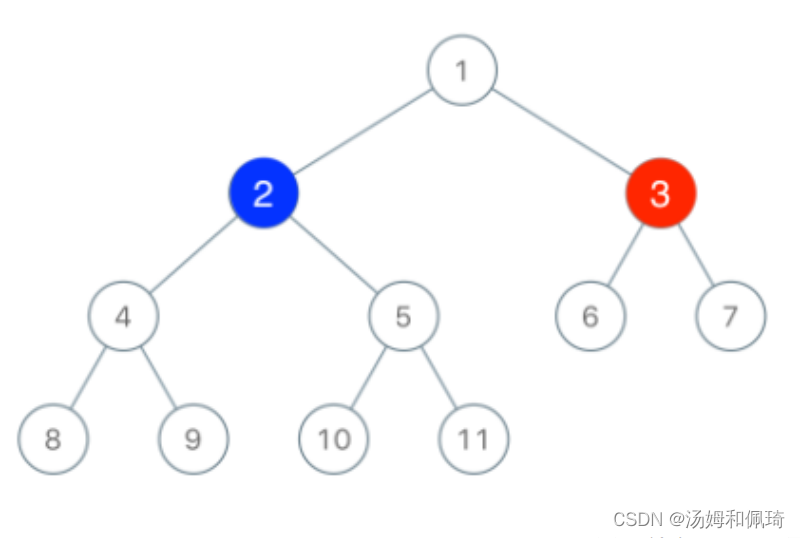
输入:root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
输出:True
解释:第二个玩家可以选择值为 2 的节点。
- 解题思路:非常令人头疼的应用题 题目长的要命 其实就是一个 计数题目! 哈哈,具体看代码。
- 时间复杂度:O ( N ) O(N)O(N) N为二叉树的结点数
- 空间复杂度:O ( N ) O(N)O(N)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def count(self,node: Optional[TreeNode]) -> int:
return 1+self.count(node.left)+self.count(node.right) if node else 0
def find(self,node: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if node is None: return
if node.val == val: return node
return self.find(node.left,val) or self.find(node.right,val)
def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:
node = self.find(root,x)
return n>2*self.count(node) or \
n<2*self.count(node.left) or n<2*self.count(node.right)
968. 监控二叉树(model-IX 状态转移)
题目链接:968. 监控二叉树
题目大意:给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
例如:
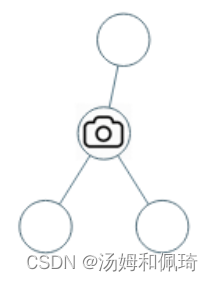
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
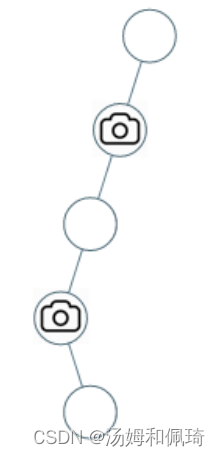
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
- 解题思路:指定三个三个状态:
- 状态0表示左右子树没有全被监控,我需要搞一台,res += 1,返回状态2;
- 状态1表示左右子树已经被监控,但我没被监控到,需要装相机,返回状态0;
- 状态2表示我被监控了,但我的上头没有被监控,返回状态1.
- 时间复杂度:O ( N ) O(N)O(N) N为二叉树的结点数
- 空间复杂度:O ( N ) O(N)O(N)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def minCameraCover(self, root: TreeNode) -> int:
self.res = 0
def lrd(node):
if node is None:
return 1 #空节点不需要被人拍也不用拍别人,直接返回被拍了就好
left = lrd(node.left)
right = lrd(node.right)
if left == 0 or right == 0:
# 左右子树没被监控 需要相机 那我就搞一个 并返回状态2
self.res += 1
return 2
if left == 2 or right == 2:
#左右子树有一个相机 我被辐射到里面了 返回1
return 1
else:# left == 1 and right == 1:
# 左右子树 都被拍过了 那么我就需要自己搞一个 故返回 需要拍摄的状态 0
return 0
if lrd(root) == 0:
##看看根节点是不是需要被拍
self.res += 1
return self.res
834. 树中距离之和?(model-IX 树形规划 图)
题目链接:834. 树中距离之和
题目大意:给定一个无向、连通的树。树中有 n 个标记为 0…n-1 的节点以及 n-1 条边 。
给定整数 n 和数组 edges , edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。
返回长度为 n 的数组 answer ,其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。
例如: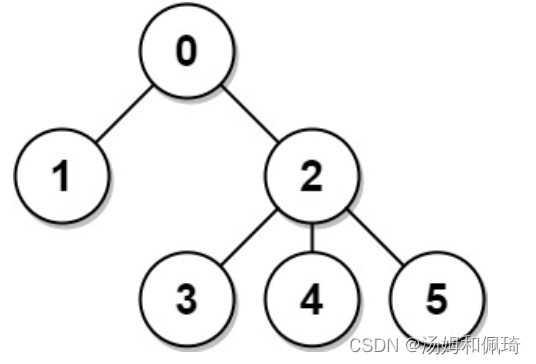
输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此,answer[0] = 8,以此类推。

输入: n = 1, edges = []
输出: [0]
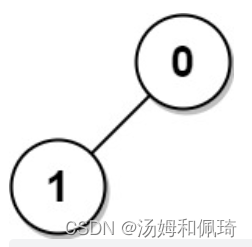
输入: n = 2, edges = [[1,0]]
输出: [1,1]
- 解题思路:树形动态规划 遗留问题!
- 时间复杂度:O ( N ) O(N)O(N) N为树的结点数
- 空间复杂度:O ( N ) O(N)O(N)
class Solution:
def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:
nNums = [0]*n
dis = [0]*n
seen = {0}
dic = [set() for _ in range(n)]
for i,j in edges:
dic[i].add(j)
dic[j].add(i)
def postOrder(i):
num,d = 1,0
for j in dic[i]:
if j not in seen:
seen.add(j)
num1,d1 = postOrder(j)
num += num1
d += d1+num1
nNums[i] = num
return num,d
dis[0] = postOrder(0)[1]
seen = {0}
def dfs(i):
for j in dic[i]:
if j not in seen:
seen.add(j)
dis[j] = dis[i] + (n-2*nNums[j])
dfs(j)
dfs(0)
return dis
总结
努力 奋斗! 这几道趣味题目,挺有趣!主要是要把题目给都明白了,弄清楚应该使用那种数据结构来处理中间变量,这部分题目要考虑的东西比较多,继续学习。