3.22 题解报告
1001 sort
题目
Problem Description
给你n个整数,请按从大到小的顺序输出其中前m大的数。
Input
每组测试数据有两行,第一行有两个数n,m(0<n,m<1000000),第二行包含n个各不相同,且都处于区间[-500000,500000]的整数。
Output
对每组测试数据按从大到小的顺序输出前m大的数。
Sample Input
5 3
3 -35 92 213 -644
Sample Output
213 92 3
题解
就是正常sort啊!
代码
#include<stdio.h>
#include<stdlib.h>
#define N 1000001
int a[N],m;
void Qsort(int low,int high){
int k,i;
k=a[low];
int left=low;
int right=high;
if(left>right)
return ;
while(left!=right){
while(a[right]<k&&left<right)
right--;
if(left<right){
a[left]=a[right];
left++;
}
while(a[left]>k&&left<right)
left++;
if(left<right){
a[right]=a[left];
right--;
}
}
a[left]=k;
if(m<=left+1)Qsort(low,left-1);
else {
Qsort(low,left-1);
Qsort(left+1,high);
}
}
int main(){
int i,j,n;
while(scanf("%d%d",&n,&m)!=EOF){
for(i=0;i<n;i++)scanf("%d",&a[i]);
Qsort(0,n-1);
for(i=0;i<m;i++){
printf("%d",a[i]);
if(i!=m-1)
printf(" ");
}
printf("\n");
}
return 0;
}
1002 EXCEL排序
题目
Problem Description
Excel可以对一组纪录按任意指定列排序。现请你编写程序实现类似功能。
Input
测试输入包含若干测试用例。每个测试用例的第1行包含两个整数 N (<=100000) 和 C,其中 N 是纪录的条数,C 是指定排序的列号。以下有 N
行,每行包含一条学生纪录。每条学生纪录由学号(6位数字,同组测试中没有重复的学号)、姓名(不超过8位且不包含空格的字符串)、成绩(闭区间[0, 100]内的整数)组成,每个项目间用1个空格隔开。当读到 N=0 时,全部输入结束,相应的结果不要输出。
Output
对每个测试用例,首先输出1行“Case i:”,其中 i 是测试用例的编号(从1开始)。随后在 N 行中输出按要求排序后的结果,即:当 C=1 时,按学号递增排序;当 C=2时,按姓名的非递减字典序排序;当 C=3
时,按成绩的非递减排序。当若干学生具有相同姓名或者相同成绩时,则按他们的学号递增排序。
Sample Input
3 1
000007 James 85
000010 Amy 90
000001 Zoe 60
4 2
000007 James 85
000010 Amy 90
000001 Zoe 60
000002 James 98
4 3
000007 James 85
000010 Amy 90
000001 Zoe 60
000002 James 90
0 0
Sample Output
Case 1:
000001 Zoe 60
000007 James 85
000010 Amy 90
Case 2:
000010 Amy 90
000002 James 98
000007 James 85
000001 Zoe 60
Case 3:
000001 Zoe 60
000007 James 85
000002 James 90
000010 Amy 90
题解
https://blog.csdn.net/u014174811/article/details/42087077?utm_source=blogxgwz3
题意非常明确,就是排序,但在这个基础上,对关键值相等的对象按对象另一种键值做相应排序。使用STL中sort()函数可以省大量的编码时间,但运行时间相当大,这里还用到了string类的一系列运算符重载函数(<,>,=),这也使得运行时间消耗增大。
按关键值c的方法:
bool cmp(S a,S b)//用struct S的两个变量做形参{
if(a.c<b.c) return true;//按关键字c非降序排序
return false;
}
sort(arr,arr+N,cmp);//使用sort范型排序
代码
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
struct Stu
{
string num;
string name;
int score;
} stu[100000];
bool cmpNum(Stu a,Stu b){
return a.num<b.num;
}
bool cmpName(Stu a,Stu b){
if(a.name<b.name) return true;
else if(a.name==b.name) return(cmpNum(a,b));
return false;
}
bool cmpScore(Stu a,Stu b){
if(a.score<b.score) return true;
else if(a.score==b.score) return(cmpNum(a,b));
return false;
}
int main()
{
int n,c,i,cnt;
cnt=1;
while(cin>>n>>c&&n)
{
for(i=0; i<n; i++)
cin>>stu[i].num>>stu[i].name>>stu[i].score;
if(c==1)sort(stu,stu+n,cmpNum);
else if(c==2)sort(stu,stu+n,cmpName);
else sort(stu,stu+n,cmpScore);
cout<<"Case "<<cnt++<<":"<<endl;
for(i=0; i<n; i++)
cout<<stu[i].num<<" "<<stu[i].name<<" "<<stu[i].score<<endl;
}
}
1003 Design T-Shirt
题目
Problem Description
Soon after he decided to design a T-shirt for our Algorithm Board on Free-City BBS, XKA found that he was trapped by all kinds of suggestions from everyone on the board. It is indeed a mission-impossible to have everybody perfectly satisfied. So he took a poll to collect people’s opinions. Here are what he obtained: N people voted for M design elements (such as the ACM-ICPC logo, big names in computer science, well-known graphs, etc.). Everyone assigned each element a number of satisfaction. However, XKA can only put K (<=M) elements into his design. He needs you to pick for him the K elements such that the total number of satisfaction is maximized.
Input
The input consists of multiple test cases. For each case, the first line contains three positive integers N, M and K where N is the number of people, M is the number of design elements, and K is the number of elements XKA will put into his design. Then N lines follow, each contains M numbers. The j-th number in the i-th line represents the i-th person’s satisfaction on the j-th element.
Output
For each test case, print in one line the indices of the K elements you would suggest XKA to take into consideration so that the total number of satisfaction is maximized. If there are more than one solutions, you must output the one with minimal indices. The indices start from 1 and must be printed in non-increasing order. There must be exactly one space between two adjacent indices, and no extra space at the end of the line.
Sample Input
3 6 4
2 2.5 5 1 3 4
5 1 3.5 2 2 2
1 1 1 1 1 10
3 3 2
1 2 3
2 3 1
3 1 2
Sample Output
6 5 3 1
2 1
题解
题意:
有n个人对m件衣服评价,求最高的k件衣服的编号,并且把编号从大到小输出,若评价相等,输出编号较小的。
思路:
用结构体保存每件衣服的总评价,并记录编号,根据评价按升序排衣服编号,取前k个编号倒叙输出(很巧妙的解决了输出编号小的问题)。
代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int maxn = 100+10;
double mp[maxn];
int ans[maxn];
int n, m, k;
struct node{
double val=0;
int num;
}p[maxn];
int cmp(const node a, const node b){
return a.val>b.val;
}
int cmp2(const int a, const int b){
return a>b;
}
int main()
{
while( ~scanf("%d%d%d",&n,&m,&k))
{
memset(mp,0,sizeof(mp));
memset(ans,0,sizeof(ans));
for( int i=0; i<m; i++ )
p[i].val = 0;
for( int i=0; i<n; i++ )
{
for(int j=0; j<m; j++ )
{
double u;
scanf("%lf",&u);
p[j].val += u; // 把每件衣服评价相加求总和;
p[j].num = j+1; // 保存衣服编号;
}
}
sort(p,p+m,cmp); //按评价降序排序;
//for(int i=0; i<m; i++ )
// cout << p[i].num <<" ";
//cout<< endl;
for( int i=0; i<k; i++ )
ans[i] = p[i].num; // 保存评价降序前k个编号;
sort(ans,ans+m,cmp2); // 排序编号输出;
int i;
for( i=0; i<k-1; i++ )
printf("%d ",ans[i]);
printf("%d\n",ans[i]);
}
return 0;
}
1004 稳定排序
题目
Problem Description
大家都知道,快速排序是不稳定的排序方法。
如果对于数组中出现的任意a[i],aj,其中a[i]==a[j],在进行排序以后a[i]一定出现在a[j]之前,则认为该排序是稳定的。
某高校招生办得到一份成绩列表,上面记录了考生名字和考生成绩。并且对其使用了某排序算法按成绩进行递减排序。现在请你判断一下该排序算法是否正确,如果正确的话,则判断该排序算法是否为稳定的。
Input
本题目包含多组输入,请处理到文件结束。
对于每组数据,第一行有一个正整数N(0<N<300),代表成绩列表中的考生数目。
接下来有N行,每一行有一个字符串代表考生名字(长度不超过50,仅包含’a’~‘z’),和一个整数代表考生分数(小于500)。其中名字和成绩用一个空格隔开。
再接下来又有N行,是上述列表经过某排序算法以后生成的一个序列。格式同上。
Output
对于每组数据,如果算法是正确并且稳定的,就在一行里面输出"Right"。如果算法是正确的但不是稳定的,就在一行里面输出"Not Stable",并且在下面输出正确稳定排序的列表,格式同输入。如果该算法是错误的,就在一行里面输出"Error",并且在下面输出正确稳定排序的列表,格式同输入。
注意,本题目不考虑该排序算法是错误的,但结果是正确的这样的意外情况。
Sample Input
3
aa 10
bb 10
cc 20
cc 20
bb 10
aa 10
3
aa 10
bb 10
cc 20
cc 20
aa 10
bb 10
3
aa 10
bb 10
cc 20
aa 10
bb 10
cc 20
Sample Output
Not Stable
cc 20
aa 10
bb 10
Right
Error
cc 20
aa 10
bb 10
题解
如果对于数组中出现的任意a[i],aj,其中a[i]==a[j],在进行排序以后a[i]一定出现在a[j]之前,则认为该排序是稳定的。记录一下进入顺序就好了
代码
#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
struct node{
char a[50];
int b;
int c;
}A[305],B[305];
int cmp(node x,node y){
if(x.b == y.b)
return x.c<y.c;
else
return x.b > y.b;
}
int main(){
int n;
while(scanf("%d",&n)==1){
for(int i=0;i<n;i++){
scanf("%s %d",&A[i].a,&A[i].b);
A[i].c = i;
}
sort(A,A+n,cmp);
// for(int i=0;i<n;i++)
// printf("%s %d\n",A[i].a,A[i].b);
for(int i=0;i<n;i++)
scanf("%s %d",&B[i].a,&B[i].b);
int flag=0;
for(int i=0;i<n;i++)
if(A[i].b!=B[i].b){
flag+=1;
break;} //sort is right or no
for(int i=0;i<n;i++)
if(strcmp(A[i].a,B[i].a)!=0){
flag+=2;
break;} //sort is stable or no
if(flag==0)
printf("Right\n");
else if(flag==1 || flag==3){
printf("Error\n");
for(int i=0;i<n;i++)
printf("%s %d\n",A[i].a,A[i].b);
}
else if(flag==2){
printf("Not Stable\n");
for(int i=0;i<n;i++)
printf("%s %d\n",A[i].a,A[i].b);
}
}
return 0;
}
1005 FatMouse’ Trade
题目
Problem Description
FatMouse prepared M pounds of cat food, ready to trade with the cats guarding the warehouse containing his favorite food, JavaBean.
The warehouse has N rooms. The i-th room contains J[i] pounds of JavaBeans and requires F[i] pounds of cat food. FatMouse does not have to trade for all the JavaBeans in the room, instead, he may get J[i]* a% pounds of JavaBeans if he pays F[i]* a% pounds of cat food. Here a is a real number. Now he is assigning this homework to you: tell him the maximum amount of JavaBeans he can obtain.
Input
The input consists of multiple test cases. Each test case begins with a line containing two non-negative integers M and N. Then N lines follow, each contains two non-negative integers J[i] and F[i] respectively. The last test case is followed by two -1’s. All integers are not greater than 1000.
Output
For each test case, print in a single line a real number accurate up to 3 decimal places, which is the maximum amount of JavaBeans that FatMouse can obtain.
Sample Input
5 3
7 2
4 3
5 2
20 3
25 18
24 15
15 10
-1 -1
Sample Output
13.333
31.500
题解
题意
老鼠用猫食物换取自己最喜爱的食物javaBean的过程,当然换取的最终结果是保证最后的JavaBean是最多的,而且是当自己手中的猫食物小于每个仓库所需交换的猫食物时候,可以手中有多少就交换多少。
思路
按照每个仓库javaBean最大的比率排序才能保证最后的交换的javaBean是最大的
代码
#include <iostream>
#include<algorithm>
#include<iomanip>
using namespace std;
//定义输入仓库的结构体
struct trade
{
int javaBean;//代表J
int cat_food;//代表F
double rate;//J和F的比率
};
/*
调用sort排序函数,,因为最后结果要求获得最大的javaBean,所以 按照J与F比值大小排序
比值相等则按照JavaBean大小排序
*/
bool bigger(trade a,trade b)
{
if(a.rate==b.rate)return a.javaBean>b.javaBean;
else return a.rate>b.rate;
}
int main(void)
{
int M,N,temp;
double total_javaBean=0.0;//最后的javaBean总数
trade *input_trade;
while(cin>>M>>N)
{
//M,N都为-1结束
if(M==-1&&N==-1)break;
input_trade=new trade[N];
//输入仓库情况
for(int i=0;i<N;i++)
{
cin>>input_trade[i].javaBean>>input_trade[i].cat_food;
input_trade[i].rate=(double)input_trade[i].javaBean/input_trade[i].cat_food;
}
//对各个仓库按照单位javaBean大小排序
sort(input_trade,input_trade+N,bigger);
temp=M;
for(int j=0;j<N;j++)
{ //剩下的猫食物比仓库所需的猫食物多时,JavaBean总数就直接相加,剩下的猫食物相应减少
if(temp>=input_trade[j].cat_food)
{
total_javaBean+=input_trade[j].javaBean;
temp-=input_trade[j].cat_food;
}else
{
//当剩下猫食物小于仓库所需的,那么就按照比例去取,然后直接跳出循环
total_javaBean+=((double)temp/input_trade[j].cat_food)*input_trade[j].javaBean;
break;
}
}
//格式输出
cout <<setiosflags(ios::fixed)<<setprecision(3)<<total_javaBean<< endl;
total_javaBean=0;
delete input_trade;
}
return 0;
}
1006 Tian Ji – The Horse Racing
题目
Problem Description
Here is a famous story in Chinese history.
“That was about 2300 years ago. General Tian Ji was a high official in the country Qi. He likes to play horse racing with the king and others.”
“Both of Tian and the king have three horses in different classes, namely, regular, plus, and super. The rule is to have three rounds in a match; each of the horses must be used in one round. The winner of a single round takes two hundred silver dollars from the loser.”
“Being the most powerful man in the country, the king has so nice horses that in each class his horse is better than Tian’s. As a result, each time the king takes six hundred silver dollars from Tian.”
“Tian Ji was not happy about that, until he met Sun Bin, one of the most famous generals in Chinese history. Using a little trick due to Sun, Tian Ji brought home two hundred silver dollars and such a grace in the next match.”
“It was a rather simple trick. Using his regular class horse race against the super class from the king, they will certainly lose that round. But then his plus beat the king’s regular, and his super beat the king’s plus. What a simple trick. And how do you think of Tian Ji, the high ranked official in China?”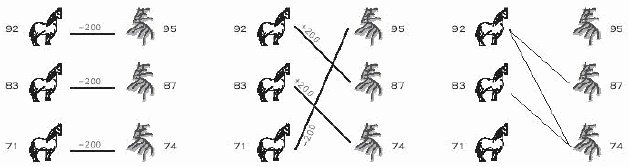
Were Tian Ji lives in nowadays, he will certainly laugh at himself. Even more, were he sitting in the ACM contest right now, he may discover that the horse racing problem can be simply viewed as finding the maximum matching in a bipartite graph. Draw Tian’s horses on one side, and the king’s horses on the other. Whenever one of Tian’s horses can beat one from the king, we draw an edge between them, meaning we wish to establish this pair. Then, the problem of winning as many rounds as possible is just to find the maximum matching in this graph. If there are ties, the problem becomes more complicated, he needs to assign weights 0, 1, or -1 to all the possible edges, and find a maximum weighted perfect matching…
However, the horse racing problem is a very special case of bipartite matching. The graph is decided by the speed of the horses — a vertex of higher speed always beat a vertex of lower speed. In this case, the weighted bipartite matching algorithm is a too advanced tool to deal with the problem.
In this problem, you are asked to write a program to solve this special case of matching problem.
Input
The input consists of up to 50 test cases. Each case starts with a positive integer n (n <= 1000) on the first line, which is the number of horses on each side. The next n integers on the second line are the speeds of Tian’s horses. Then the next n integers on the third line are the speeds of the king’s horses. The input ends with a line that has a single 0 after the last test case.
Output
For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.
Sample Input
3
92 83 71
95 87 74
2
20 20
20 20
2
20 19
22 18
0
Sample Output
200
0
0
题解
题意:
田忌赛马,谁输一局谁就给赢的人200块钱,问田忌最多能赢多少钱。
思路:
1、田忌的一等马>王的一等马,就让田忌的一等马和王的一等马比,因为让其他的马去比肯定会输就要赔钱。
2、田忌的一等马<王的一等马,就让田忌的末等马和王的一等马比(反正其他的马肯定都比王的一等马慢,就用最慢的马把王的一等马耗掉尽量减少损失)。
3、田忌的一等马=王的一等马,就用末等马来比,这就要分两种情况来讨论第一种,田忌的末等马>王的末等马,直接让两者来比正好把末等马耗掉,减少接下来比较的损失。第二种,田忌的末等马<=王的末等马,说明田忌的末等马跑的最慢就让其和王的末等马比,进而减少损失。
代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
bool cmp1(int a,int b){
return a<b;
}
int tian[10010],king[10010];
int main(){
int n;
while(scanf("%d",&n)&&n){
memset(tian,0,sizeof(tian));
memset(king,0,sizeof(king));
int i;
for(i=0;i<n;i++) scanf("%d",&tian[i]);
for(i=0;i<n;i++) scanf("%d",&king[i]);
sort(tian,tian+n,cmp1);
sort(king,king+n,cmp1);
int ans=0;
int max1=n-1,max2=n-1,min1=0,min2=0,cnt=0;
while((cnt++)<n){
if(tian[max1]>king[max2]){
ans=ans+200;
max1--;
max2--;
}
else if(tian[max1]<king[max2]){
ans=ans-200
max2--;
min1++;
}
else{
if(tian[min1]>king[min2]){
ans=ans+200;
min1++;
min2++;
}
else{
if(tian[min1]<king[max2]){
ans=ans-200;
min1++;
max2--;
}
}
}
}
printf("%d\n",ans);
}
return 0;
}
1007 Moving Tables
题目
Problem Description
he famous ACM (Advanced Computer Maker) Company has rented a floor of a building whose shape is in the following figure.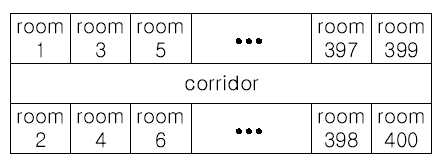
The floor has 200 rooms each on the north side and south side along the corridor. Recently the Company made a plan to reform its system. The reform includes moving a lot of tables between rooms. Because the corridor is narrow and all the tables are big, only one table can pass through the corridor. Some plan is needed to make the moving efficient. The manager figured out the following plan: Moving a table from a room to another room can be done within 10 minutes. When moving a table from room i to room j, the part of the corridor between the front of room i and the front of room j is used. So, during each 10 minutes, several moving between two rooms not sharing the same part of the corridor will be done simultaneously. To make it clear the manager illustrated the possible cases and impossible cases of simultaneous moving.
 For each room, at most one table will be either moved in or moved out. Now, the manager seeks out a method to minimize the time to move all the tables. Your job is to write a program to solve the manager’s problem.
For each room, at most one table will be either moved in or moved out. Now, the manager seeks out a method to minimize the time to move all the tables. Your job is to write a program to solve the manager’s problem.
Input
The input consists of T test cases. The number of test cases ) (T is given in the first line of the input. Each test case begins with a line containing an integer N , 1<=N<=200 , that represents the number of tables to move. Each of the following N lines contains two positive integers s and t, representing that a table is to move from room number s to room number t (each room number appears at most once in the N lines). From the N+3-rd line, the remaining test cases are listed in the same manner as above.
Output
The output should contain the minimum time in minutes to complete the moving, one per line.
Sample Input
3
4
10 20
30 40
50 60
70 80
2
1 3
2 200
3
10 100
20 80
30 50
Sample Output
10
20
30
题解
题意:
南北各200间房间,中间有一走廊。现要将若干特定房间的椅子搬到指定房间,一条走廊只能允许一把椅子过去,已知每个椅子从任意房间到任意房间的时间都是10分钟,求经过最优分配后所需的最短时间。
输入:第一行测试个数,第二行要搬几(n)把椅子,后面分别输入椅子的起始房间和终点房间号(n组每组一行)。
输出:一共所需最短时间。
分析:
1号房间和2号房间都对应位置1的走廊,3号房间和4号房间对应位置2的走廊,一共有200个这样的位置。我用a[201]定义这些位置,其中某位置的值就是经历这个位置的次数。如果从某一号房到另一号房,所经历的每个位置的次数都+1,最后再全体扫描下哪个位置经历次数最多,输出值便是这个位置的值*10。不要遗忘可能起始房间号比终止房间号大
代码
#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
int vis[202];
struct Node{
int x;
int y;
}node[203];
int main(){
int t;
scanf("%d",&t);
while(t--){
int n;
scanf("%d",&n);
memset(vis,0,sizeof(vis));
int a,b;
for(int i=0;i<n;i++)
{
scanf("%d%d",&a,&b);
if(a>b){
int temp=b;
b=a;
a=temp;
}
if(a&1)
a+=1;
if(b&1)
b+=1;
node[i].x=a/2;
node[i].y=b/2;
}
for(int j=0;j<n;j++)
{
for(int i=node[j].x;i<=node[j].y;i++)
vis[i]++;
}
int max=-1;
for(int i=0;i<201;i++)
if(vis[i]>max)
max=vis[i];
printf("%d\n",max*10);
}
}
1008 今年暑假不AC
题目
Problem Description
“今年暑假不AC?”
“是的。”
“那你干什么呢?”
“看世界杯呀,笨蛋!”
“@#$%^&*%…”
Input
输入数据包含多个测试实例,每个测试实例的第一行只有一个整数n(n<=100),表示你喜欢看的节目的总数,然后是n行数据,每行包括两个数据Ti_s,Ti_e (1<=i<=n),分别表示第i个节目的开始和结束时间,为了简化问题,每个时间都用一个正整数表示。n=0表示输入结束,不做处理。
Output
对于每个测试实例,输出能完整看到的电视节目的个数,每个测试实例的输出占一行。
Sample Input
12
1 3
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
5 10
4 14
2 9
0
Sample Output
5
题解
因为一个节目对应一个开始时间和一个结束时间,所以,将这两个时间放到一个结构体中,然后对结束时间按照从小到大的顺序进行排序,如果结束的时间相同的话,就将开始的时间按照从大到小的顺序排序,然后开始比较,如果开始的时间比前一个结束的时间迟,就k++,最终k的值即为所求
代码
#include <stdio.h>
#include <algorithm>
using namespace std;
struct node {
int t1;//电视开始时间
int t2;//电视的结束时间
}a[105];
int cmp(node u,node v)//对节目按照结束时间从小到大排序,如果结束的时间相同,则按照开始时间从大到小的排序!
{
if(u.t2==v.t2)//为什么要将开始的时间从大到小排序呢?是因为如果结束时间相同的话,开始的
return u.t1>v.t1;//越迟,看节目的时间越短,你就能尽可能的多看电视!
return u.t2<v.t2;//例如:2-3,3-4,2-4,你肯定会看2-3,3-4的两个电视,而不看2-4这个电视
}
int main()
{
int n,i,j,k,t;
while(scanf("%d",&n)&&n){
for(i=0;i<n;i++)//有n个开始和结束时间,将时间输入
scanf("%d%d",&a[i].t1,&a[i].t2);
sort(a,a+n,cmp);//对时间进行排序
for(i=1,t=a[0].t2,k=1;i<n;i++){//如果开始 的时间比他这个结束的时间迟,则就k++
if(a[i].t1>=t){//说明这个电视你能够看
t=a[i].t2;
k++;
}
}
printf("%d\n",k);//k代表能看的电视的个数
}
return 0;
}
1009 Max Sum
题目
Problem Description
Given a sequence a[1],a[2],a[3]…a[n], your job is to calculate the max sum of a sub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 + (-1) + 5 + 4 = 14.
Input
The first line of the input contains an integer T(1<=T<=20) which means the number of test cases. Then T lines follow, each line starts with a number N(1<=N<=100000), then N integers followed(all the integers are between -1000 and 1000).
Output
For each test case, you should output two lines. The first line is “Case #:”, # means the number of the test case. The second line contains three integers, the Max Sum in the sequence, the start position of the sub-sequence, the end position of the sub-sequence. If there are more than one result, output the first one. Output a blank line between two cases.
Sample Input
2
5 6 -1 5 4 -7
7 0 6 -1 1 -6 7 -5
Sample Output
Case 1:
14 1 4
Case 2:
7 1 6
题解
一、暴力求解方法
遍历所有的连续子序列,取和最大的那个.唯一决定一个连续子序列的指标为序列起始、结束索引,分别设置为i和j则,要求a[i],…,a[j]的和.其中0<=i<n, i<=j<n,如此遍历即可.i和j为两层循环,求和一层循环,共三层循环,复杂度O(n^3)
二、预处理
先求出从a[0]开始到a[i]的和S_i(0<=i<n),一次循环. 再计算S_i+1,j = S_j - S_i, 注意下表的范围.由于不用求和,只需要计算两个值的差值,所以只有i和j循环,两层,复杂度O(n^2)
三、分治法
把序列分成两块计算,用递归分别求出两块序列中的最大子序列和,然后从序列中间向两边遍历求出包含中心的序列的最大和。返回最大的那个序列和。
四、累积求和的方法
遍历序列的时候对Sum进行累计,如果Sum累积后小于0的话就把Sum重置为负无穷,每次更新Sum的最大值。最后便能求出最大值。
其实这个算法就是把序列分为好几块,每一块满足:对于任意k,前k个数的和不会小于0(小于0就会分裂成两块了),当前i个数的和大于最大值时就进行更新,而最大值的左边界就是该块序列的第一个,右边界是第i个。
时间复杂度为O(n),而且可以一边读取一边处理,不需要开辟数组来存,空间也很省。
代码
#include<iostream>
using namespace std;
int main(){
int T;
cin >> T;
while(T--) {
int n, i, j;
cin >> n;
int *a = new int[n];
for(i=0;i<n;i++) cin >> a[i];
int maxsum = -99999;
int start=0, end=0;
for(i=0;i<n;i++){
int sum = 0;
for(j=i;j<n;j++){
sum += a[j];
if(sum>maxsum){
maxsum = sum;
start = i;
end = j;
}
}
}
cout << maxsum << " " << start+1 << " " << end+1 << endl;
delete []a;
}
return 0;
}
1010 Saving HDU
题目
Problem Description
话说上回讲到海东集团面临内外交困,公司的元老也只剩下XHD夫妇二人了。显然,作为多年拼搏的商人,XHD不会坐以待毙的。
一天,当他正在苦思冥想解困良策的时候,突然想到了自己的传家宝,那是公司成立的时候,父亲作为贺礼送来的一个锦囊,徐父当时交代,不到万不得已的时候,不要打开它。“现在不正是最需要的时候吗?”,一边想,XHD一边找到了这个精心保管的锦囊,打开一看,里面只有一句话“杭城北麓千人洞有宝”。
二话不说,XHD拿起一个大口袋就出发了,这个千人洞他是知道的,小的时候,爸爸曾经带他来过这个隐蔽的路口,并告诉他,这是千人洞。他现在才明白爸爸当初这句话的含义。
尽管有点印象,XHD还是花了很大的精力才找到这个异常隐蔽的洞口,走进一看,几乎惊呆了,真的是眼花缭乱!不过尽管宝贝的种类不少,但是每种宝贝的量并不多,当然,每种宝贝单位体积的价格也不一样,为了挽救HDU,现在请你帮忙尽快计算出来XHD最多能带回多少价值的宝贝?(假设宝贝可以分割,分割后的价值和对应的体积成正比)
Input
输入包含多个测试实例,每个实例的第一行是两个整数v和n(v,n<100),分别表示口袋的容量和宝贝的种类,接着的n行每行包含2个整数pi和mi(0<pi,mi<10),分别表示某种宝贝的单价和对应的体积,v为0的时候结束输入。
Output
对于每个测试实例,请输出XHD最多能取回多少价值的宝贝,每个实例的输出占一行。
Sample Input
2 2
3 1
2 3
0
Sample Output
5
经过锦囊相助,HDU会脱离危机吗?
欲知后事如何,且听下回分解——
题解
对单价降序排列,然后逐个获取总价,同时检测剩余体积够不够装
代码
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<queue>
using namespace std;
struct node{
int p;//单位体积的价格
int m;//此种类的总体积
} num[105];
bool cmp(node x,node y){
if(x.p==y.p)
return x.m>y.m;
return x.p>y.p;
}
int main(){
int V,N;
while(~scanf("%d",&V)&&V){
scanf("%d",&N);
for(int i=0; i<N; i++)
scanf("%d%d",&num[i].p,&num[i].m);
sort(num,num+N,cmp);
int result=0;
for(int i=0; i<N; i++){
if(V>=num[i].m){
result+=num[i].m*num[i].p;
V-=num[i].m;
}
else{
result+=V*num[i].p;
break;
}
}
printf("%d\n",result);
}
return 0;
}
这篇题解大部分是整理搬运,我自己有点来不及写完,所以我只是个搬运工,嘻嘻嘻