1 lowbit运算

$lowbit$运算：$lowbit(x)=x\&(-x)$，它的作用是取$x$的二进制最右边的1和它右边所有0。

整数在计算机中采用补码存储，$x$变为$-x$的过程就是按位取反后末位加1。二者与操作后就得到了$x$最右边的1和它右边所有0。$lowbit(x)$也可以理解为能整除$x$的最大2的幂次。

2 问题

给定一个包含$N$个元素的数组$A$，求它的区间$[i,j]$元素之和。最自然的想法是建一个前缀和的数组，然后做减法就可以求出任意区间和，时间复杂度$O(1)$，空间复杂度$O(n)$。

但是，如果对数组$A$进行更新，那我们就不得不再更新前缀和，就很麻烦。

树状数组可以很好地解决这个问题，它可以使得查询和更新的时间复杂度都变成$O(logn)$。

3 树状数组（Binary Indexed Tree, BIT）

树状数组与前缀和数组类似，是一个用来记录和的数组，不过它存的是在$i$号位之前（包含$i$号位）的$lowbit(i)$个整数之和。另外，树状数组的下标必须从1开始。如下图$C$数组，$C[i]$的覆盖范围是$lowbit(i)$。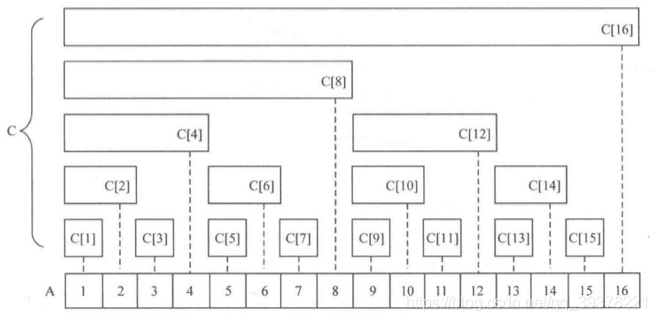

再结合下图就很容易理解了

3.1 单点更新与区间查询

为了解决刚才提出的问题，需要设计以下两个函数：

1. $getSum(n)$：返回前$n$个数的和$A[1]+\cdots +A[n]$
2. $update(n,v)$：实现将第$n$个数加上一个数$v$的功能，即$A[n]+=v$

先解决第一个函数，看几个例子：
$$\begin{gathered} A[1]+\cdots +A[14]=C[8]+C[12]+C[14] \\ A[1]+\cdots +A[11]=C[8]+C[10]+C[11] \end{gathered}$$
类似地，数组$A$的前$n$项和都可以由树状数组中的一些项的求和来表达，我们可以通过$lowbit$操作来找出这些项：

$$\begin{array}{rl}getSum(n)& =A[1]+\cdots +A[n]\\ & =A[1]+\cdots +A[n-lowbit(n)]+A[n-lowbit(n)+1]+\cdots +A[n]\\ & =getSum(n-lowbit(n))+C(n)\end{array}$$
这样就可以写出$getSum(n)$了：

//getSum返回前n个整数之和
int getSum(int n){
	int sum = 0;
	for (int i = n; i > 0; i -= lowbit(x)){
		sum += C[i];
	}
	return sum;
}

这样我们就可以通过$getSum(j)-getSum(i-1)$求区间$[i,j]$的和。这个过程就像不断向左上爬，如下图

然后看第二个函数，更新$A$中的一个值后如何对树状数组进行更新。还是先看例子，如果更新$A[6]$，我们要去找$C$中哪些项包含了$A[6]$，我们看上图，可以看到包含$A[6]$的有$C[6],C[8],C[16]$，放在上图中，就是寻找包含$A[6]$的那些矩形。
实际上这就是刚刚求和的逆操作，每次加上一个$lowbit$就可以得到下一个位置：

$$\begin{array}{rl}& C[6]:110\\ & C[8]:1000=6+lowbit(6)=110+10\\ & C[16]:10000=8+lowbit(8)=1000+1000\end{array}$$

这样就可以写出$update(n,v)$了：

void update(int n, int v){
	for(int i = n; i <= n; i += lowbit(i)){
		C[i] += v;
	}
}

这个过程就像不断向右上爬，如下图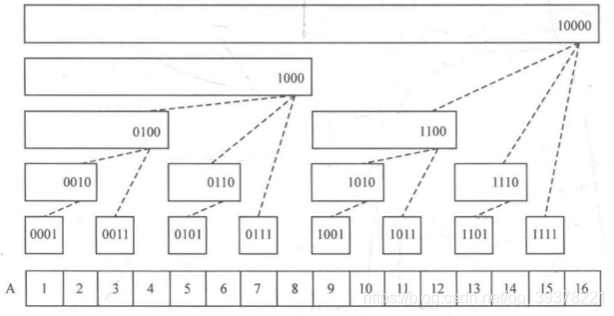

练习题

• leetcode 315.计算右侧小于当前元素的个数

4 参考资料

• 《算法笔记》第13章