接着上一次的卡方之后 ,我们来讲解t分布
1 t分布
设随机变量X与Y相互独立,且X服从标准正态分布N(0,1), Y服从自由度为n的卡方分布,则随机变量

的分布密度是 式1
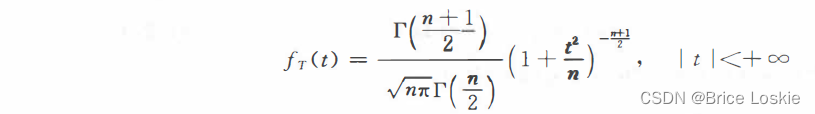
这种分布称为自由度为n的t分布,记作T~t(n).
证明过程我们不需要看 太过于繁琐 没有必要
我们直接记住结论就可以,之后我们会用到代码来推导
由式1不难看出,t分布的密度函数是偶函数,因此其密度曲线关于y轴对称,形状类似于正态分布,而且我们还可以证明式2
![]()
故当n很大时,t分布近似于正态分布N(0,1),但对于小的n,t分布与N(O,l)相差很大. 图1.4画出了n = 1,10, ∞时t分布的密度函数图形.
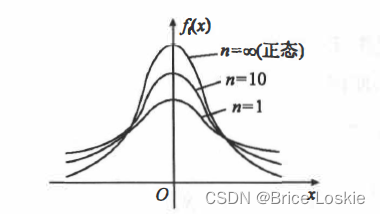
直接根据如上的函数写出的t分布的代码:
def gamma_function(n):
cal = 1
for i in range(2, n):
cal *= i
return cal
def student_t(x, freedom, n):
# divide [x.min(), x.max()] by n
x = np.linspace(x.min(), x.max(), n)
c = gamma_function((freedom + 1) // 2) \
/ np.sqrt(freedom * np.pi) * gamma_function(freedom // 2)
y = c * (1 + x**2 / freedom) ** (-((freedom + 1) / 2))
return x, y, np.mean(y), np.std(y)
for freedom in [1, 2, 5]:
x = np.arange(-10, 10) # define range of x
x, y, _, _ = student_t(x, freedom=freedom, n=10000)
plt.plot(x, y, label=r'$v=%d$' % (freedom))
plt.legend()
plt.show() 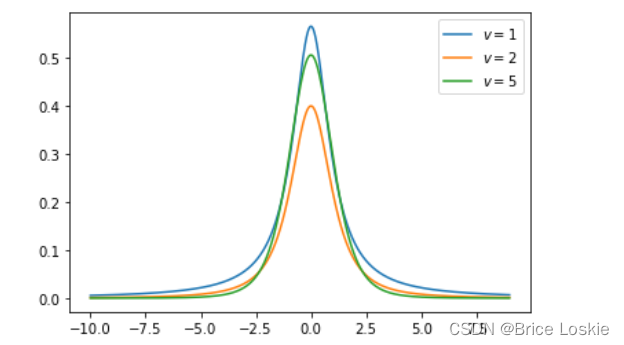
从原理来推导t分布

其中X服从正态分布
Y服从自由度为n的卡方分布
先求Y的数据
y=0
for i in range(5):
x=np.random.standard_normal(size=10000)
y=y+x*x
x=np.random.standard_normal(size=10000)
t=x/(np.sqrt(y/5))
plt.figure(figsize=(5,2),dpi=100)
plt.hist(t,1000)
plt.show()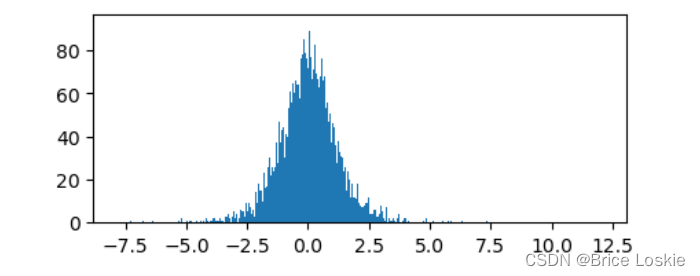
2 F分布

分布密度是

这个函数虽然看上去有点难,其实确实很难,但不要记啦 ,记也记不住,毕竟现在我连正态分布表达式都记不住
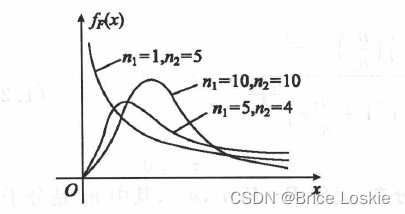
对于不同的自由度(n1,n2)及不同的数a(0<a<1) ,给出了满足等式
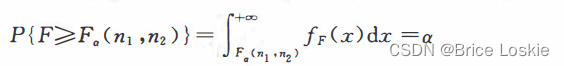
的上侧分位数
记住以下公式 可以和正态分布的
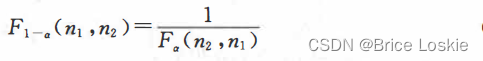
可以和正态分布的
形成对照记忆
版权声明:本文为fuxun222原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。