本文分成两个部分，一个部分来自于一本老的教科书，另一部分是我自己的个人笔记，不论哪个部分，都是在讲消元矩阵E。
教科书部分：
首先高斯消元的基本步骤就是用一个方程乘以一个系数得到一个新方程，然后再用另外一个方程减去这个新方程，就实现了消元。
例如下面这二元一次方程组，通过高斯消元法，把第二个方程中未知数x消去了。
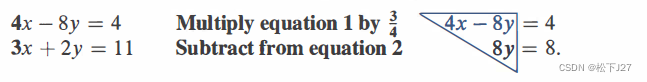
而事实上每一次的表达都能够通过矩阵的乘法来实现的。也就是说，把下图红框框中的文字表达，换成数学上的公式表达，也就是消元矩阵E（elimination matrix）也可以叫elementary matrix。
对于上面的这个方程组的这一操作而言，用消元矩阵E表达就是：
一般情况下，消元矩阵不会只用大写的E来表示，而是写成带下标的消元矩阵。他表示，第i行减去第j行的c倍，具体的常数c要根据实际情况而定(也表示把系数矩阵A中，i行j列处的元素变成0)。就本例来说，
=
,即第二行减去第一行的c倍。对矩阵A进行一次高斯消元，就好像是从Ax=b，变成了
(Ax)=
b。再比如，我们把消元矩阵
用在3x3的矩阵上，如下：
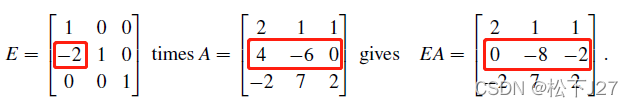
原始矩阵A通过乘以消元矩阵，得到了新矩阵
A，同时也完成了消元的操作。一定要注意这里消元矩阵E和A的乘法顺序，绝对不能颠倒。同时，如果E，A都是方阵，则二者的阶数必须相同。
对于一个nxn的方程组而言，高斯消元是需要很多步才能完成的，每一步都需要一个消元矩阵Eij，在实际消元的过程中，我们可以把这些Eij“合起来”。令连续个Eij的乘积的结果为矩阵X。这样一来，对Ax=b的消元，只需要用X分别乘以A和b就完成了。所以，我们可以非正式的说，矩阵X也是一种消元矩阵。
最后，每一个消元矩阵Eij都是可逆的。而他的逆的计算也非常方便，只需改变消元位置所对应的符号就行了，这在我自己的笔记中也有详细的说明。
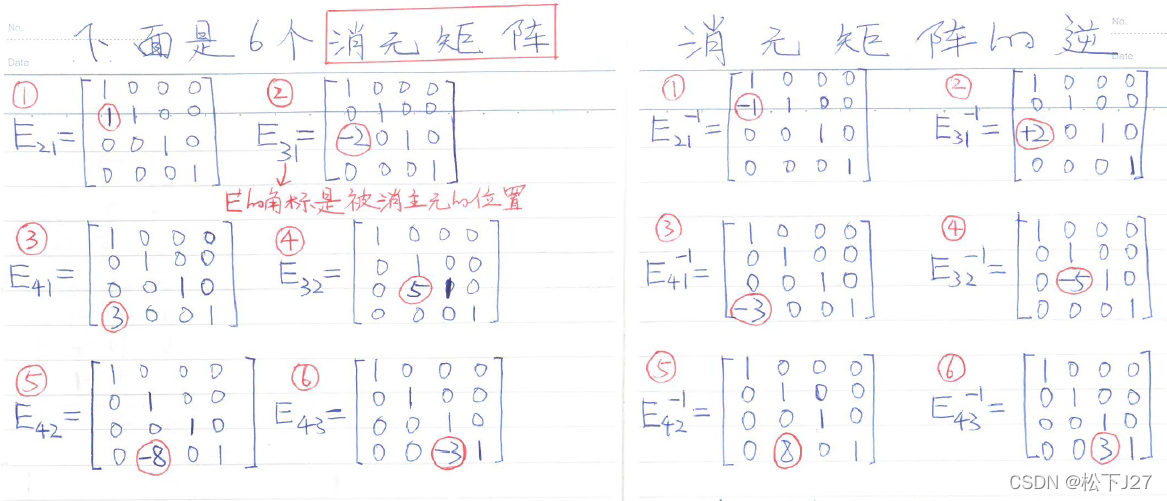
（图像上传的有点问题，点击图像就能看到原始画质的图像）
个人笔记部分：
三个基本矩阵
1，行交换（见下图E1）
2，某一行乘以一个常数（见下图E2）
3，某一行加上另外一行乘以一个常数 （见下图E3）
补充：
（全文完）
作者 --- 松下J27
鸣谢（参考资料）：
1，线性代数及其应用, 侯自新 南开大学1990
2，Linear Algebra and Its Applications,Gilbert strang
https://ccjou.wordpress.com/2010/02/02/%E7%89%B9%E6%AE%8A%E7%9F%A9%E9%99%A3-%E5%8D%81%EF%BC%9A%E5%9F%BA%E6%9C%AC%E7%9F%A9%E9%99%A3/
（配图与本文无关）
版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27