首先这是从左神视频里面出现的题目。
折纸问题:
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。例如:N=1时,打印: down N=2时,打印: down down up。
我现在这里说一下我自己的思路:
1、首先搞清楚为什么折痕会出现凹折痕和凸折痕,一张纸折叠第一次会出现一个折痕,这个定为凹折痕,第二次折叠时我们假定吧纸中间连接处分开,就相当于直接折叠两张纸,所以会出现两个折痕,但是上面那张纸它的方向是反的,所以上面那张纸的凹折痕放下来就变成了凸折痕。画个图说明一下。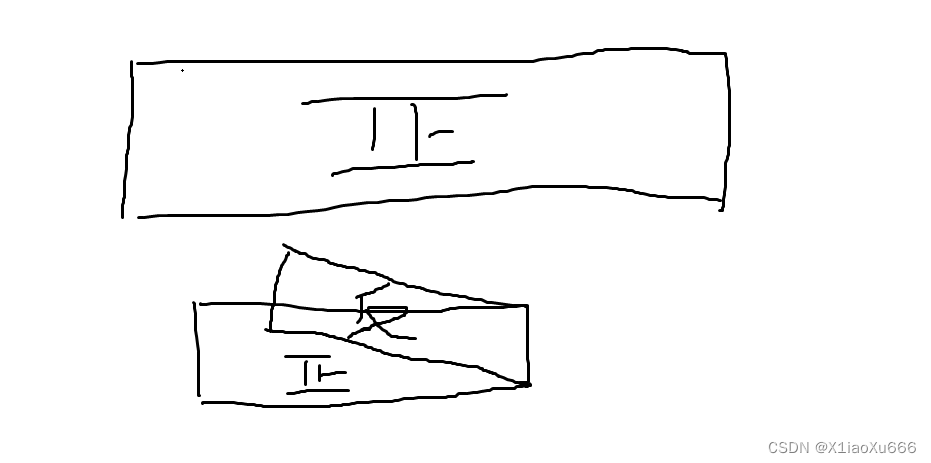
2.弄懂折叠几次会出现几个折痕。从上述分析中很轻易的可以得出,每折叠一次纸的层数会乘二,所以新增的折痕数也是乘二的,得出折痕数和折纸次数的关系为2的n次方-1。
3,开始分析折痕出现规律。一张正面的纸折一次会出现一个凹折痕,变成正反两张纸,它的下一轮折叠就变成了凹凸两道折痕,并且分布在原折痕左右两侧,而一张反的纸折一次会出现一个凸折痕,变反正两张纸,它的下一轮折叠就是凸凹两道折,也是分布在左右两侧。这种一个折痕再次折叠出现两个新折痕的样子很像二叉树结构,在这里将纸每次折叠出现的新折痕看成它的两个左右节点,左边的看成它的左节点,右边的看成它的右节点。
4,我们进一步分析凹凸折痕出现顺序规律,首先我们能确定的是不管凹凸折痕,它下一次折叠新出的折痕必然是凹凸两种折痕,且正面的纸出现的折痕是凹凹凸,反面的纸出现的折痕是凸凸凹,但是反面的纸最后我们计算顺序的时候是要翻折过来的,所以变成了凹凸凸,分析到这可以得出结论,一个折痕翻折出现的新折痕一定是左边是凹右边是凸,对应二叉树一个父节点的左节点为凹右节点为凸。而且遍历顺序是左中右,刚好对应上二叉树的中序遍历,折痕出现规律分析完毕。
5.结合述分析得出二叉树整体结构(根节点为凹是确定的),又得出遍历顺序即可解出答案,下面附上代码。
/// <summary>
/// 二叉树结构
/// </summary>
/// <typeparam name="T"></typeparam>
public class TreeNode<T>
{
public T value;
public TreeNode<T> left;
public TreeNode<T> right;
public TreeNode<T> parent;
public TreeNode(T value)
{
this.value = value;
}
}public string GetMark(int n)
{
if (n == 0) return null;
string ans = "";
TreeNode<bool> head = new TreeNode<bool>(true);
Queue<TreeNode<bool>> queue = new Queue<TreeNode<bool>>();
queue.Enqueue(head);
int i = 1;
while (i < Math.Pow(2, n - 1))//构建出二叉树
{
var node = queue.Dequeue();
node.left = new TreeNode<bool>(true);
node.right = new TreeNode<bool>(false);
queue.Enqueue(node.left);
queue.Enqueue(node.right);
i++;
}
Stack<TreeNode<bool>> stack = new Stack<TreeNode<bool>>();
while (stack.Count != 0 || head != null)//中序遍历
{
if (head != null)
{
stack.Push(head);
head = head.left;
}
else
{
head = stack.Pop();
ans += head.value ? "down " : "up ";
head = head.right;
}
}
return ans;
}总结:我是构出整个二叉树,再进行中序遍历得出结果的,B站左神的代码更加精炼,有兴趣的可以去看看。