1、booth算法定义
将乘数看作从最低位开始的一串二进制数字。Booth算法的基本思路是:对于具有连续0和1的组,需要产生的部分积较少。对于乘数中每个0,仅需要将前面的累加的部分积向右移动一位。
布斯编码采用相加和相减的操作计算补码数据的乘积,可以减少部分积的数目,用来计算有符号乘法,提高乘法运算的速度。
2、二进制乘法过程
二进制乘法过程可仿照十进制数乘法进行。由低位到高位,用乘数的每一位去乘被乘数,若乘数的某一位为1,则该次部分积为被乘数;若乘数的某一位为0,则该次部分积为0。某次部分积的最低位必须和本位乘数对齐,所有部分积相加的结果则为相乘得到的乘积。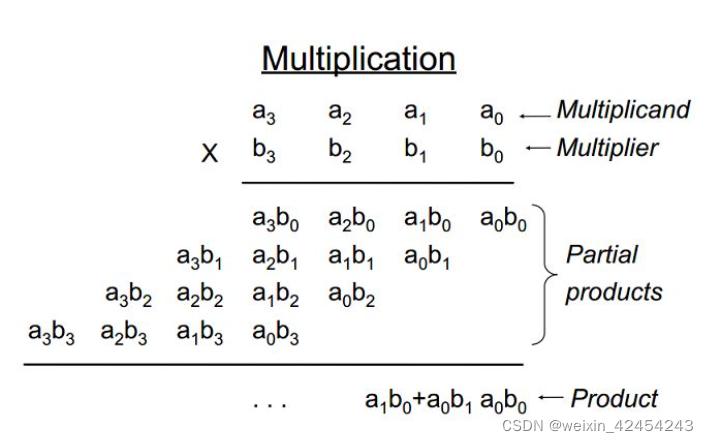
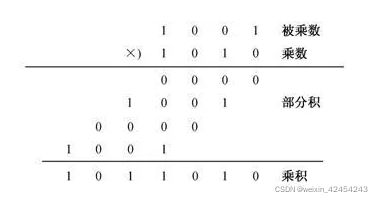
上诉例子我们知道乘数和被乘数的位数都是4,那么如果计算结果超过2n(n)为二进制表示位数,那么我们将2n高位的其他位省略。
3、二进制乘法转换成 booth乘法运算
例如假设有一个8位乘数(Multiplier):0011_1110,它将产生6行非零的部分积。如果把该数字记成另一种形式,0100_00(-1)0(可以验证是同一个数字,-1是负1)
二进制化为十进制
0011_1110 = 0*2^7 + 0*2^6 + 1*2^5 + 1*2^4 + 1*2^3 + 1*2^2 + 1*2^1 + 0*2^0 = 62
0100_00(-1)0 = 0*2^7 + 1*2^6 + 0*2^5 + 0*2^4 + 0*2^3 + 0*2^2 + (-1)*2^1 + 0*2^0 = 64 -2 = 62
注:64=2^6 2=2^1
0011_1110 = 0100_00(-1)0 = 2^6-2^1=0100_0000 - 0000_0010
计算0010_0001×0011_1110,在这里可以首先将乘数0011_1110改写为0100_0000 - 0000_0010,即根据乘法分配律得:
0010_0001×0011_1110
= 0010_0001×(0100_0000 - 0000_0010)
此时,对于乘数,我们需要计算6次的部分积,变成了计算两次部分积。
4、Radix-2 Booth乘法器
Radix-2 Booth乘法器,即是基2 Booth乘法器,基为2的一次方。
2 = 2^1
数的表示方法: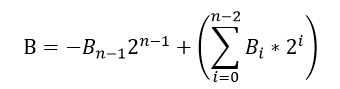
N比特数B,将其展开,在N比特数B的最后一位B0后添加一个辅助位B(-1),且B(-1)=0: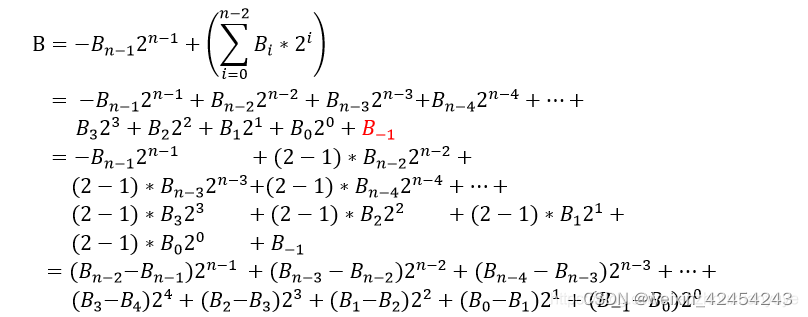
从上式中得出,其基系数为: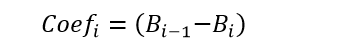
将A与B相乘,则: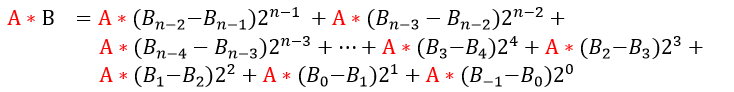
对于B的第n位和第n-1位,从上式可以发现,B可以通过相邻比特位的减法和2的n次方相乘而得。如果AB两数相乘,从B的-1和0位逐次向高位检查,累积A*B的结果。
根据 基2 Booth乘法器的基系数 表达式,得出以下Booth4编码:
相邻两个数据位,进行公式(第0位)-(第1位)计算,得到两位的编码(相邻居两位,从后面像前面减)
00 0-0= 0 转化成二进制编码 0
01 1-0= 1 转化成二进制编码 1
10 0-1=-1 转化成二进制编码-1
11 1-1= 0 转化成二进制编码 0
根据两个数据位的编码决定进行加法、减法还是仅仅移位操作。
以下是基2 Booth编码表,根据两个数据位的编码决定进行加法、减法还是仅仅移位操作。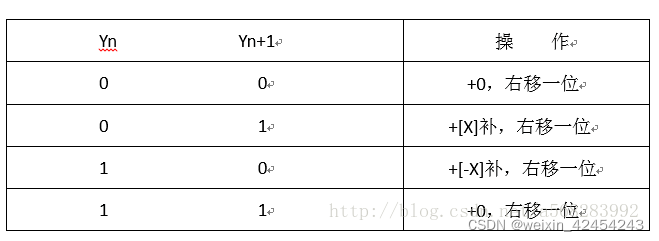
5、Radix-4 Booth乘法器
Radix-4 Booth乘法器,即是基4 Booth乘法器。基为2的二次方。
4 = 2^2
数的表示方法: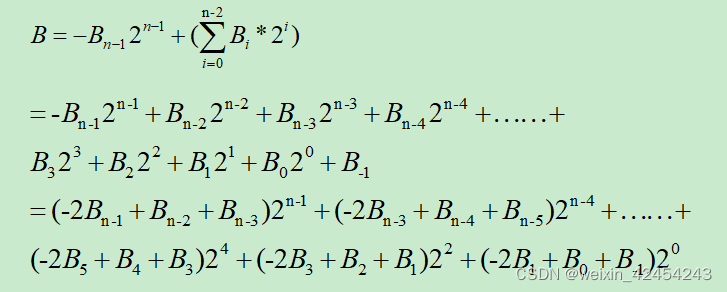
从上式中得出,基4 Booth乘法器的基系数为: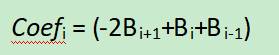
将A与B相乘,则: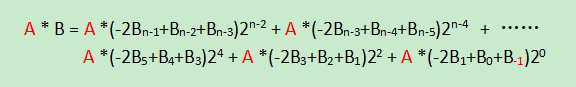
根据 基4 Booth乘法器的基系数 表达式,得出以下Booth4编码:
相邻3位数,进行公式-2*(第3位)+(第2位)+(第1位)计算,得到两位的编码(相邻居两位,从后面像前面减)
000 (-2)*0+0+0= 0 转化成二进制编码 00,即 +0
001 (-2)*0+0+1= 1 转化成二进制编码 01,即 +1
010 (-2)*0+1+0= 1 转化成二进制编码 01,即 +1
011 (-2)*0+1+1= 2 转化成二进制编码 10,即 +2
100 (-2)*1+0+0=-2 转化成二进制编码-10,即 -2
101 (-2)*1+0+1=-1 转化成二进制编码-01,即 -1
110 (-2)*1+1+0=-1 转化成二进制编码-01,即 -1
111 (-2)*1+1+1= 0 转化成二进制编码 00,即 -0
以下是基4 Booth编码表,其中A为被乘数,B为乘数。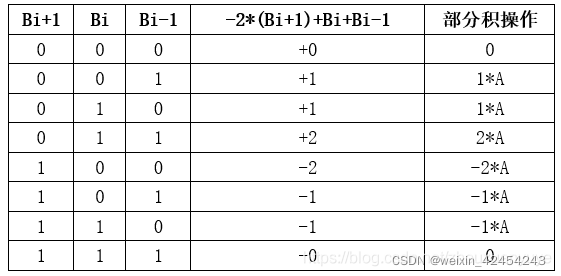
6、Booth乘法器计算实例
下面展示一些 内联代码片。
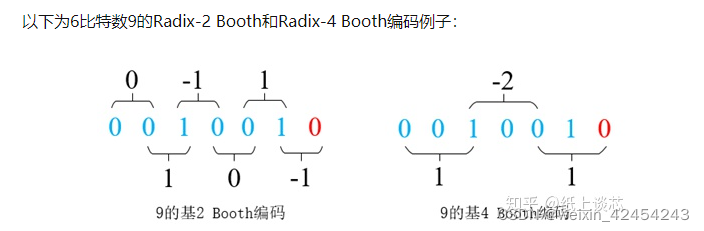
从二进制看9:(共6步)
9 = 0*2^5 + 0*2^4 + 1*2^3 + 0*2^2 + 0*2^1 + 1*2^0
从基2看9:(共6步)
9 = 0*2^4 + 1*2^4 + (-1)*2^3 + 0*2^2 + 1*2^1 + (-1)*2^0
从基4看9:(共3步)
9 = 1*4^2 + (-2)*4^1 + 1*4^0
= 1*2^4 + (-2)*2^2 + 1*2^0
其阵列表示如下: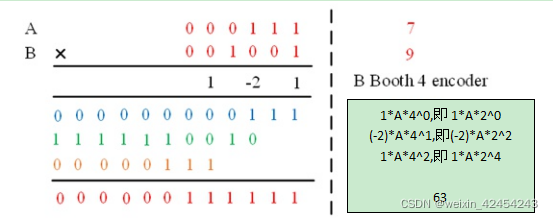
注意:算式绿色部分的计算
(-2)*A*4^1
步骤1 4^1 = 2^2(转化成2的偶次方)表示结果算术左移两位
步骤2 (-2)*A=[(-1)*A]*2^1
步骤2.1 2^1表示在基2中表示结果向左移1位
步骤2.2 (-1)*A表示加上(-A);此例题中A=000111,(-A)=~(100111)+1=111000+1=111001
所以将结果11_1001在基2中表示结果向左移1位,得到111_0010,乘积的位数为2*6位,前面符号位补齐
此处引用 https://zhuanlan.zhihu.com/p/143802580.
例如第2章节的例题:计算0010_0001×0011_1110(即为33×62=2046),分别按照基2和基4展开运算
在这里可以首先将乘数0011_1110按照基2展开为
0011_1110——0 相邻两位 首位分组为 0(0)*2^0 + 1(0)*2^1 + 1(1)*2^2 + 1(1)*2^3 + 1(1)*2^4 + 1(1)*2^5 + 0(1)*2^6 + 0(0)*2^7
括号中的后一位减去前一位
0011_1110 = (0-0)*2^0 + (0-1)*2^1 + (1-1)*2^2 + (1-1)*2^3 + (1-1)*2^4 + (1-1)*2^5 + (1-0)*2^6 + (0-0)*2^7
= (-1)*2^1 + 1*2^6 //= (-2) + 64 = 62
= (-1)*0000_0010 + 0100_0000
0010_0001*0011_1110 = 0010_0001*(0100_0000 - 0000_0010)
= 0010_0001*0100_0000 -0010_0001*0000_0010 //进行移位计算,-0010_0001的补码为1101_1111,8*8位宽度为16位,前面符号为补齐
= 00_0010_0001_000000 + 1101_1111*0000_0010 //进行移位计算
= 0000_1000_0100_0000 + 1111_111_1101_1111_0
= 0000_1000_0100_0000 + 1111_1111_1011_1110
= 1_0000_0111_1111_1110 //因为两个8位数相乘,结果为16位,超出位舍去
所以,最后结果为: 111_1111_1110=2046
在这里可以首先将乘数0011_1110按照基4展开为
0011_1110——0 相邻三位 首位分组为 10(0)*4^0 + 11(1)*4^1 + 11(1)*4^2 + 00(1)*4^3
相邻3位数,进行公式-2*(第3位)+(第2位)+(第1位)计算
0011_1110 = (-2)*4^0 + (-0)*4^1 + (-0)*4^2 + (1)*4^3
= (-2)*4^0 + (1)*4^3
= (-1)*2^1 + 1*2^6 //= (-2) + 64 = 62
= (-1)*0000_0010 + 0100_0000
0010_0001*0011_1110 = 0010_0001*(0100_0000 - 0000_0010)
= 0010_0001*0100_0000 -0010_0001*0000_0010 //进行移位计算,-0010_0001的补码为1101_1111,8*8位宽度为16位,前面符号为补齐
= 00_0010_0001_000000 + 1101_1111*0000_0010 //进行移位计算
= 0000_1000_0100_0000 + 1111_111_1101_1111_0
= 0000_1000_0100_0000 + 1111_1111_1011_1110
= 1_0000_0111_1111_1110 //因为两个8位数相乘,结果为16位,超出位舍去
所以,最后结果为: 111_1111_1110=2046
乘法器的布斯算法原理与VERILOG实现
booth4与csa4:2等见: https://zhuanlan.zhihu.com/p/127164011.
Verilog编程之乘法器的实现: https://blog.csdn.net/weixin_43074474/article/details/90473709.
备注:该内容为读书笔记,部分内容与图片收集来源于网络,如有侵权或错误,请联系我整改,谢谢!