旋转矩阵公式生成器_没那么简单——说说旋转（1）

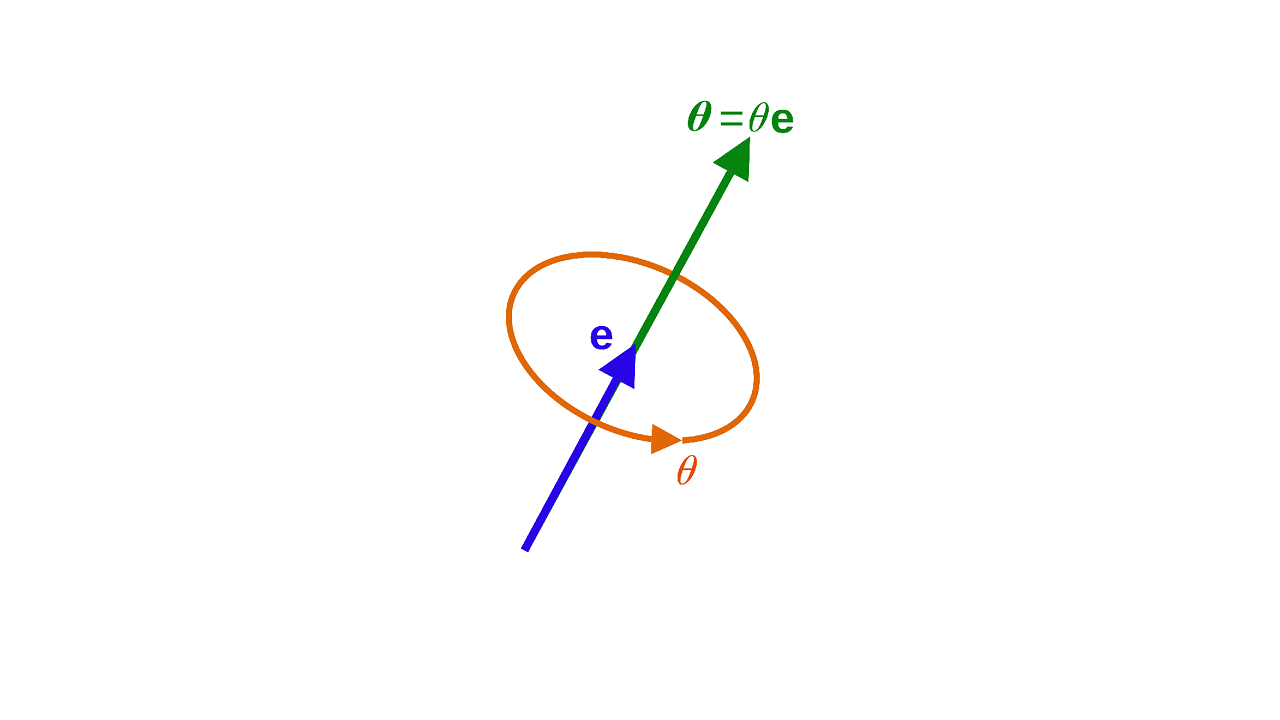
0. 楔子

之所以写这篇文章，是之前在调研文献的过程中，经常会遇到关于旋转的概念，公式等，比如旋转矩阵、轴-角表示(axis-angle representation)、四元数、李群、李代数等等。

在调研过程中，我深深地感到，目前缺乏对上述这些内容的一些友好、直观的introduction。我本人不是搞数学的，甚至数学还相当菜，但我还是感觉research，re-search，其实就是sort things out & make things simple。所以想在这里总结一些内容，有不对的，希望大家能帮忙指出，至少我们可以把这些概念搞清楚。

那么在正式开始之前，我们先过一些基本的概念，这些概念后续会直接使用，不会再提及。

设我们有两个向量

,

假设这俩是三维向量吧，方便后面我们聊叉积。那么有

，

。那么两个向量的

那么两个向量的叉积，是另外一个新的向量。

的方向垂直于两个输入向量张成的平面，朝向由右手定则确定，即四指方向从

向量转向

向量，大拇指方向指向

。

的大小为

。在三维条件下，有一个比较简单的式子帮助我们快速得到叉积结果：

OK，实际上如果我们把上面的辅助变量i, j, k去掉的话，那么叉积可以定义为：

这里介绍一种后面经常用到的数学工具，叫作反对称矩阵算子（skew-symetric operator），有多种记法，我们统一记作

。所以叫它反对称算子，是因为有

。

什么意思呢？就是说给你一个向量

，这个算子

按照如下方式，

：

如果我们再仔细看一下上面叉乘的定义就会明白这个算子的深意了：

用这个算子，可以将不直观、不好算的向量叉乘，转化为，直观、好算的矩阵乘法。

1. 说说旋转矩阵

说起旋转矩阵，大家都太熟了，简单，旋转矩阵肯定是正交阵，

。行列式方面：

。所有行向量组成一个正交空间的基，所有列向量组成一个正交空间的基。

只能说，性质也太好了吧。

这边搬运一下《视觉SLAM十四讲》里面关于旋转矩阵导出的一段描述，个人认为是旋转矩阵最简单直观的导出。

首先设在三维空间里面，我们有一个最常用的标准正交基

，其中

，

，

。简单对吧，就是

轴，

轴，

轴的一个单位向量。

那么假设有一个向量

，那么这里面

实际上是这个向量在我们刚才常用基

下面的

OK，那么假如说，

通过旋转转到了

。那其实就相当于我们的常用基坐标系，进行了一个

。

呢，实际上就想到与同一个向量

在新坐标系

下面的坐标（这个大家可以自己搞个2D版的例子自己试一下）。

根据书上写的，我们有：

，

如果这个时候我们左边乘以一个

的转置：

因为是标准正交基对吧，所以有：

也就是咱们熟悉的：

。

顺着这个思路，刚刚的正交性质啊，行列式性质啊，其实都十分直观。给我的感觉，就是旋转矩阵，其实就是两个标准正交基的一个外积。因为本身标准正交基就具有十分好的性质，所以呢，旋转矩阵具有良好性质，本身也是一件合情合理的事情了。

2. Rodrigues' formula

主要是搬运维基百科的一点东西，这公式很重要，需要总结一下。

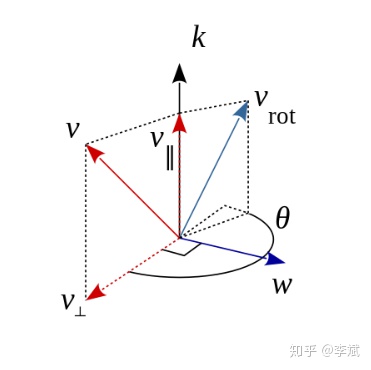
OK，还是先说设定我们有一个向量

，现在绕

做

角度的旋转，那么

应该等于什么呢？

首先对向量

做一个分解：

。也就是跟轴

平行及垂直的两个分量。那么平行分量简单地通过投影就可以得到：

。后面的部分代表方向，前面的括号代表长短。垂直分量稍微麻烦一点，需要用到之前介绍过的叉积，这边最好注意一下右手定则以及符号：

看一下图，再看一下红色部分，

和

叉完以后是图里面的

向量。

再和

叉积，叉完以后按右手定则应该是

的反方向。

好了，下面的就是平行分量不转，垂直分量转

角。这是一个2D旋转，如果我们以

和

为坐标轴建系，那么：

准备工作基本做好了，我们现在可以得到第一版本，向量点积叉积版的罗格里格斯公式：

OK，目前看起来一切都好，不过叉积还不太好算，我们利用之前介绍的反对称算子

进行进一步的化简，由之前的推导，我们有：

再往前走一步：

那么我们重新推导第二版，反对称算子版本，也就是矩阵乘法版本的罗德里格斯公式：

又因为：

，所以：

这也是我们最常见到的Rodrigues公式的版本，这里面还藏着个玄机，其实就是罗德里格斯公式就是轴-角表示法（axis-angle）和旋转矩阵的一个转换。当然也可以看成是

和

的一个相互转换。我们后面会提到。

第一篇先写到这儿吧。