✅ 在学《计算机网络与通信》时,深入探讨并总结了 “信道利用率” 这个重点,做了一点笔记
个人简介:南京邮电大学,计算机科学与技术,在读本科
兴趣领域:数据结构、C/C++
文章目录
一、信道利用率的概念
● 信道利用率:指发送方在一个发送周期的时间内,发送有效数据所需要的时间占整个发送周期的比率。
◆ 例如:发送方从一开始发送数据,到收到第一个确认帧为止,称为一个发送周期 T TT。发送方在这个周期内共发送 L LL 比特的数据,发送方的传输速率为 C CC,则发送方用于发送有效数据的时间为 L / C L/CL/C。则在这种情况下,信道的利用率为 η = L / C T η=\frac{L/C}{T}η=TL/C。
● 上述中 L LL 和 C CC 都好理解,一般题目都会直接给。但发送周期 T TT 就不是直接给的了,需要我们就 某种协议 而计算了。
二、停止-等待协议的信道利用率怎么算?
2.1 停止-等待协议——概念
● 停止-等待协议: 发送窗口和接收窗口大小均为 1,发送方每发送一帧之后就必须停下来等待接收方的确认返回,仅当接收方确认正确接收后再继续发送下一帧。
● 为了写出其信道利用率,先了解一下 8 个重要的时间节点,即下图所示的 t 0 、 t 1 、 . . . 、 t 7 t_0、t_1、...、t_7t0、t1、...、t7:
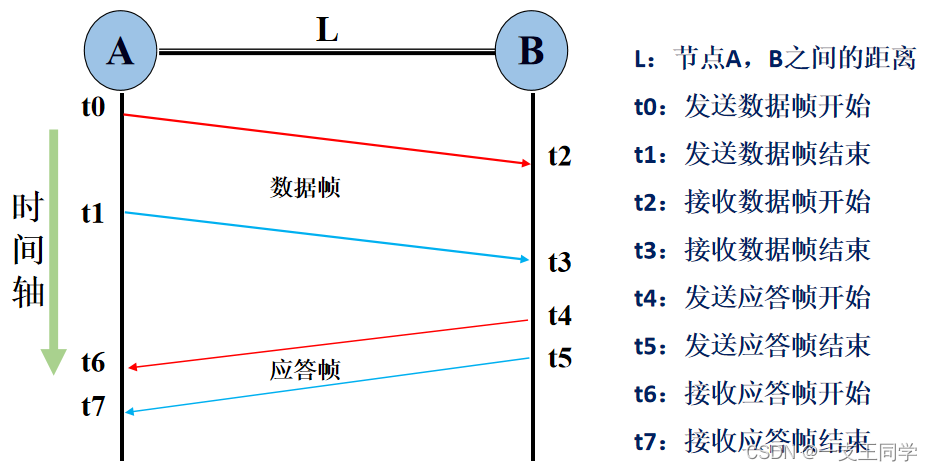
● 数据帧长度: F = H + D F=H+DF=H+D,注:H HH 为帧头(用于传输控制、检验等),D DD 为数据。
● 发送时延: t F = t 1 − t 0 = t 3 − t 2 = F / C t_F = t_1 - t_0 = t_3 - t_2 = F / CtF=t1−t0=t3−t2=F/C,注:C CC 为发送方的传输速率。
● 有效的发送时延: t D = D F × t F t_D = \frac{D}{F}\times t_FtD=FD×tF
● 传播时延: t P = t 2 − t 0 = t 3 − t 1 = L / v t_P = t_2 - t_0 = t_3 - t_1 = L/vtP=t2−t0=t3−t1=L/v,注:L LL 为节点 A 与 B 之间的距离、v vv 为信号传播速率(常为3×108m/s)。
● 处理时延: t p r o c = t 4 − t 3 t_{proc}= t_4 - t_3tproc=t4−t3
● 应答帧发送时延: t A = t 5 − t 4 = t 7 − t 6 = A / C t_A = t_5 - t_4 = t_7 - t_6= A / CtA=t5−t4=t7−t6=A/C,注:A AA 为应答帧长度。
●在正常情况(即无差错)下,停止-等待协议的 信道利用率 为:
η = t 1 − t 0 t 7 − t 0 = t D t F + t A + 2 t P + 2 t p r o c η =\frac{ t_1-t_0}{ t_7-t_0}=\frac{ t_D}{ t_F + t_A + 2t_P + 2t_{proc}}η=t7−t0t1−t0=tF+tA+2tP+2tproctD
◆ 注:为什么是两倍的 t p r o c t_{proc}tproc 因为我们认为发送方在接收到 应答帧 后,也会需要一定处理时间(图中未画,即 t 8 t_8t8,所以严谨来说 η = t 1 − t 0 t 8 − t 0 η =\frac{ t_1-t_0}{ t_8-t_0}η=t8−t0t1−t0)。
● 别看上面那个公式这么大一堆,其实在实际题目当中,已隐去很多细节。
● 假设收发双方处理时间相同,即不用考虑 处理时延t p r o c t_{proc}tproc 、 传播时延t P t_PtP 以及 应答帧发送时延t A t_AtA 的开销,则信道利用率 η ηη 仅与帧结构相关:
η = t D t F = D F = D H + D η= \frac{t_D} { t_F} = \frac{D}{F} = \frac{D}{H+D}η=tFtD=FD=H+DD
● 一般在考试中,若题目没有特殊说明,我们只用考虑 发送时延t F t_FtF、传播时延t P t_PtP:η = t F t F + 2 t P η= \frac{t_F} { t_F+2t_P}η=tF+2tPtF
● 另外,在非正常情况(即出现差错,需要重发若干次)下,停止-等待协议的 信道利用率 为:
η = t D ( t F + t A + 2 t P + 2 t p r o c ) × 1 个 帧 的 平 均 传 送 次 数 = t D ( t F + t A + 2 t P + 2 t p r o c ) × ( 1 + 1 个 帧 的 平 均 重 传 次 数 ) η =\frac{ t_D}{ (t_F + t_A + 2t_P + 2t_{proc}) \times1个帧的平均传送次数 } = \frac{ t_D}{ (t_F + t_A + 2t_P + 2t_{proc}) \times(1+1个帧的平均重传次数) }η=(tF+tA+2tP+2tproc)×1个帧的平均传送次数tD=(tF+tA+2tP+2tproc)×(1+1个帧的平均重传次数)tD
2.2 停止-等待协议——优缺点
● 停止-等待协议的优点:控制过程比较简单,易于实现 。
● 停止-等待协议的缺点:通信信道的利用率不高,信道还远远没有被所传输的数据比特填满。
2.3 停止-等待协议——例题
● 例1. 信道速率为 8 kb/s,采用停止等待协议,传播时延 t p t_ptp 为 20 ms,确认帧长度和处理时间均可忽略,问帧长为多少才能使信道利用率达到至少 50%?
解:
因为信道利用率:η = t s t s + 2 t p ≥ 50 % η =\frac{ t_s}{ t_s +2 t_p} ≥ 50\%η=ts+2tpts≥50%,而 t p = 20 m s t_p = 20\, mstp=20ms,故 t s ≥ 40 m s t_s≥40msts≥40ms
设帧长为 L LL bit,则发送时延 t s = L b i t 8 K b / s ≥ 40 m s t_s = \frac{L \,bit}{8 Kb/s}≥40msts=8Kb/sLbit≥40ms,解得:L ≥ 320 b i t L≥320\, bitL≥320bit
故帧长 L LL 应大于等于 320 bit。
● 例2. 在卫星通信系统中,两个地面卫星通信站之间利用卫星的转发技术进行通信,信号从一个地面站经卫星传到另一个地面站,若设其传播时延为 250 ms,发送一个数据帧的时间为 20 ms,试分析此系统的信道利用率。
【注:由于卫星距离地面较远,电磁波需要较长时间才能从一个地面站传播到另一个。在卫星通信中,从一个地面站经过卫星到另一个地面站,称为一“跳”。】
解:
信号从一个地面站经卫星传到另一个地面站,其传播时延为 250 ms,发送一个数据帧的时间为 20 ms.
则从发送站开始发送到数据帧被目的站接收,一共需要时间 20ms + 250ms = 270ms
(因为题目中没说,则) 不考虑 目的站对接收到的 数据帧的处理时间 和 应答帧的发送时间 (可以认为应答帧非常短),也不用考虑 帧头(用于传输控制、检验等)
则应答帧也需要经过 250ms 才能被发送站接收到。
从发送第一帧开始,到收到应答所需要的时间为:270ms + 250ms = 520ms
则此系统的信道利用率为: η = 20 m s 520 m s ≈ 4 % η =\frac{ 20\, ms}{ 520\, ms}≈ 4%η=520ms20ms≈4%
◆ 从例 2 不难看出:对于 “停止-等待协议”,由于大量时间用于等待,因此系统利用率很低,造成资源的浪费。
三、回退N帧的 ARQ 协议的信道利用率怎么算?
3.1 回退N帧的 ARQ 协议——概念
● 回退N帧的 ARQ 协议(Go-Back-N,即GBD):发信侧不用等待收信侧的应答,持续的发送多个帧,假如发现已发送的帧中有错误发生,那么从那个发生错误的帧开始及其之后所有的帧全部再重新发送。这种协议也称为 “连续 ARQ 协议” 或 “全部重发协议”。
● 为了写出其信道利用率,先了解一下 16 个重要的时间节点,即下图所示的 t 0 、 t 1 、 . . . 、 t 15 t_0、t_1、...、t_{15}t0、t1、...、t15:【假设其发送的滑动窗口为 3、接收窗口的大小为 1 】
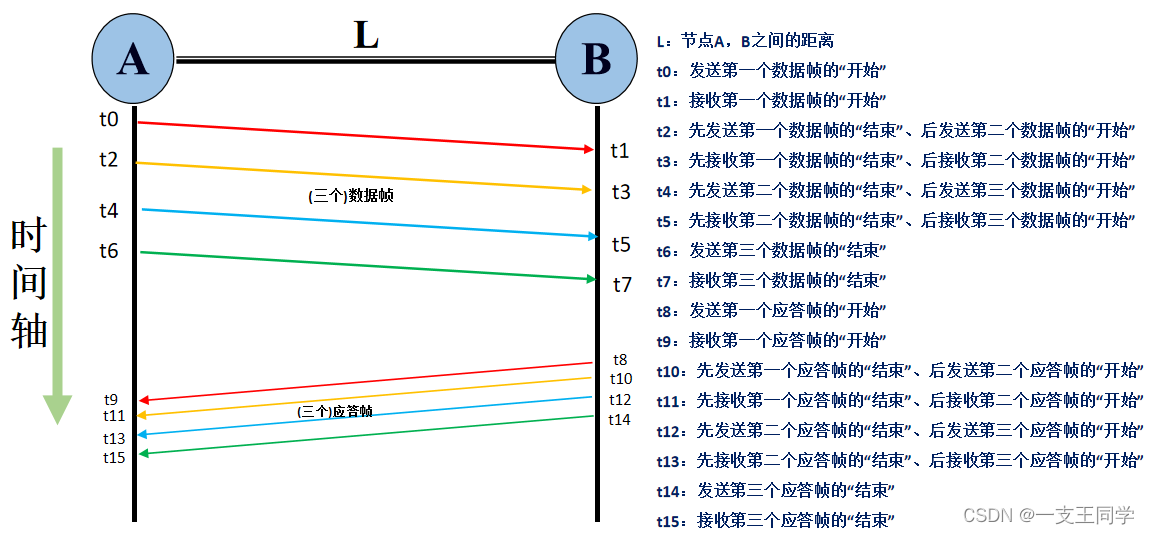
● 发送窗口的大小: W T W_TWT,右上图可知:W T = 3 W_T=3WT=3
● 数据帧长度: F = H + D F=H+DF=H+D,注:H HH 为帧头,D DD 为数据。
● 发送时延: t F = t 2 − t 0 = t 4 − t 2 = t 6 − t 4 = F / C t_F = t_2 - t_0 = t_4 - t_2 = t_6 - t_4= F / CtF=t2−t0=t4−t2=t6−t4=F/C,注:C CC 为发送方的传输速率。
● 有效的发送时延: t D = D F × t F t_D = \frac{D}{F}\times t_FtD=FD×tF
● 传播时延: t P = t 1 − t 0 = t 3 − t 2 = L / v t_P = t_1 - t_0 = t_3 - t_2 = L/vtP=t1−t0=t3−t2=L/v,注:L LL 为节点 A 与 B 之间的距离、v vv 为信号传播速率(常为3×108m/s)。
● 处理时延:t p r o c = t 8 − t 3 = t 10 − t 5 t_{proc}= t_8 - t_3 = t_{10}-t_5tproc=t8−t3=t10−t5,注意与 “停止-等待协议” 的处理时延相对比。
● 应答帧发送时延: t A = t 10 − t 8 = t 12 − t 10 = t 14 − t 12 = A / C t_A = t_{10} - t_8 = t_{12} - t_{10} = t_{14} - t_{12} = A / CtA=t10−t8=t12−t10=t14−t12=A/C,注:A AA 为应答帧长度。
● 在正常情况(即无差错)下,回退N帧的 ARQ 协议的 信道利用率 为:
η = W T × t D t F + t A + 2 t P + 2 t p r o c η =\frac{W_T \times t_D}{ t_F + t_A + 2t_P + 2t_{proc}}η=tF+tA+2tP+2tprocWT×tD
● 也别看上面那个公式这么大一堆,其实在实际题目当中,已隐去很多细节。
● 假设收发双方处理时间相同,即不用考虑 处理时延t p r o c t_{proc}tproc 和 应答帧发送时延t A t_AtA 的开销,则信道利用率 η ηη 仅与帧结构相关:
η = W T × t D t F + 2 t P η= \frac{W_T \times t_D} { t_F + 2t_P}η=tF+2tPWT×tD
● 另外,在非正常情况(即出现差错,需要重发若干次)下,回退N帧的 ARQ 协议的 信道利用率 为:
η = W T × t D ( t F + t A + 2 t P + 2 t p r o c ) × 1 个 帧 的 平 均 传 送 次 数 = W T × t D ( t F + t A + 2 t P + 2 t p r o c ) × ( 1 + 1 个 帧 的 平 均 重 传 次 数 ) η =\frac{ W_T \times t_D}{ (t_F + t_A + 2t_P + 2t_{proc}) \times1个帧的平均传送次数 } = \frac{ W_T \times t_D}{ (t_F + t_A + 2t_P + 2t_{proc}) \times(1+1个帧的平均重传次数) }η=(tF+tA+2tP+2tproc)×1个帧的平均传送次数WT×tD=(tF+tA+2tP+2tproc)×(1+1个帧的平均重传次数)WT×tD
◆ 有人可能会问,为啥只用 W T W_TWT 去乘 t D t_DtD,而不去乘 t F t_FtF?
这是因为对于 发送周期T TT 而言,定义上考虑的是从 “有效发送第一个数据帧的开始” 到 “有效接收第一个应答帧的开始” 这段时间。而且,实际生活中,处理时延t p r o c t_{proc}tproc 并没有上图中那么大,所以看上去可能会产生一种视觉上的 “误会”。如果忽略了 t p r o c t_{proc}tproc 的话,应该是下面这张图的样子:【注意,图中的 t S t_StS 即 t F t_FtF,只不过往往考试题目会忽略 “帧头” 和 t A t_AtA,所以常常是 η = W T × t S t S + 2 t P η= \frac{W_T \times t_S} { t_S + 2t_P}η=tS+2tPWT×tS← 重点掌握公式】

3.2 回退N帧的 ARQ 协议——优缺点
● 回退N帧的 ARQ 协议的优点:允许发送方在等待应答的同时,能够连续不断地继续发送数据帧(而不必每一帧都是接收应答后才可以发送下一帧),提高了传输效率,还能满足流量控制、差错控制等数据链路层的基本要求。
● 回退N帧的 ARQ 协议的缺点:如果传输中某一帧出现了差错,则后续帧即使正确传送到接收方,也会被丢弃。发送发必须从出错的帧开始,全部重传。这种处理方式比较简单,但对已经正确传输的数据帧重传,降低了通信效率。
◆ 对于它的缺点,这里放一张图来简单说明吧:【需要注意的是 ACK 也有序号】
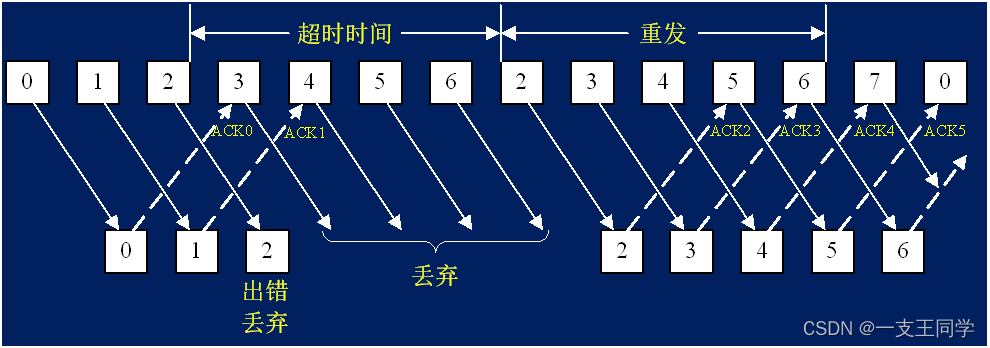
3.3 回退N帧的 ARQ 协议——例题
● 例1. 假设卫星信道的数据率为 1Mb/s,取卫星信道的单程传播时延为 250 ms,每一个数据帧长度是 1000 bit。忽略误码率、确认帧长和处理时间。试计算下列情况下的卫星信道可能达到的最大的信道利用率分别是多少?
(1) 停止-等待协议; (2) 连续 ARQ 协议,W T = 7 W_T = 7WT=7; (3) 连续ARQ协议,W T = 127 W_T = 127WT=127。
解:
(1) 发送时延:t S = 1000 b i t 1 M b / s = 1 m s t_S=\frac{1000\,bit}{1\,Mb/s}=1mstS=1Mb/s1000bit=1ms,信道利用率 η = t S t S + 2 t P = 1 m s 1 m s + 2 × 250 m s = 1 501 η=\frac{t_S}{t_S+2t_P}=\frac{1ms}{1ms+2\times 250ms}=\frac{1}{501}η=tS+2tPtS=1ms+2×250ms1ms=5011
(2) 发送时延:t S = 1000 b i t 1 M b / s = 1 m s t_S=\frac{1000\,bit}{1\,Mb/s}=1mstS=1Mb/s1000bit=1ms,信道利用率 η = W T × t S t S + 2 t P = 7 × 1 m s 1 m s + 2 × 250 m s = 7 501 η=\frac{W_T\times t_S}{t_S+2t_P}=\frac{7\times 1ms}{1ms+2\times 250ms}=\frac{7}{501}η=tS+2tPWT×tS=1ms+2×250ms7×1ms=5017
(3) 发送时延:t S = 1000 b i t 1 M b / s = 1 m s t_S=\frac{1000\,bit}{1\,Mb/s}=1mstS=1Mb/s1000bit=1ms,信道利用率 η = W T × t S t S + 2 t P = 127 × 1 m s 1 m s + 2 × 250 m s = 127 501 η=\frac{W_T\times t_S}{t_S+2t_P}=\frac{127\times 1ms}{1ms+2\times 250ms}=\frac{127}{501}η=tS+2tPWT×tS=1ms+2×250ms127×1ms=501127
● 例2. (2012年联考)两台主机之间的数据链路层采用了后退 N 帧协议(GBN)传输数据,数据的传输速率为 16 kbps,单向传播时延为 270 ms,数据帧的长度范围是 128~512 字节,接收方总是以数据帧等长的帧进行确认(即确认帧长度与发送的帧一样大)。为使信道利用率最高,帧序列的比特数至少是( )
A.5 B.4 C.3 D.2
解:
数据的传输速率 C = 16 k b / s C=16\,kb/sC=16kb/s
假设数据帧序列的比特数为 L LL,则数据帧的发送时延: t S = L / C , L ∈ [ 128 , 512 ] B y t e t_S=L/C,L∈[128,512]\,BytetS=L/C,L∈[128,512]Byte
因为确认帧长度与发送的帧一样大(和 L LL 一样大),且不能忽略 应答帧的发送时延 (和 t S t_StS 一样大)
传播时延: t P = 270 m s t_P=270\,mstP=270ms
我们知道,“帧序列的比特数 n nn” 和 “发送窗口的大小 W T W_TWT” 满足关系:W T ∈ [ 1 , 2 n − 1 ] W_T∈[1,2^{n}-1]WT∈[1,2n−1]
信道利用率:η = W T × t S 2 t S + 2 t P = 1 2 × W T × L / C L / C + t P = 1 2 × W T × L L + t P × C η=\frac{W_T\times t_S}{2t_S+2t_P}=\frac{1}{2}\times \frac{W_T \times L/C}{ L/C+t_P}=\frac{1}{2}\times \frac{W_T \times L}{L+t_P\times C}η=2tS+2tPWT×tS=21×L/C+tPWT×L/C=21×L+tP×CWT×L
现在是,我们需要考虑到最极端的情况,则即什么样的 “帧序号 n nn 的编码数” 能满足 “无论何时都能够使得信道利用率最高”。
我们对 信道利用率 做一点改动:η = 1 2 × W T × L L + t P × C = 1 2 × W T 1 + t P × C L η=\frac{1}{2}\times \frac{W_T \times L}{L+t_P\times C} = \frac{1}{2}\times \frac{W_T}{1+ \frac{t_P\times C}{L}}η=21×L+tP×CWT×L=21×1+LtP×CWT
从上述公式,不难看出,如果我们使得在分母最大的时候,都能使得信道利用率能达到最高,即可。
我们将 L = 128 × 8 b L=128\times8\,bL=128×8b 带入上述公式得:η = 1 2 × W T 1 + 270 m s × 16 k b / s 1024 b = W T 10.4375 η= \frac{1}{2}\times \frac{W_T}{1+ \frac{270\,ms\times 16\,kb/s}{1024\,b}} =\frac{W_T}{10.4375}η=21×1+1024b270ms×16kb/sWT=10.4375WT
我们应该知道,在理论上无论使用 128B 还是 512B 都可以使 信道利用率 达到最大的 100%。,只要 W T W_TWT 足够大。而这里我们要做的是,选择最小的 “帧序列的比特数 n nn ” 能够使得 信道利用率 达到最大,即 1 11。
故 η = 2 n − 1 10.4375 > = 1 , 解 得 : n > = 4 故 η= \frac{2^{n}-1}{10.4375}>=1,解得:n>=4故η=10.43752n−1>=1,解得:n>=4
所以答案选 B。
四、补充说明
● 因为本文重点针对的是 “信道利用率” 的计算。
● 所以弱化了对 “停止-等待协议” 和 “回退N帧的ARQ协议” 的定义的讲解。
● 另外,还有一种 “选择ARQ协议”,考试中大题考得较少,就没写,但是理论还是要掌握。
● 若有写得不对的地方,或有疑问,欢迎评论交流。
⭐️ ⭐️