选取了2000年1月至2020年5月的纳斯达克指数每个工作日的收盘价作为研究对象,绘制其时序图并作出初步分析。由原始序列时序图可以看出,该时间序列具有较强的趋势性。
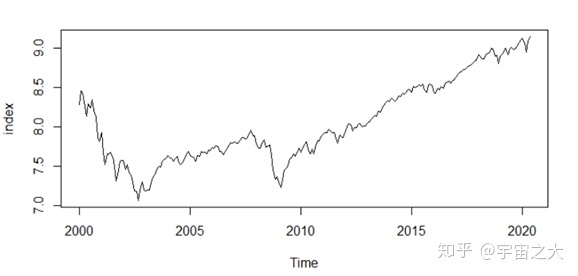
为确定其是否为白噪声,进行Box-test检验,检验结果显示P值小于0.05,显然原始序列不是白噪声。

为了拟合股票价格走势,拟合模型是重中之重,为比较不同模型的拟合效果,进行了不同模型的拟合对比分析,主要思路如下:
一、数据的录入,对原数据进行预处理;
二、利用非线性回归的方法进行建模;
三、利用Holt-winters三参数方法进行建模;
四、通过自相关图和ADF检验,检验处理后数据的平稳性,进行下一步ARIMA建模;
五、在同方差的假定下拟合ARIMA模型,根据AIC准则进行定阶;
六、对第五步中的残差进行检验是否存在异方差性,拟合ARCH-GARCH模型;
七、利用rugarch包对ARIMA(3,1,2)-GARCH(1,2)模型进行拟合和预测。
模型拟合
1.非线性回归模型
考虑到纳斯达克指数走势呈现出明显的非线性特点,故使用二次曲线进行拟合。结果显示,开盘价的二次项回归系数为7.198,一次项回归系数为-2.887,它的系数在p<0.01的水平下显著不为0。总的来说,自变量解释了收盘价86.69%方差。

利用二次曲线模型进行拟合并做出预测,并根据AIC准则进行模型拟合度的判定,为此,选择记录了每次AIC信息。最终拟合效果图如下:
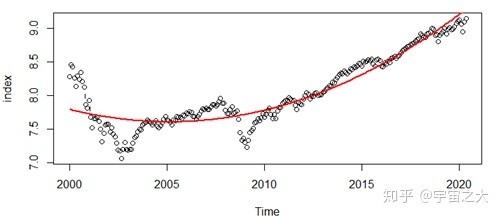
2.Holt-winters三参数模型
由代码实现可得出三次指数平滑算法的平滑参数α=0.7624061,β=0.03035442,γ=1,三次指数平滑可以很好的保存时间序列数据的趋势和季节性信息,根据其拟合图,可以看出其在股市收盘价数据集上效果很好。
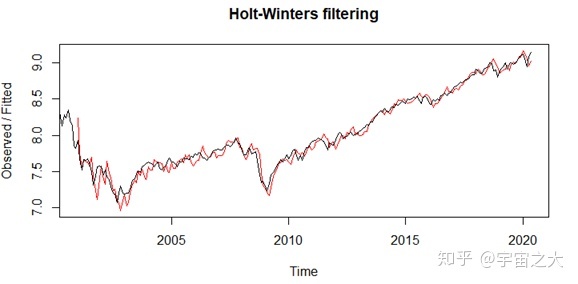
进一步做出6期预测,预测如下:
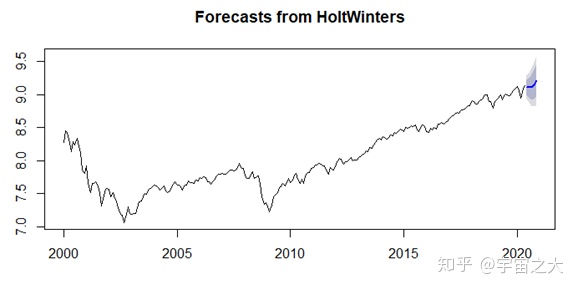
3.平稳性检验
对收盘价进行自相关分析。从图3-7中可以看出,自相关系数没有很快的趋近于0,可以初步判断序列是非纯随机、非平稳的。为进一步判断其平稳性,还对其进行了单位根检验,运行得出p值为0.8142,远远大于0.0.5,无法拒绝原假设,故序列不平稳。为进行下一步操作,需要将序列转化为平稳序列。
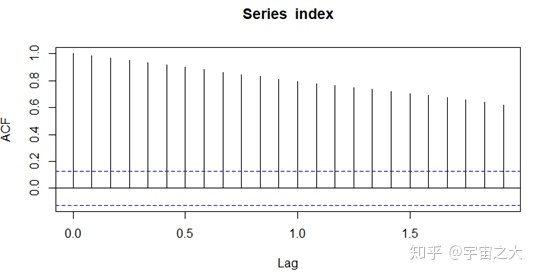
由于收盘价数值变化范围较大,对其取对数进行降维,再做一阶差分运算。绘制出一阶差分后序列的时序图和自相关图,可以发现序列的趋势性明显被剔除,序列基本平稳。对此进行单位根检验,从单位根检验p值明显小于0.05,故一阶差分后序列是平稳的。

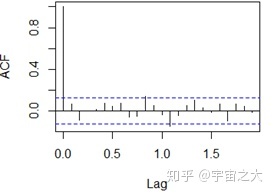
4.ARIMA模型
在差分运算后,趋势图和 ADF 检验结果都显示序列已经是平稳序列,故可以进行ARIMA模型的拟合。针对纳斯达克指数收盘价的差分序列,从s下图可以看出根据 ARMA 模型的AC和PAC图在q阶和p阶之后呈现出拖尾特征,其ARMA模型的p和q分别可以选择 1、2、3、4,并据AIC准则选择最小的,最终选择ARIMA(3,1,2)模型进行拟合。



ARIMA(3,1,2)模型拟合的参数结果如下图所示

对AIRMA(3,1,2)的残差序列进行白噪声检验,结果表明残差序列是白噪声的,说明ARIMA(3,1,2)模型信息提取充分。

为确定残差序列的趋势性,对其进行K-S检验,检验其是否服从正态分布,由代码运行结果可知:p-value<2.2e-16,拒绝原假设,故残差序列不服从正态分布。

为了提高模型拟合的精度,需要对残差序列进行方差齐性检验,并进行深入分析,对此绘制残差序列的时序图,可以看出残差序列在整个序列观察期,序列的方差基本是齐性的,但是在某几段时期内方差显著异于期望方差,故序列出现集群效应,残差序列存在异方差性。
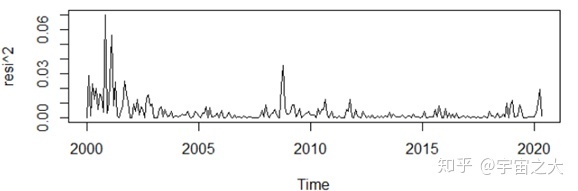
为进一步确定残差序列的异方差性,对残差序列进行LM检验和Portmanteau Q检验,由代码运行结果知两个检验结果均显示p值明显小于显著性水平0.05,故拒绝原假设,则可知,残差序列具有自相关性,而其自相关性导致了异方差性。
5.GARCH模型
由运行结果可知,残差序列的异方差函数并不是短期自相关,而是具有长期自相关性,为避免产生很高的移动平均数,故可采用GARCH模型进行拟合,它可以有效拟合具有长期记忆性的异方差函数。
为得出拟合效果较好的模型,对GARCH模型的参数进行多次取值拟合,根据AIC准则,应选去AIC值最小的模型,按不同模型的AIC数值从小到大排序,结果如下表1。故最终选用GARCH(1,2)模型进行拟合.

依GARCH(1,2)模型对ARIMA(3,1,2)残差序列进行预测,对条件异方差置信区间和方差齐性置信区间进行比较,可以看出异方差模型的拟合区间更符合实际。
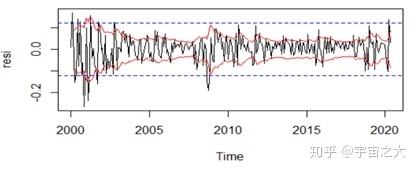
综上,根据AIC准则,得出不同模型的优劣,最终结果显示ARIMA (3,1,2)-GARCH(1,2)模型比较适合。

预测
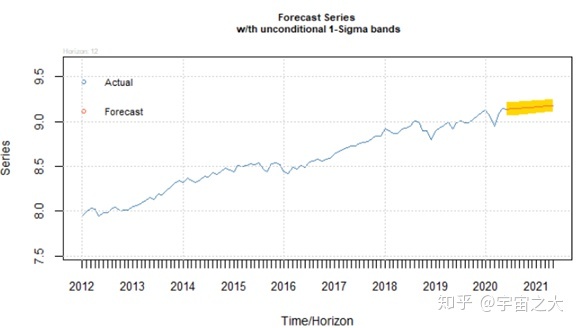
为了对ARIMA(3,1,2)-GARCH(1,2)模型进行预测,在R语言中调用“rugarch”包进行对应的模型拟合和预测,这里进行12期预测,预测值、预测图如下所示。

结论
通过对纳斯达克综合指数的时间序列拟合分析,可以看到纳斯达克综合指数受到国际经济形势的影响,分别在2000年,2008年,2020年出现异方差,主要原因分别是2000年的互联网经济泡沫,2008年金融危机以及2020年新冠疫情,同时可以通过模型预测未来纳斯达克综合指数会不断上升,得到修复。