前段时间刷树专题的时候 写了这篇文章 总结了遇到可以使用DFS思想 递归解题时的一个小套路
力扣树专题-4 用leetcode104求树的深度举例 总结递归秒杀树问题的套路! java刷题笔记
上次那道题可以应用 树问题中一个很常见的套路——求深度 来解决
本题亦是如此——110. 平衡二叉树
但是 不止如此——
在本次解题中 我对递归自底向上、自顶向下进行了更深刻的了解
并在优化我第一次写出来的丑陋冗余的代码的过程中更深入理解了递归的机制!
最终得到了很优美 很接近大佬的代码
来看看我的心路历程吧!!
如何写出优美的平衡二叉树判断代码
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
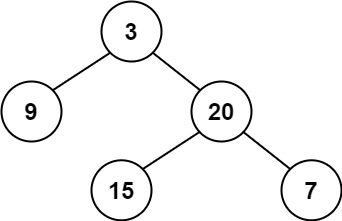
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
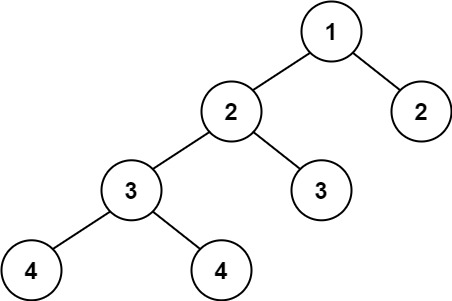
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
解题思路
我的解题思路(代码很丑陋!)
leetcode中发布的题解:Java自底向上的小白代码-套用求二叉树深度的模板 ~
用的“求二叉树的深度”的模板 中间掺杂了一个高度差的判断
思路还是来自之前自己总结的博客(递归解决求树深度的问题)
第一次尝到了套用模板的甜头 嘿嘿
下面来讨论下本文的重头戏!效率的优化!
自底向上的递归
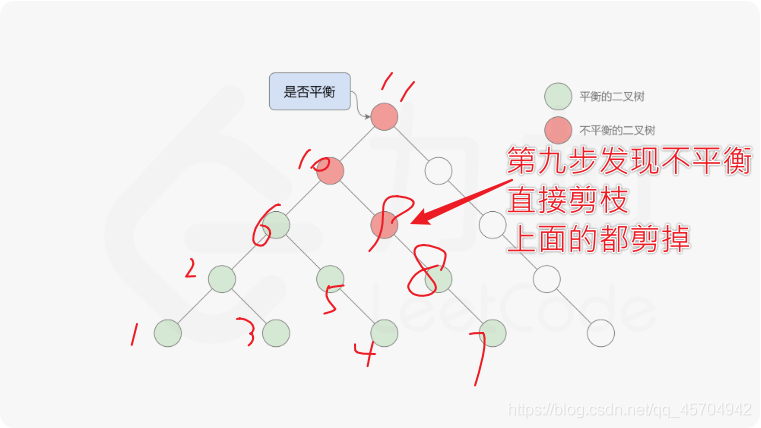
本题使用了自底向上的方法 注意这个方法是“提前阻断”的
也就是说 一旦碰到了不满足平衡二叉树的节点 就会进行“剪枝” (子节点剪掉的话 父节点同样剪掉)
时间复杂度为O(N) 只需要对节点进行一次“高度差的计算”就OK了!!
熟悉的剪枝hhh 之前数据挖掘课程中学习Apriori算法也有提到这个剪枝的作用——剪一个子类 父类都连坐~
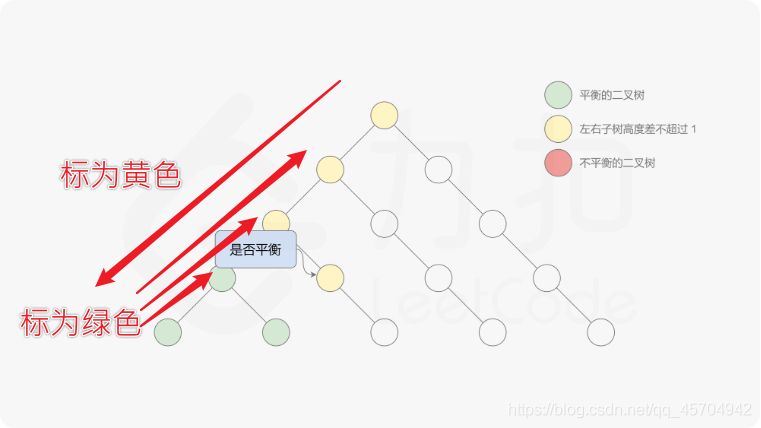
自顶向下的递归 效率会低很多!
时间复杂度为O(N2)
由于是自顶向下递归,因此对于同一个节点,函数height会被重复调用,导致时间复杂度较高
下面这个大哥说的还是有道理的
如果自顶向下递归(暴力解法)每走一步都要判断一下左右子树高度差 且回去的时候还要判断一遍
具体代码如下:class Solution { public boolean isBalanced(TreeNode root) { if (root == null) return true; return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);// } private int depth(TreeNode root) { if (root == null) return 0; return Math.max(depth(root.left), depth(root.right)) + 1; } }
Java代码
step1 根据之前总结的求二叉树深度的模板套出来的代码
这里就不得不提一句之前写那篇文章了
下面那里的思想是一样的嗷
虽然优美称不上 但是能解题就好!
class Solution {
boolean ans = true;
public boolean isBalanced(TreeNode root) {
dfs(root);
return ans;
}
//这里和求二叉树深度的部分的代码几乎一模一样的嗷
//在这段代码中 我们求得了ans 也就是这个二叉树的平衡二叉树与否
public int dfs(TreeNode root){
if(root == null){
return 0;
}
int ldepth = dfs(root.left);
int rdepth = dfs(root.right);
//01 自底向上求法 时间复杂度是O(N) 先抵达最底部 然后一点点向上更新深度
//每层深度 = Math.max(ldepth, rdepth) + 1 //只要没出现不平衡的情况 就更新深度嗷
if(Math.abs(ldepth - rdepth) > 1){
//02 一旦左右子树深度之差 > 1 就不是平衡二叉树了!
ans = false;
}
return Math.max(ldepth, rdepth) + 1
}
}
step2 优化后的简洁一些的代码
而且返回也不是傻傻的true和false了orz
class Solution {
public boolean isBalanced(TreeNode root) {
return depth(root) >= 0;
}
//这里和求二叉树深度的部分的代码几乎一模一样的嗷
//在这段代码中 我们求得了ans 也就是这个二叉树的平衡二叉树与否
public int depth(TreeNode root){
if(root == null){
return 0;
}
int ldepth = depth(root.left);
int rdepth = depth(root.right);
//01 自底向上的求法 时间复杂度是O(N) 先抵达最底部 然后一点点向上更新深度
if(ldepth == -1 || rdepth == -1 || Math.abs(ldepth - rdepth) > 1){
//02 一旦左子树或右子树有一个不满足的就直接向上返回return -1 不需要重复计算深度了
//02 一旦左右子树深度之差 > 1 就不是平衡二叉树了!
return -1;
}
return Math.max(ldepth, rdepth) + 1;
}
}
step3 代码优美程度的探究过程
写到这里产生了疑问
就是
这段存在的必要性
- 这里首先要理解递归
- 然后又问了一下大佬 得到解答——
豁然开朗!递归函数实际上是一个函数栈呐!
在“查字典”途中找到了某一层的单词 我们要返回给上一层(用于理解上一层字典的意思) 直到返回到栈顶(理解了最开始那句话的意思 查字典成功!)
上面的问题解决了
但是其实还可以再优化一下
step4 进一步优化!
因为 还是遍历了所有滴节点!
如果左子树已经发现不平衡了 还是会傻乎乎地递归一遍右子树!
int ldepth = depth(root.left); int rdepth = depth(root.right); //就因为这两行代码中使用了赋值语句 //已经调用了递归函数!那我不想遍历右边儿节点 咋整?
看下面嗷~ 把赋值语句放到语句中 利用语句的短路效应 来跳过右边节点的遍历就好了!
这里和下面K神的代码思路是一致的
在进行递归之前 先判断下我这个左子树是不是已经不平衡了
如果不平衡 -1 再走几步向上传到栈顶的位置 得到结果false(后面的right子树压根不用遍历了!)
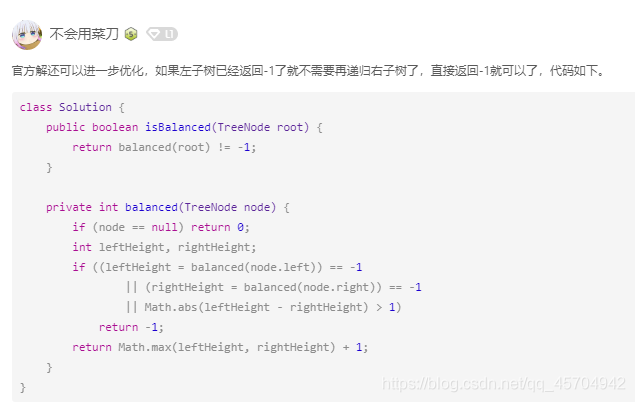
step5 (读)K神简洁的代码
这段写的是真好啊!就记住这个就完事了!
class Solution {
public boolean isBalanced(TreeNode root) {
return recur(root) != -1;
}
private int recur(TreeNode root) {
if (root == null) return 0;
int left = recur(root.left);
if(left == -1) return -1;
int right = recur(root.right);
if(right == -1) return -1;//现在一看 这段代码才是在第五层啊!
//每一步都有一个清清楚楚的判断 避免“左子树发现不平衡 还依旧遍历右子树”
return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
}
}
final step!参考大佬们思路后的最优代码(代码变得优美了!)
终于是得到了本题的最优解(应该是吧哈哈哈)
class Solution {
public boolean isBalanced(TreeNode root) {
return depth(root) != -1;
}
public int depth(TreeNode root){
if(root == null){
return 0;
}
// 左子树如果遇到不平衡情况后面可以不考虑高度差的问题 直接向上返回-1
int ldepth = depth(root.left);//另外 如果左边递归到栈顶的过程中出现了不平衡情况
if(ldepth == -1) return -1;//到栈顶时 depth(root)直接返回-1
int rdepth = depth(root.right);//右子树如果遇到不平衡情况后面可以不考虑高度差的问题 直接向上返回-1
if(rdepth == -1) return -1;
// if(Math.abs(ldepth - rdepth) > 1) return -1;
// else{
// return Math.max(ldepth, rdepth) + 1;
// } 再优化下 用三元表达式写return哈哈哈(像dl一样写代码orz)
return Math.abs(ldepth - rdepth) > 1 ? -1 : Math.max(ldepth, rdepth) + 1;
}
}
附上写本题以及改进过程中我的心路历程orz