POJ 2488-A Knight's Journey

题目链接：http://poj.org/problem?id=2488

A Knight’s Journey

Background
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
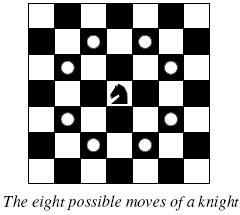
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?

Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, … , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, …

Output

The output for every scenario begins with a line containing “Scenario #i:”, where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
Sample Input

3
1 1
2 3
4 3`

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

题目大意：有一个骚年没事干，就想着把一个矩形的棋盘以马走日的形式走完，问他能把这个棋盘按字典序走完最先走的是哪条路径？输入要测试的棋盘数和棋盘的。如果走不完输出”impossible“,能走完输出走的路径，行按字符输出，列按数字输出。
解题思路：
一个深搜问题首先考虑中间的状态。很容易想到中间的状态就是在走完n步后，当前的行和列值。然后确定初始状态和终止状态。在这里，起始状态就是走第0行0列的格子，终止状态就是把所以得格子走完，也就是走了p*q个格子。然后考虑的就是状态的变化，在这里就是从当前的(r,c)->(r+X[i],c+Y[i])。再判断下有没有出棋盘，前面有没有走过，最后就是单纯的递归了。
注意问题：
(1)以马走日的形式，走过的格子是当前格子和最后到达的格子，中间路过的格子不计在内。楼主也是够了，刚开始的时候居然把中间的格子算上了，结果半天不知道中间格子怎么标记，也是够了。
(2)输入的先是列数后是行数，不注意的话，真的都不知道哪出问题了。
(3)以字典序去搜周围符合条件的点，这个字典序我还真不知道怎么弄，看了各路大神的程序，总算明白了。
代码片：

```
#include<iostream>
#include<string.h>
#include<cstdio>
using namespace std;

const int SIZE = 26;
const int  X[8] = { -2, -2, -1, -1, 1, 1, 2, 2 };
const int Y[8] = { -1, 1, -2, 2, -2, 2, -1, 1 };//字典序的行列值
int StepX[SIZE], StepY[SIZE];//记录走的路径
int Chess[SIZE][SIZE];  //棋盘
int total, row, column, step, Sign;

void DFS(int r, int c)
{
    int x, y;
    if (Sign == 1)//跟大牛学的终止条件的写法
    {
        return;
    }
    step++;
    StepX[step] = r;
    StepY[step] = c;
    if (step == row*column)//终止条件
    {
        Sign = 1;
        return;
    }
    Chess[r][c] = 1;//走过标记
    for (int i = 0; i < 8; i++)
    {
        y = c + Y[i];
        x = r + X[i];//按字典序去搜
        if (x <= row && y <= column&&x>0 && y > 0 && Chess[x][y] == 0)
        {
            DFS(x, y);//递归
            step--;
        }
    }
    Chess[r][c] = 0;//当前行列找不到合适的走法回溯
}
int main()
{
    int k, t = 1;
    cin >> k;
    while (k--)
    {
        step = 0;
        Sign = 0;
        memset(Chess, 0, sizeof(Chess));
        memset(StepX, 0, sizeof(StepX));
        memset(StepY, 0, sizeof(StepY));
        cin >> column >> row;
        cout << "Scenario #" << t++ << ":" << endl;
        DFS(1, 1);
        if (Sign)
        {
            for (int i = 1; i < row*column + 1; i++)
                cout << char(StepX[i] - 1 + 'A') << StepY[i];
            cout << endl;
        }
        else cout << "impossible" << endl;
        if (k != 0)
        {
            cout << endl;
        }

    }
    return 0;
}