s-palindrome
题面翻译
给出一个字符串,判断这个字符串中间是否是对称的。
是输出“TAK”,不是输出“NIE”。
@[chen_zhe](/space/show?uid=8457) @[yjjr](/space/show?uid=5088)
题目描述
Let’s call a string “s-palindrome” if it is symmetric about the middle of the string.
For example, the string “oHo” is “s-palindrome”, but the string “aa” is not.
The string “aa” is not “s-palindrome”, because the second half of it is not a mirror reflection of the first half.
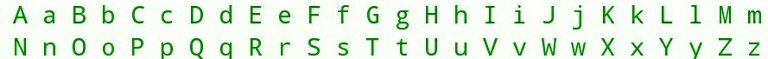 English alphabetYou are given a string s ss .
English alphabetYou are given a string s ss .
Check if the string is “s-palindrome”.
输入格式
The only line contains the string s ss ( 1 < = ∣ s ∣ < = 1000 1<=|s|<=10001<=∣s∣<=1000 ) which consists of only English letters.
输出格式
Print “TAK” if the string s ss is “s-palindrome” and “NIE” otherwise.
样例 #1
样例输入 #1
oXoxoXo
样例输出 #1
TAK
样例 #2
样例输入 #2
bod
样例输出 #2
TAK
样例 #3
样例输入 #3
ER
样例输出 #3
NIE
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
char s[1100];
char f[255];
int l;
int main(){
f['A']='A';f['H']='H';f['I']='I';f['M']='M';f['O']='O';f['T']='T';
f['U']='U';f['V']='V';f['W']='W';f['X']='X';f['Y']='Y';f['b']='d';
f['d']='b';f['o']='o';f['p']='q';f['q']='p';f['v']='v';f['w']='w';
f['x']='x';
scanf("%s",s);
l=strlen(s);
for(int i=0,j=l-1;i<=j;++i,--j){
if(f[s[i]]!=s[j]){
puts("NIE");return 0;
}
}
puts("TAK");
return 0;
}
Memory and De-Evolution
题面翻译
Memory对物体,尤其是三角形的变化感兴趣。 他有一个边长为x的等边三角形,他希望通过一些操作获得一个边长为y的等边三角形。
他一次可以修改当前三角形一边的长度,修改后也应为合法的三角形。
每次修改后,每一边的长度都应该是整数。
Memory要获得边长y的等边三角形,所需的最小修改次数是多少?
输入格式:
第一行包含两个整数x和y(3<=x<y<=100000),分别为最开始的三角形边长与想要获得的三角形边长。
输出格式:
输出一个整数,即为最小的修改次数。
题目描述
Memory is now interested in the de-evolution of objects, specifically triangles.
He starts with an equilateral triangle of side length x xx , and he wishes to perform operations to obtain an equilateral triangle of side length y yy .
In a single second, he can modify the length of a single side of the current triangle such that it remains a non-degenerate triangle (triangle of positive area).
At any moment of time, the length of each side should be integer.
What is the minimum number of seconds required for Memory to obtain the equilateral triangle of side length y yy ?
输入格式
The first and only line contains two integers x xx and y yy ( KaTeX parse error: Expected 'EOF', got '&' at position 5: 3<=y&̲lt;x<=100000 ) — the starting and ending equilateral triangle side lengths respectively.
输出格式
Print a single integer — the minimum number of seconds required for Memory to obtain the equilateral triangle of side length y yy if he starts with the equilateral triangle of side length x xx .
样例 #1
样例输入 #1
6 3
样例输出 #1
4
样例 #2
样例输入 #2
8 5
样例输出 #2
3
样例 #3
样例输入 #3
22 4
样例输出 #3
6
提示
In the first sample test, Memory starts with an equilateral triangle of side length 6 66 and wants one of side length 3 33 .
Denote a triangle with sides a aa , b bb , and c cc as ( a , b , c ) (a,b,c)(a,b,c) .
Then, Memory can do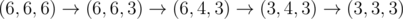 .
.
In the second sample test, Memory can do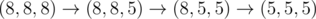 .
.
In the third sample test, Memory can do:
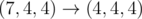 .
.
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
int x,y,a[4],k=0;
int main(){
cin>>x>>y;
a[1]=a[2]=a[3]=y;
while(a[1]<x||a[2]<x||a[3]<x){
k++;
sort(a+1,a+4);
a[1]=a[2]+a[3]-1;
}
cout<<k<<endl;
return 0;
}
The Same Calendar
题面翻译
给你一个年份n,给出一个大于n的年份,有如下两个要求
1.天数与n相同
2.该年的第一天的星期与n年相同
闰年有366天。整除4且不整除100的是闰年,整除400的也是闰年
题目描述
The girl Taylor has a beautiful calendar for the year y yy .
In the calendar all days are given with their days of week: Monday, Tuesday, Wednesday, Thursday, Friday, Saturday and Sunday.
The calendar is so beautiful that she wants to know what is the next year after y yy when the calendar will be exactly the same.
Help Taylor to find that year.
Note that leap years has 366 366366 days. The year is leap if it is divisible by 400 400400 or it is divisible by 4 44 , but not by 100 100100 (https://en.wikipedia.org/wiki/Leap_year).
输入格式
The only line contains integer y yy ( KaTeX parse error: Expected 'EOF', got '&' at position 8: 1000<=y&̲lt;100'000 ) — the year of the calendar.
输出格式
Print the only integer y ′ y'y′ — the next year after y yy when the calendar will be the same.
Note that you should find the first year after y yy with the same calendar.
样例 #1
样例输入 #1
2016
样例输出 #1
2044
样例 #2
样例输入 #2
2000
样例输出 #2
2028
样例 #3
样例输入 #3
50501
样例输出 #3
50507
提示
Today is Monday, the 13 1313 th of June, 2016 20162016 .
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
int n,m,k;
bool check(int x){
if((x%4==0&&x%100!=0)||x%400==0)return 1;
return 0;
}
int main(){
cin>>n;
m=n;
do{
++m;
k=(k+365+check(m))%7;
}while(!(check(n)==check(m)&&k==0));
cout<<m<<endl;
return 0;
}
Tennis Championship
题面翻译
有一个n nn 个节点的二叉树。
要求每个节点的两个儿子的子树最大深度相差不超1 11,求最大深度。
n < = 1 0 18 n <= 10^{18}n<=1018
感谢@Harryheqg 提供的翻译
题目描述
Famous Brazil city Rio de Janeiro holds a tennis tournament and Ostap Bender doesn’t want to miss this event.
There will be n nn players participating, and the tournament will follow knockout rules from the very first game.
That means, that if someone loses a game he leaves the tournament immediately.
Organizers are still arranging tournament grid (i.e. the order games will happen and who is going to play with whom) but they have already fixed one rule: two players can play against each other only if the number of games one of them has already played differs by no more than one from the number of games the other one has already played.
Of course, both players had to win all their games in order to continue participating in the tournament.
Tournament hasn’t started yet so the audience is a bit bored.
Ostap decided to find out what is the maximum number of games the winner of the tournament can take part in (assuming the rule above is used).
However, it is unlikely he can deal with this problem without your help.
输入格式
The only line of the input contains a single integer n nn ( 2 < = n < = 1 0 18 2<=n<=10^{18}2<=n<=1018 ) — the number of players to participate in the tournament.
输出格式
Print the maximum number of games in which the winner of the tournament can take part.
样例 #1
样例输入 #1
2
样例输出 #1
1
样例 #2
样例输入 #2
3
样例输出 #2
2
样例 #3
样例输入 #3
4
样例输出 #3
2
样例 #4
样例输入 #4
10
样例输出 #4
4
提示
In all samples we consider that player number 1 11 is the winner.
In the first sample, there would be only one game so the answer is 1 11 .
In the second sample, player 1 11 can consequently beat players 2 22 and 3 33 .
In the third sample, player 1 11 can’t play with each other player as after he plays with players 2 22 and 3 33 he can’t play against player 4 44 , as he has 0 00 games played, while player 1 11 already played 2 22 .
Thus, the answer is 2 22 and to achieve we make pairs ( 1 , 2 ) (1,2)(1,2) and ( 3 , 4 ) (3,4)(3,4) and then clash the winners.
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
ll n,s1=1,s2=2,s3=3,k=1;
int main(){
cin>>n;
while(s3<=n){
s1=s2;
s2=s3;
s3=s1+s2;
k++;
}
cout<<k<<endl;
return 0;
}
Buses Between Cities
题面翻译
题目大意
A AA市和B BB市之间有公交车行驶,第一班是早上5 : 00 5:005:00,最后一班不迟于晚上11 : 59 11:5911:59开出。
从A AA市出发的公共汽车每隔a aa分钟发车,到B BB市需t a t_ata分钟,从B BB市出发的公共汽车每隔b bb分钟发一辆车,到A AA市需t b t_btb分钟。
司机S i m o n SimonSimon吃饱了没事干增加工作的乐趣,数了数在他的行程途中向他驶来的公交车,但S i m o n SimonSimon没有计算他在起点和终点遇到的公共汽车。
给定S i m o n SimonSimon从A AA城到B BB城的时间,计算Simon将会见到的公共汽车的数量。
输入格式
第一行:两个整数a aa与t a t_ata( 1 ≤ a , t a ≤ 120 ) (1\le a,t_a\le 120)(1≤a,ta≤120)。
第二行:两个整数b bb与t b t_btb( 1 ≤ b , t b ≤ 120 ) (1\le b,t_b\le 120)(1≤b,tb≤120)。
ps:a , t a , b , t b a,t_a,b,t_ba,ta,b,tb单位均为分钟。
第三行:S i m o n SimonSimon从A AA市出发的时间,格式:h h : m m hh:mmhh:mm(h为小时,m为分钟,且两者均用两位数表示)。
ps:S i m o n SimonSimon从A AA市出发时一定有一辆公交车从A AA市开出。
输出格式
一个整数z zz,表示S i m o n SimonSimon在路上遇到的公交车的数量。
( t r a n s l a t e d (translated(translated b y byby D r e a m i n g B o y W o n d e r s ) DreamingBoyWonders)DreamingBoyWonders)
题目描述
Buses run between the cities A AA and B BB , the first one is at 05:00 AM and the last one departs not later than at 11:59 PM.
A bus from the city A AA departs every a aa minutes and arrives to the city B BB in a t a t_{a}ta minutes, and a bus from the city B BB departs every b bb minutes and arrives to the city A AA in a t b t_{b}tb minutes.
The driver Simion wants to make his job diverse, so he counts the buses going towards him.
Simion doesn’t count the buses he meet at the start and finish.
You know the time when Simion departed from the city A AA to the city B BB .
Calculate the number of buses Simion will meet to be sure in his counting.
输入格式
The first line contains two integers a , t a a,t_{a}a,ta ( 1 < = a , t a < = 120 1<=a,t_{a}<=1201<=a,ta<=120 ) — the frequency of the buses from the city A AA to the city B BB and the travel time.
Both values are given in minutes.
The second line contains two integers b , t b b,t_{b}b,tb ( 1 < = b , t b < = 120 1<=b,t_{b}<=1201<=b,tb<=120 ) — the frequency of the buses from the city B BB to the city A AA and the travel time.
Both values are given in minutes.
The last line contains the departure time of Simion from the city A AA in the format hh:mm.
It is guaranteed that there are a bus from the city A AA at that time.
Note that the hours and the minutes are given with exactly two digits.
输出格式
Print the only integer z zz — the number of buses Simion will meet on the way.
Note that you should not count the encounters in cities A AA and B BB .
样例 #1
样例输入 #1
10 30
10 35
05:20
样例输出 #1
5
样例 #2
样例输入 #2
60 120
24 100
13:00
样例输出 #2
9
提示
In the first example Simion departs form the city A AA at 05:20 AM and arrives to the city B BB at 05:50 AM. He will meet the first 5 55 buses from the city B BB that departed in the period [05:00 AM - 05:40 AM].
Also Simion will meet a bus in the city B BB at 05:50 AM, but he will not count it.
Also note that the first encounter will be between 05:26 AM and 05:27 AM (if we suggest that the buses are go with the sustained speed).
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
int a,b,ta,tb,h,m;
int main(){
scanf("%d%d%d%d%d:%d",&a,&ta,&b,&tb,&h,&m);
m+=h*60;
h=0;
a=300;
while(a<m+ta&&a<1440){
if(a+tb>m) h++;
a+=b;
}
cout<<h<<endl;
return 0;
}