2021SC@SDUSC
本篇博客讲述一些关于模块反演的内容，参考Daniel J.Bernstein和Bo Yin Yang的论文“快速恒定时间gcd计算和模块反演”
目录
快速恒定时间gcd计算和模块反演
使用除法步骤计算最大公约数（GCD）
它计算奇数整数f和任意整数g的最大公约数。它的内部循环不断重写变量f和g以及状态变量&delta；从1开始，直到达到g=0。在这一点上，f给出了GCD。循环中的每个转换称为“分割步骤”（在下文中称为divstep）。
例如，gcd（21，14）的计算公式为：
-起始状态&delta=1 f=21 g=14
-以第三个分支&delta=2 f=21 g=7
-以第一个分支为例：&delta=-1 f=7 g=-7
-以第二个分支&delta=0 f=7 g=0
-答案| f |=7。
工作原理：
Divsteps可以分解为两个步骤
（a） 如果g是奇数，用（g，g-f）或（f，g+f）替换（f，g），得到偶数g。
（b） 将（f，g）替换为（f，g/2）（其中g保证为偶数）。
这两项操作都不会改变GCD：
对于（a），假设gcd（f，g）=c，那么f=a&thinsp；c和g=b&thinsp；c表示一些整数a和b。当（g，g-f）=（b&thinsp；c，（b-a）c）和（f，f+g）=（a&thinsp；c，（a+b）c）时，结果显然仍然有公因子c。另一方面的推理表明，这样做也不能增加任何共同因素。
对于（b），我们知道f是奇数，所以gcd（f，g）显然没有因子2，我们可以从g中去掉它。
该算法最终将收敛到g=0。由此我们最终找到了一个最终值f’，其gcd（f，G）=gcd（f’，0）。作为f’和0的gcd定义为
| f’|，这就是我们的答案。
&delta参数对于引导算法缩小数字的大小是必要的，而无需明确查看高阶位。
以后将变得重要的属性：
执行超过需要的步骤不是问题，因为在g=0之后f不再改变。
只有偶数被2除。这意味着，当用代数方法进行推理时，我们不需要担心舍入问题。
在算法执行过程中的每一点上，接下来的N个步骤仅取决于f和g的底部N位以及&delta。
以下使用python实现的代码部分：
从GCDs到模逆
我们需要一个算法来计算模M的x的逆a，即a的个数，使得a&thinsp；x=1 mod M。仅当x和M的GCD为1时，此逆函数才存在，但当M为素数且0<x<M时，情况总是如此，假设存在模逆。结果表明，通过跟踪内部变量如何在每一步写入输入的线性组合，可以计算出该逆作为计算GCD的副作用（参见[扩展欧几里德算法]）
由于GCD为1，这样的算法将计算数字a和b，使得a&thinsp；x+b&thinsp；M=1。取该表达式mod M表示&thinsp；x mod M=1，我们看到a是x mod M的模逆。
如果模M为奇数，则可使用上述基于分步的GCD算法计算模逆。为此，计算gcd（f=M，g=x），同时跟踪额外的变量d和e，每个步骤d=f/x（mod M）和e=g/x（mod M）。
这里的f/x表示与x相乘得到f模M的数字，因为f和g被初始化为M和x分别，d和e刚开始是0（M/x modm=0/x modm=0）和1（x/xmodm=1）。
还请注意，在整个计算过程中跟踪d和e以确定反演的方法与本文不同。这里确定了整个计算的转移矩阵，并由此计算出逆矩阵。这里的方法避免了各种大小的2x2矩阵乘法的需要，并且在我们能够在C中进行的优化级别上似乎更快。
实现代码：
分批处理
每一步都可以表示为矩阵乘法，将转移矩阵（1/2t）应用于向量[f，g]和[d，e]
t = [ u, v ]
[ q, r ]
[ out_f ] = (1/2 * t) * [ in_f ]
[ out_g ] = [ in_g ]
[ out_d ] = (1/2 * t) * [ in_d ] (mod M)
[ out_e ] [ in_e ]
其中（u，v，q，r）是（0，2，-1，1），（2，0，1，1）或（2，0，0，1），取决于采用哪个分支。如上所述，结果f和g始终是整数。执行多个除法步骤对应于与所有结果的乘积相乘。单个步骤的转移矩阵。由于每个转移矩阵由整数除以2组成，这些矩阵的乘积将由整数除以2^N组成。更新d和e时，这些分割代价很高，因此我们延迟它们：我们计算按2 ^N缩放的组合转移矩阵的整系数，并且最后一步，按2N进行一次除法：
实现代码：
由于divstep中的分支完全由f和g的底部N位决定，因此计算转移矩阵的函数只需要查看这些底部位。此外，所有中间结果和输出都符合（N+1）位数字（f和g为无符号；u、v为有符号，q、 和r）这意味着使用64位整数可以设置N=62，一次计算62步的完整转移矩阵，而不需要任何大整数运算。这就是该算法高效的原因：它只需要每N步更新一次完整大小的f、g、d和e数。我们仍然需要函数来计算：
[ out_f ] = (1/2^N * [ u, v ]) * [ in_f ]
[ out_g ] ( [ q, r ]) [ in_g ]
[ out_d ] = (1/2^N * [ u, v ]) * [ in_d ] (mod M)
[ out_e ] ( [ q, r ]) [ in_e ]
因为divsteps变换只将偶数除以2，所以t&thinsp；[f，g]总是相等的。当t是N个divsteps的组合时，由此得出的f和g将是2^N的倍数，被2N除就是简单地将它们下移：
实现代码：
对于d和e，情况并非如此，我们需要一个“div2”函数的等价物来除以2^N mod M。如果我们预先计算了1/M mod 2 ^ N（它总是存在于奇数M中）
代码实现
有了所有这些，我们可以编写一个版本的’modinv’，一次执行N个步骤：
这意味着在实践中，我们将始终执行N个步骤的倍数。这不是问题，因为一旦g=0，进一步的除法步骤就不再影响f、g、d或e（只有&delta不断增加）。对于可变时间代码，这些多余的迭代将在后面的章节中进行优化。
避免模运算
到目前为止，我们在两个地方计算模M的大数的余数：在每个“update_de”中的“div2n”的末尾，以及在“modinv”的最末尾，由于f的符号可能会对d求反。一般来说，这些操作都是相对昂贵的。要处理’div2n’中的模运算，我们只需停止要求d和e始终在[0，M）范围内。让我们从将’div2n’内联到’update_de’开始，并删除模最后的操作：
让我们看看这些数字范围的界限。可以证明| u |+| v |和| q |+| r |永远不会超过2N，因此与t相乘的输出的绝对值最多是最大绝对输入值的2N倍。如果输入d和e在（-M，M）中，这对于初始值d=0和e=1（假设M>1）来说肯定是正确的，乘法的结果是范围内的数字减去小于2N乘以M以抵消N位，使之达到（-2^ N+1^ M，2 ^ N^M），最后除以2N即为（-2M，M）“update_de”的另一个应用程序将采用这种方式.到（-3M，2M），以此类推。变量范围的逐步扩展可以通过在变量为负值时将d和e增加M来抵消：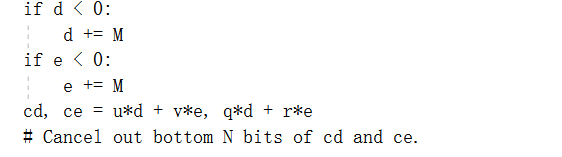
当输入为（-2M，M）时，它们将首先被移入范围（-M，M），这意味着输出将再次为（-2M，M），无论有多少次“update_de”调用，情况仍然如此。在下面的内容中，我们将尝试使其更有效；q&thinsp的M和ce；M.同样地，将e增加M等于将cd增加v&thinsp；r&thinsp的M和ce；M.所以我们可以写：
现在请注意，我们有两个步骤对cd和ce进行修正，它们将M的倍数相加：这个增量，和抵消底部位的减量。第二个取决于第一个，但它们仍然可以通过只计算cd和ce的底部位来有效组合。首先，使用它们来计算最终的md，me值：
最后一个优化：我们可以避免md&thinsp；M和我&thinsp；在cd的底部位进行M次乘法和ce，将其移动到md和me校正：
结果函数将（-2M，M）范围内的d和e作为输入，并输出相同范围内的值。这也意味着’modinv’末尾的d值将在该范围内，而我们希望得到[0，M]中的结果。为此，我们需要一个规范化函数。很容易将d的条件求反（基于f的符号）也集成到其中：
定时操作
该算法的主要卖点是快速恒定时间运算。还有什么代码流取决于目前为止的输入数据？
-while g&ne的迭代次数
-modinv’中的0循环
-divsteps_n_matrix的分支
-该标志签入update_de
-该符号签入“normalize”`
要使“modinv”中的while循环保持恒定时间，可以将其替换为恒定数量的迭代。
为了处理’divsteps\u n_matrix’中的分支，我们将用常量时间按位替换它们操作（希望C编译器不够聪明，无法将它们转换回分支；请参阅valgrind_ctime_test.c用于自动测试，但事实并非如此）。
代码实现：
为了将上述操作转换为按位操作，我们依赖一个条件求反的技巧：根据2的补码中负数的定义，（-v==~v+1）对每个数字v都有效。由于2的补码中的-1都是1位，所以位翻转可以用-1表示为异或。因此-v==（v^ -1）-（1）。因此，如果我们有一个值为0或-1的变量c，那么（v^c）-c在c=0时为v，在c=-1时为-v。
以恒定时间形式，如下所示：
为了使用这个技巧，我们需要一个助手掩码变量c1来解析条件&delta>0到-1（如果为真）或0（如果为假）。我们使用右移计算c1，这相当于除以指定的2的幂并向下舍入。因此，右移63将[-2^ 63,0）范围内的所有数字映射为-1，将[0,2^63）范围内的数字映射为0。利用x&0=0和x&（-1）=x的事实（再次在两个补码系统上），我们可以写出：
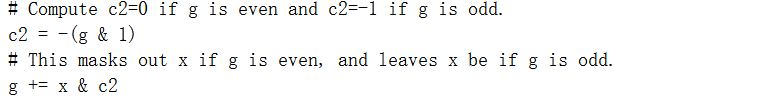
再次使用条件否定技巧，我们可以写：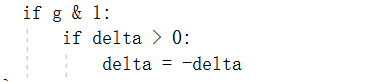
最终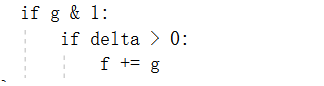
事实证明，通过应用替换&eta=-&希腊字母表的第4个字母在这种表述中，否定&delta；对应于否定&eta；，和增量&delta；对应于递减&eta；。这允许我们在c1计算中删除否定：
可以使用最坏情况下性能更好的divsteps变体：starting&delta；1/2而不是1。这将256位输入的最坏情况迭代次数减少到590次（可使用凸包分析显示）。在这种情况下，替换&zeta=-（&delta；+1/2）用于保持变量为整数。增量&增量；到1仍然转化为递减&zeta；由1，但否定&delta；现在对应于从&zeta；到-（&zeta；+1）或~&zeta；。基于c3有条件地这样做很简单：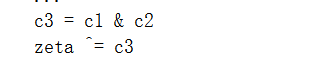
通过将“divsteps\u n_矩阵”中的循环替换为上述divstep代码的一个变体（扩展为也将所有f运算应用于u、v，将所有g运算应用于q、r），获得了“divsteps\u n_矩阵”的恒定时间版本。完整的代码将在第7节中介绍。这些位篡改技巧也可用于在update_de和’normalize`恒定时间。
可变时间优化
构建一个更快的非恒定时间’divsteps\n\u matrix’函数。
要做到这一点，首先要考虑编写DIVIDEA操作的内部循环的另一种方法。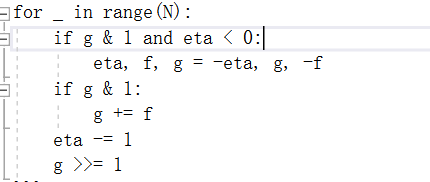
每当g为偶数时，循环仅向下移动g并减小&eta；。当g以多个零位结束时，这些迭代可以合并为一个步骤。这需要有效地计算底部零位，这在大多数平台上都是可能的；它在这里被抽象为函数“count\u training\u zeros”。
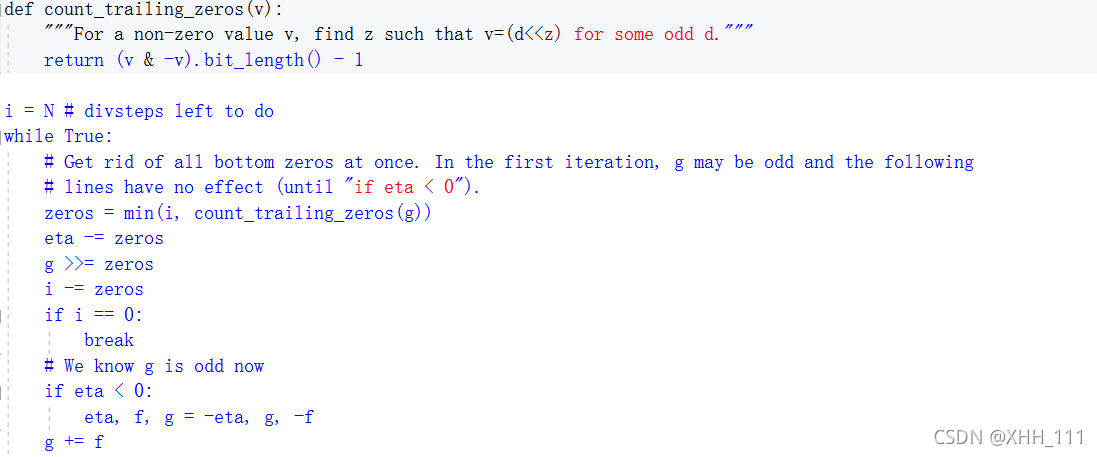现在我们可以一次从g中删除多个底部0位，但只要有底部1位，就仍然需要一次完整的迭代。在下面的内容中，我们还将同时删除多个1位。
请注意，只要&eta&geq；0时，循环不会修改f。相反，它取消了的底部位并将其移出，并减少&eta；因此，我只在&eta；变为负值，或者当我达到0时。结合起来，这相当于将f和g的倍数相加以抵消多个底部位，然后将它们移出。
很容易找到这个倍数是什么：我们想要一个数字w，这样g+w&thinsp；f有几个底部零位。如果这个位数是L，我们需要g+w&thinsp；f mod 2^L=0，或w=-g/f mod 2^L。由于f是奇数，任何L都存在这样的w。L不能超过i步（正如我们之前完成的循环）或超过&eta+1个步骤（正如我们在那一点上运行’eta，f，g=-eta，g，f’），但除此之外，我们只受到计算复杂性的限制。
此代码演示如何取消每个步骤最多4位：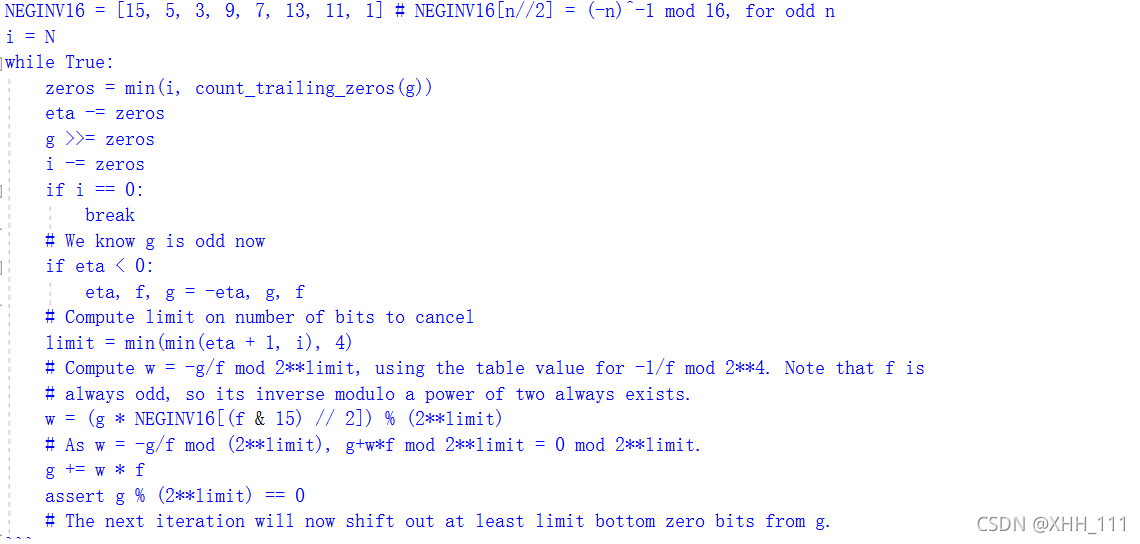
通过使用更大的表，可以一次取消更多的位。该表也可以实现作为一个公式。已知计算两个的模幂的模逆的几个公式；
这里我们需要求反模逆，它是这些的简单变换：
代替3位表：-f或f^6
代替4位表：1-f（f+1）
对于较大的表格，可以使用以下技术：
如果w=-1/f模2^L，则w（w&thinsp；f+2）为
-1/f模块2 ^ 2。这允许扩展以前的公式（或表格）。特别是我们有这个6位函数（基于上面的3位函数）：f（f^2-2）这个循环，再次扩展到处理u、v、q和r以及f和g，放在“divsteps\u n\u matrix”中，给出了一个更快但非恒定时间的版本。
最终版本：
一种在恒定时间内计算转移矩阵的方法，使用“divsteps\u n_matrix”函数，但其循环替换为恒定时间divstep的变体，扩展为处理u、v、q、r：
要获得可变时间版本，请将’divsteps_n_matrix’函数替换为divsteps循环的函数，以及在不使用固定迭代计数的情况下调用该函数的’modinv’版本：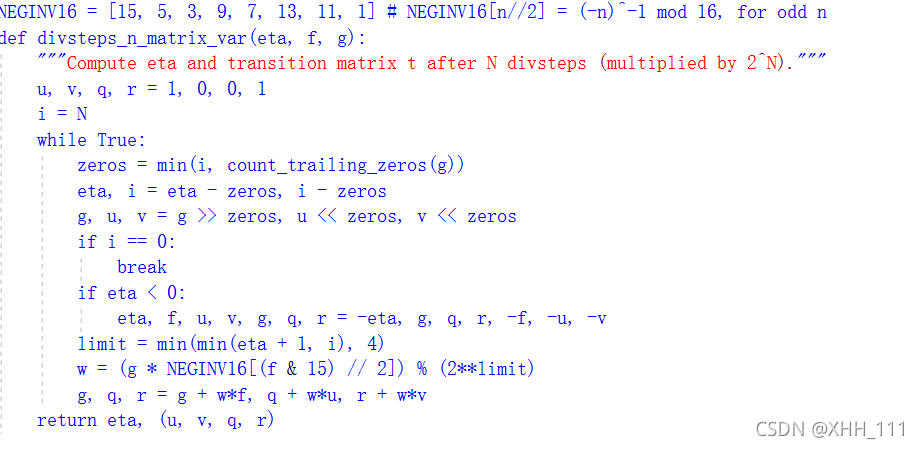
libsecp256k1中的代码实现
将x替换为其模逆mod modinfo->module。x必须在[0，模数]范围内。如果x为零，结果也将为零。如果不是，则必须存在倒数（即x和模数的gcd必须为1）。如果模数为素数，则自动满足这些规则。输出时，x的所有肢体都将在[0，2^30]范围内
取范围（-2模，模）内有符号的30号作为输入，并将模的倍数添加到范围[0，模）。如果符号<0，输入也将在过程中被求反。
在第一步中，如果输入为负，则添加模数，如果请求，则取反。这将使r从范围（-2模数，模数）变为范围（-模数，模数）。由于所有输入分支都在范围（-2^ 30,2^30）内，因此不能使int32\t溢出。请注意，下面的右移位是有符号符号扩展移位。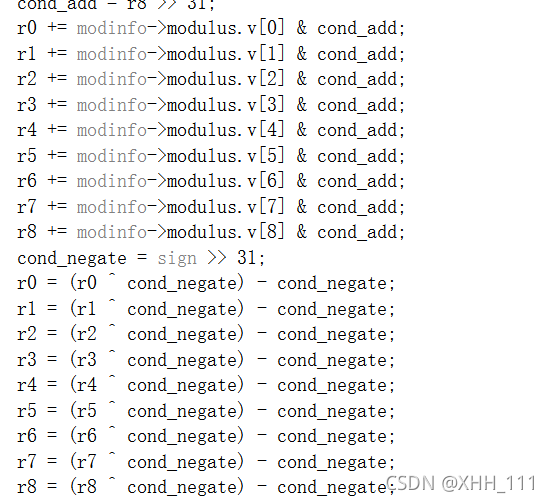
传播顶部位，使分支回到范围（-2^ 30,2^30）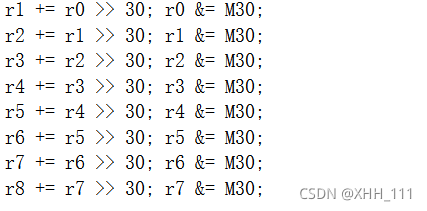
在第二步中，如果结果仍然为负，则再次添加模数，使r达到范围[0，模数）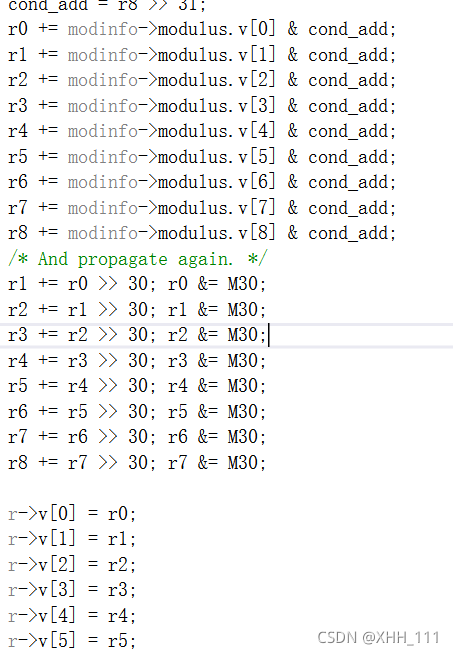
转移矩阵的数据类型
t=[u v]
[q r]
计算30步的转移矩阵和zeta。
输入：初始zeta
f0：初始f的底边
g0：初始g的底边
输出：t：转移矩阵
返回：最终zeta
实现解释中的divsteps\u n\u矩阵函数。
u、 v，q，r是正在建立的变换矩阵的元素，从单位矩阵开始。从语义上讲，它们是[-2^ 30,2^ 30]范围内的有符号整数，但在这里表示为无符号mod 2^ 32。这允许左移（对于负数为UB）。范围在[-2^ 31,2^31）内意味着对签名的铸造工作正常。
计算（zeta<0）和（g&1）的条件掩码。
计算x，y，z，f，u，v的条件求反版本
有条件地把x，y，z加到g，q，r上。
有条件地把g，q，r加到f，u，v上。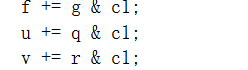
返回t中的数据和返回值
t的行列式必须是二的幂。这保证了与t相乘不会改变f和g的gcd，除了增加一个2的幂因子（将再次除以）。由于每个步骤的单个矩阵都有行列式2，因此其中30个步骤的总和将有行列式2^30
文章太长了，剩余部分放在下一篇博客来写。