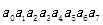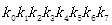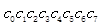在密码学中经常用到有限域的乘法,一般在AES中用到的是GF(2^8)有限域内乘法。什么是有限域呢?有限域通俗的讲就是函数的运算结果全都包含在一个域中,不同于实数域,有限域有一个最大值,所有超过这个最大值的数都会经过一定的方法使他回到这个域中,在密码学中应用很广泛,2^8意味着这个域的最大值是256.
以下代码是GF(2^8)有限域内乘法的C代码实现:
unsigned char XTIME(unsigned char x) {
return ((x << 1) ^ ((x & 0x80) ? 0x1b : 0x00));
}
unsigned char multiply(unsigned char a, unsigned char b) {
unsigned char temp[8] = { a };
unsigned char tempmultiply = 0x00;
int i = 0;
for (i = 1; i < 8; i++) {
temp[i] = XTIME(temp[i - 1]);
}
tempmultiply = (b & 0x01) * a;
for (i = 1; i <= 7; i++) {
tempmultiply ^= (((b >> i) & 0x01) * temp[i]);
}
return tempmultiply;
}
以下讲一下乘法的原理:
在二进制中,所有的数都能用0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80异或得到,0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80的二进制表示如下:
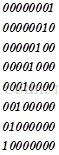
后一个分别是前一个的2倍。假设任意一个数a,他的二进制表示为10101101,可以由以下组合组成:
![]()
而任何一个数x和a相乘都可以表示为
所以只要计算出
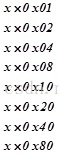
一切乘法的结果都可以得到。
XTIME函数的含义是求一个数x与0x02的乘积,一般求一个数的2倍,都是作移一位,在有限域内,要计算有限域的乘法,必须先确定一个GF上的8次不可约多项式,Rijndael密码中,这个多项式确定为x^8+x^4+x^3+x+1,如果最高位是1的话,左移一位的同时要异或0x1B,是因为最高位是1的话,再继续左移会超出域的最大值,这个时候需要取除以同余式,也就是异或0x1B。
for (i = 1; i < 8; i++) {
temp[i] = XTIME(temp[i - 1]);
}
for (i = 1; i <= 7; i++) {
tempmultiply ^= (((b >> i) & 0x01) * temp[i]);
}
另一个乘数b右移一位和0x01与运算,分别和这8个字符相乘,再把相乘的结果异或。就得到了a和b相乘的结果。
接下来举个例子:
求0x3a*0x24?首先0x3a=00111010,分别求
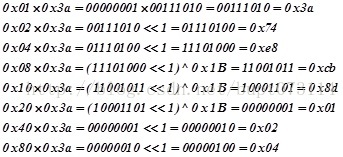
是正确结果。
如果要提高算法的计算效率,还可以这么做。
如果一个乘数的二进制可以表示为
一个乘数表示为
那么a的倍数关系可表示为:
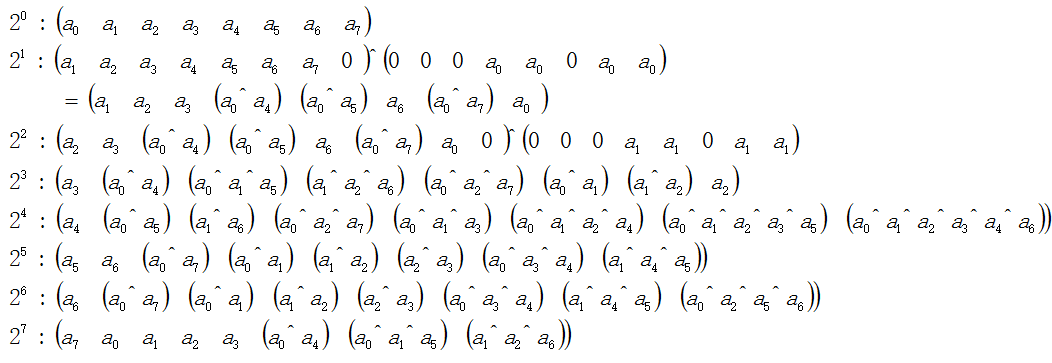
那么他的乘积可以表示为
其中
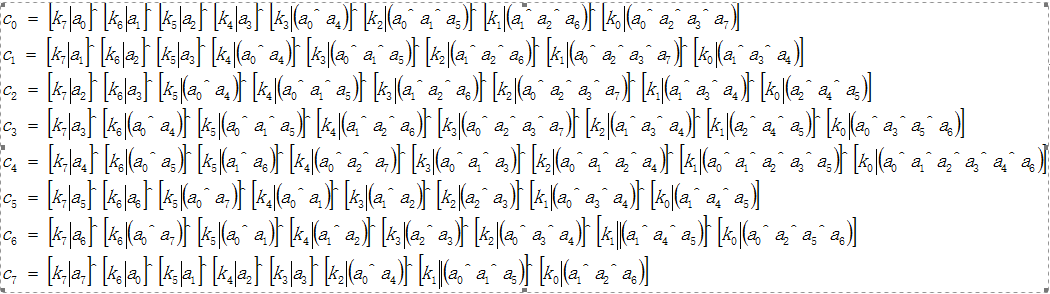
所以乘法可以表示为
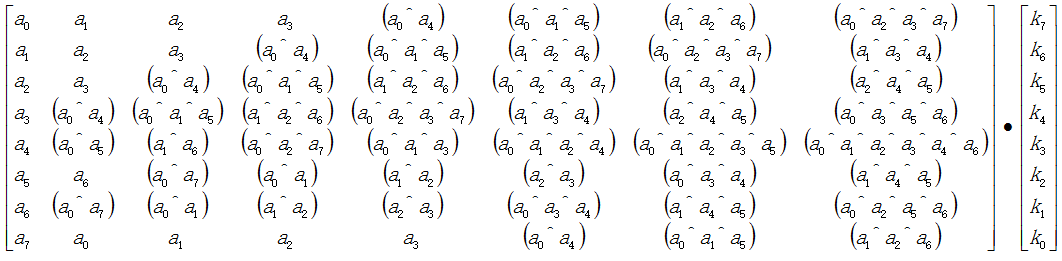
所以还有一种计算方法,那就是按照上面这个矩阵乘法。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void print_bit(bool *hexbit, int len) {
int i = 0;
for (i = 0; i < len; i++) {
printf("%x ", hexbit[i]);
}
}
void print_matrix(bool matrix[8][8]) {
int i = 0;
for (i = 0; i < 8; i++) {
print_bit(matrix[i], 8);
printf("\n");
}
}
void convertto_bit(unsigned char cipher, bool *hexbit, int len) {
len = 8;
int i = 0;
for (i = 0; i < 8; i++) {
if (cipher & 0x80) {
hexbit[i] = true;
}
cipher = cipher << 1;
}
}
void convertto_matrix(bool hexbit[8], bool matrix[8][8]) {
matrix[0][0] = hexbit[0];
matrix[0][1] = hexbit[1];
matrix[0][2] = hexbit[2];
matrix[0][3] = hexbit[3];
matrix[0][4] = hexbit[0] ^ hexbit[4];
matrix[0][5] = hexbit[0] ^ hexbit[1] ^ hexbit[5];
matrix[0][6] = hexbit[1] ^ hexbit[2] ^ hexbit[6];
matrix[0][7] = hexbit[0] ^ hexbit[2] ^ hexbit[3] ^ hexbit[7];
matrix[1][0] = hexbit[1];
matrix[1][1] = hexbit[2];
matrix[1][2] = hexbit[3];
matrix[1][3] = matrix[0][4];
matrix[1][4] = matrix[0][5];
matrix[1][5] = matrix[0][6];
matrix[1][6] = hexbit[0] ^ hexbit[2] ^ hexbit[3] ^ hexbit[7];
matrix[1][7] = hexbit[1] ^ hexbit[3] ^ hexbit[4];
matrix[2][0] = hexbit[2];
matrix[2][1] = hexbit[3];
matrix[2][2] = matrix[1][3];
matrix[2][3] = matrix[1][4];
matrix[2][4] = matrix[1][5];
matrix[2][5] = matrix[1][6];
matrix[2][6] = matrix[1][7];
matrix[2][7] = hexbit[2] ^ hexbit[4] ^ hexbit[5];
matrix[3][0] = hexbit[3];
matrix[3][1] = matrix[2][2];
matrix[3][2] = matrix[2][3];
matrix[3][3] = matrix[2][4];
matrix[3][4] = matrix[2][5];
matrix[3][5] = matrix[2][6];
matrix[3][6] = matrix[2][7];
matrix[3][7] = hexbit[0] ^ hexbit[3] ^ hexbit[5] ^ hexbit[6];
matrix[4][0] = hexbit[4];
matrix[4][1] = hexbit[0] ^ hexbit[5];
matrix[4][2] = hexbit[1] ^ hexbit[6];
matrix[4][3] = hexbit[0] ^ hexbit[2] ^ hexbit[7];
matrix[4][4] = hexbit[0] ^ hexbit[1] ^ hexbit[3];
matrix[4][5] = hexbit[0] ^ hexbit[1] ^ hexbit[2] ^ hexbit[4];
matrix[4][6] = hexbit[0] ^ hexbit[1] ^ hexbit[2] ^ hexbit[3] ^ hexbit[5];
matrix[4][7] = hexbit[0] ^ hexbit[1] ^ hexbit[2] ^ hexbit[3] ^ hexbit[4]
^ hexbit[6];
matrix[5][0] = hexbit[5];
matrix[5][1] = hexbit[6];
matrix[5][2] = hexbit[0] ^ hexbit[7];
matrix[5][3] = hexbit[0] ^ hexbit[1];
matrix[5][4] = hexbit[1] ^ hexbit[2];
matrix[5][5] = hexbit[2] ^ hexbit[3];
matrix[5][6] = hexbit[0] ^ hexbit[3] ^ hexbit[4];
matrix[5][7] = hexbit[1] ^ hexbit[4] ^ hexbit[5];
matrix[6][0] = hexbit[6];
matrix[6][1] = matrix[5][2];
matrix[6][2] = matrix[5][3];
matrix[6][3] = matrix[5][4];
matrix[6][4] = matrix[5][5];
matrix[6][5] = matrix[5][6];
matrix[6][6] = matrix[5][7];
matrix[6][7] = hexbit[0] ^ hexbit[2] ^ hexbit[5] ^ hexbit[6];
matrix[7][0] = hexbit[7];
matrix[7][1] = hexbit[0];
matrix[7][2] = hexbit[1];
matrix[7][3] = hexbit[2];
matrix[7][4] = hexbit[3];
matrix[7][5] = matrix[2][2];
matrix[7][6] = matrix[2][3];
matrix[7][7] = matrix[2][4];
return;
}
unsigned char XTIME(unsigned char x) {
return ((x << 1) ^ ((x & 0x80) ? 0x1b : 0x00));
}
unsigned char multiply(unsigned char a, unsigned char b) {
unsigned char temp[8] = { a };
unsigned char tempmultiply = 0x00;
int i = 0;
for (i = 1; i < 8; i++) {
temp[i] = XTIME(temp[i - 1]);
}
tempmultiply = (b & 0x01) * a;
for (i = 1; i <= 7; i++) {
tempmultiply ^= (((b >> i) & 0x01) * temp[i]);
}
return tempmultiply;
}
unsigned char multiply_bit(unsigned char plaintext, unsigned char key) {
int ret_len = 0;
bool plaintext_hexbit[8] = { false, false, false, false, false, false,
false, false };
bool key_hexbit[8] = { false, false, false, false, false, false, false,
false };
bool cipher_hexbit[8] = { false, false, false, false, false, false, false,
false };
//把plaintext转换成二进制
convertto_bit(plaintext, plaintext_hexbit, ret_len);
bool matrix[8][8] = { };
convertto_matrix(plaintext_hexbit, matrix);
//把key转换成二进制
convertto_bit(key, key_hexbit, ret_len);
//print_matrix(matrix);
//printf("\n");
//print_bit(key_hexbit, sizeof(key_hexbit));
//printf("\n");
int i = 0;
int j = 0;
for (i = 0; i < 8; i++) {
cipher_hexbit[i] = false;
for(j = 0;j < 8;j++) {
if(key_hexbit[j]){
cipher_hexbit[i] ^=matrix[i][7-j];
}
}
}
//print_bit(cipher_hexbit, sizeof(cipher_hexbit));
unsigned char outcome = 0;
for (i = 0; i < 8; i++) {
if (cipher_hexbit[i]) {
outcome ^= 0x01 << (7 - i);
}
}
return outcome;
}
int main(int argc, char * argv[]) {
unsigned char plaintext = 0x49;
unsigned char key = 0x24;
printf("%#x", multiply_bit(plaintext, key));
printf("\n");
// unsigned char plaintext1 = 0x01;
// unsigned char key1 = 0x21;
printf("%#x", multiply(plaintext, key));
return 0;
}输出结果是
0xdc
0xdc经过测试,后一种方法比第一种方法效率慢很多,原因是其中代码计算矩阵和矩阵乘法比第一种方法复杂。但是第二种提供另外一种思路。