2021SC@SDUSC
在比特币流行之前,secp256k1几乎从未被使用过,但由于其几个不错的特性,它现在越来越受欢迎。secp256k1本身就是一个被限定参数的椭圆曲线方程,就像一次函数一般写作 y = a x + b y=ax+by=ax+b,但我限定参数a=1,b=1就会得到一个特定的一次函数 y = x + 1 y=x+1y=x+1,我可以给 y = x + 1 y=x+1y=x+1起一个新的名字,但没有必要,因为这个函数没有很多场景要用到它,但一个被限定参数的椭圆曲线方程就有一个名字,叫secp256k1。给它取个名字的原因很简单,就是因为比特币区块链场景下经常用。由于大多数常用的曲线都具有随机结构,但secp256k1是以这种特殊的非随机方式构建的,使得secp256k1可以实现特别高效的计算。因此,如果实现充分优化,它通常比其他曲线快 30%以上。
既然secp256k1就是椭圆曲线,那我们就可以从椭圆曲线的一般方程入手,了解椭圆曲线的几个性质,并进一步将其引入到特殊的secp256k1中。在比特币架构中的非对称加密实现使用的就是ECDSA(椭圆曲线数字签名算法)椭圆曲线,曲线的参数就是采用secp256k1算法生成。
实际上ECDSA使用的模运算等过程注定ECDSA只能使用离散的整数点(否则无法取模运算),但椭圆曲线的数学方程实际上是一个连续的椭圆曲线(y 2 = x 3 + a x + b y^2 = x^3 +ax + by2=x3+ax+b 其中x,y∈R),我们的加密和数字签名过程需要将其应用在有限域(有限域中的椭圆曲线上的点和其上定义的运算构成的群含有限离散点,且点的横纵坐标均为有限域中的元素,详见下篇博客)中。如果直接开始说有限域可能会有些概念上的困难,因此本篇文章中我会先介绍连续的椭圆曲线(即实数域下的椭圆曲线)上的基本运算,实数域椭圆曲线的很多性质其实与有限域的椭圆曲线一致,在下一篇中我会将椭圆曲线方程应用到有限域中。
ECC原理
群
由于椭圆曲线的点加法和点乘法离不开群的相关概念,在此我提一下,如果是离散数学学的比较好的朋友可以跳过本部分。
群G只定义一个二元运算,即两个元素对一个运算符号的运算。群满足四个基本条件:封闭性、结合律、单位元、逆元。
封闭性:G中两元素的运算结果还在这个群中。
结合律:对G中任意元素a、b、c,都有a·(b·c)=(a·b)·c
单位元:对单位元e,G中任意元素a都有a·e=e·a=a成立
逆元:对G中任意元素a,G中都存在一个元素a’,使得a·a’=a’·a=e成立
椭圆曲线几何加法
事实上,椭圆曲线的点集和在椭圆曲线上定义的加法运算(即几何加法)就可以看作一个群,而且是一个交换群(上述四个条件外满足交换律)。
椭圆曲线点加法即在椭圆曲线上任取两点P和Q,将P和Q两点连线,交椭圆曲线于一点,该点关于x轴在椭圆曲线上的对称点R即为P+R的运算结果(P和R做椭圆曲线点加法)。这样说可能会比较抽象,大家可以在这个链接中输入相应参数体验这个过程: https://andrea.corbellini.name/ecc/interactive/reals-add.html
下面我附图来详细讲解这个运算过程: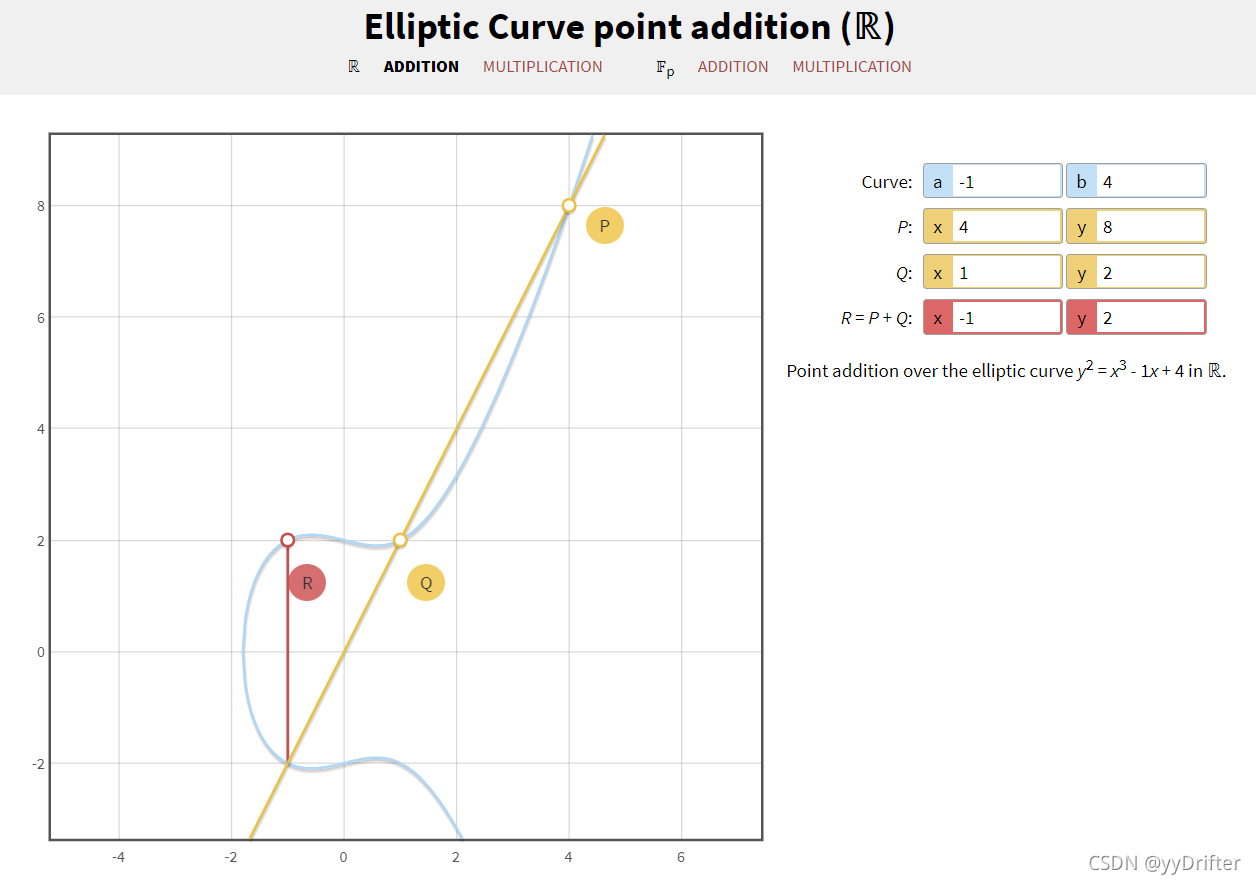
这个图中就可以比较直观看到椭圆曲线点加法的运算过程,椭圆曲线方程为:
y 2 = x 3 + a x + b y^2=x^3+ax+by2=x3+ax+b
演示图中右侧最上面两个参数a和b即为对应椭圆曲线方程中的两个参数,也就说,这两个参数确定了,椭圆曲线的样子也就唯一确定了。下面是P和Q,P和Q是我们在椭圆曲线上任意找到的两个点,这两个点的连线会交椭圆曲线于一点,由于椭圆曲线方程的性质决定椭圆曲线必关于x轴对称,因此我们很容易找到交点关于x轴的对称点R,于是我们就可以说:P+Q=R。
前面提到,椭圆曲线的点集和在椭圆曲线上定义的加法运算就可以看作一个交换群,于是我们有对椭圆曲线上任意三点A、B、C三点,有A+(B+C)=(A+B)+C成立(结合律),A+B=B+A(交换律)。对于单位元我们定义一个位于无穷远处的点为单位元,记作0,那么有A+0=0+A=A。相应地我们定义逆元,A的逆元A’即为-A,-A在椭圆曲线上的几何表述即为A点关于x轴在椭圆曲线上的对称点,我们有A+ -A=-A +A=0,由此也可以理解为椭圆曲线上点A和A关于x轴对称点连成的线(实际上就是过A点垂直于x轴的直线)与椭圆曲线的交点,这个交点关于x轴的对称点是一个无穷远点。
虽然我们通过上面图片可以直观感受到了这个运算过程,但需要给出数学表达式的代数加法计算过程,对于给定的公式如果耐心算的话求解不会很困难,这里给出计算过程:
对 非 0 , 非 对 称 点 P 和 Q , 令 P ( x P , y P ) , Q ( x Q , y Q ) 则 斜 率 m = y P − y Q x P − x Q 则 满 足 R = P + Q 的 点 R ( x R , y R ) : x R = m 2 − x P − x Q y R = − [ y P + m ( x R − x P ) ] 对非0,非对称点P和Q,令 P(x_P,y_P) , Q(x_Q,y_Q)\\ 则斜率m=\frac{y_P - y_Q}{x_P - x_Q}\\ 则满足R=P+Q的点R(x_R,y_R) :\\ x_R=m^2-x_P-x_Q\\ y_R=-[y_P+m(x_R-x_P)]对非0,非对称点P和Q,令P(xP,yP),Q(xQ,yQ)则斜率m=xP−xQyP−yQ则满足R=P+Q的点R(xR,yR):xR=m2−xP−xQyR=−[yP+m(xR−xP)]
椭圆曲线标量乘法
理解了椭圆曲线几何加法之后理解标量乘法就比较容易了,这里定义n为一整数,对于椭圆曲线上任取一点P有n·P=P+P+…+P(n个P进行椭圆曲线几何加法运算),最终结果一定是椭圆曲线上一点,可以证明:椭圆曲线对几何加法封闭,则P+P得到结果必为椭圆曲线上一点,该椭圆曲线上的点+P结果必然还在椭圆曲线上……以此类推。不妨另n·P运算结果点为Q,则Q必为椭圆曲线上一点。那么我们就得到了椭圆曲线上标量乘法运算Q = n·P。
大家可以在这个链接中输入相应参数体验这个过程:https://andrea.corbellini.name/ecc/interactive/reals-mul.html.下面附图: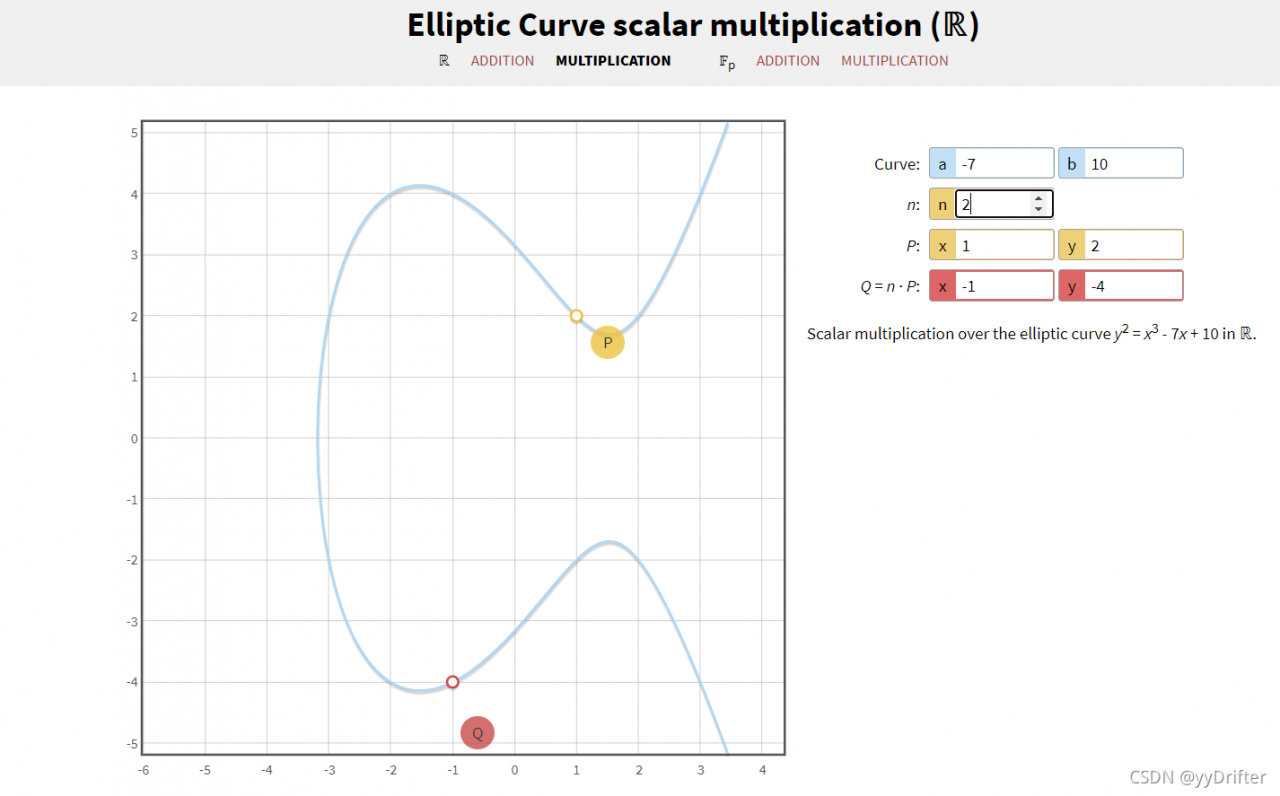
可以看到给定参数a、b的椭圆曲线上任意一点P的标量乘运算结果。同时我们意识到标量乘法本质上还是几何加法。那么我们有:
1·P=P,即P点不经过任何运算还是P点
0·P=0,即0·P得到的点为无穷远点
-1·P=-P,即-1·P·P得到的点为P点的逆元
关于数学运算,对2·P而言,即为P+P,在图上理解为P和P组成连线与椭圆曲线的交点关于x轴的对称点,由于P和P重合,那么这个连线实际上就是一条切线。下面我给出计算2·P的代数加法公式:
令 椭 圆 曲 线 上 一 点 P ( x P , y P ) 则 过 点 P 切 线 斜 率 m = 3 x P 2 + a 2 y P 则 满 足 Q = 2 P 的 点 Q ( x Q , y Q ) : x Q = m 2 − 2 x P y Q = − [ y P + m ( x Q − x P ) ] 令椭圆曲线上一点P(x_P,y_P)\\ 则过点P切线斜率m=\frac{3x_P^2+a}{2y_P}\\ 则满足Q=2P的点Q(x_Q,y_Q):\\ x_Q=m^2-2x_P\\y_Q=-[y_P+m(x_Q-x_P)]令椭圆曲线上一点P(xP,yP)则过点P切线斜率m=2yP3xP2+a则满足Q=2P的点Q(xQ,yQ):xQ=m2−2xPyQ=−[yP+m(xQ−xP)]
计算标量乘法运算Q = n·P你可以用我证明的方法让P一个个加得到正确的Q点,但同时也可以想到,n个相同P的相加可以采用一些简单的算法,即先做倍数再做加法:如n=151时,151·P可以将151看作2 0 + 2 1 + 2 2 + 2 4 + 2 7 2^0 + 2^1 + 2^2 + 2^4 + 2^720+21+22+24+27,可以先获取P;取P的2倍,得到2P;2P加上P;把2P再取2倍,得到4P;4P加上2P加上P;4P再取2倍,得到8P;不取8P做运算;8P取2倍,得到16P;16P加上4P加上2P加上P得到Q,这个过程可以大大减少我们计算的步骤,尤其是在n非常大的情况下。
在本篇中我们可以看到,连续椭圆曲线上的点和椭圆曲线上的几何加法运算可以构成一个群,标量乘法本质上还是几何加法,不过是因为我们常用它而给他单独起了一个新名字罢了,否则这个群上就定义两个运算而变成环或域了。在有限域上的椭圆曲线上的点和椭圆曲线上的几何加法运算也可以构成一个群,但同时也具有了一些新的性质。下一篇博客中我会对有限域和有限域上椭圆曲线的一些性质加以说明。