引言
1.机器视觉中常用的有两种不同类型的镜头：普通镜头和远心镜头。使用普通镜头时，世界坐标系到图像坐标系为透视投影；使用远心镜头时为平行投影。
2.通常将世界坐标系原点放在双目立体系统的左相机中心。
3.世界坐标系--->相机坐标系--->成像平面坐标系--->像素坐标系
4.影像坐标系--->相机坐标系--->世界坐标系
5.张氏相机标定法
世界坐标系到相机坐标系
从世界坐标系到相机坐标系， 这是一个刚体变换，只需对世界坐标系的三维点作用一个旋转R和平移t（R，t即为相机的外参），变换过程可以通过一下公式完成：
相机坐标系到成像平面坐标系
这一过程进行了从三维坐标到二维坐标的转换，也即投影透视过程（用中心投影法将物体投射到投影面上，从而获得的一种较为接近视觉效果的单面投影图，也就是使我们人眼看到景物近大远小的一种成像方式）。
成像过程如下图所示：针孔面（相机坐标系）在图像平面（图像坐标系）和物点平面（棋盘平面）之间，所成图像为倒立实像。
但是为了在数学上更方便描述，我们将相机坐标系和图像坐标系位置对调，变成下图所示的布置方式（没有实际的物理意义，只是方便计算）：
此时，假设相机坐标系中有一点M，则在理想图像坐标系下（无畸变）的成像点P的坐标为（可由相似三角形原则得出）：
--->
成像平面坐标系到像素坐标系（计算机视觉，不考虑摄影测量学）
如上图，成平面坐标系和像素坐标系之间存在一个缩放和平移
+--->
--->
其中
α、β的单位为像素/米;
fx、fy为x、y方向的焦距，单位为像素;
(cx,cy)为主点，图像的中心，单位为像素。
那么，相机坐标系到像素坐标系的最终形式可写成：
将 Zc移到左边：
所以，在世界坐标系中的三维点M=[X,Y,Z]T 和像素坐标系中二维点m=[u,v]T的关系为：
即：
其中，s为缩放因子，A为相机的内参矩阵，[R t]为相机的外参矩阵，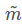
和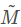
分别为m和M对应的齐次坐标。
版权声明：本文为sinat_29634715原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。