基本的组合数学公式

加法法则和乘法法则

加法法则：事件A与事件B的发生是和互不影响的，则事件A或者B发生的次数为两者之和。

乘法法则：事件A和事件B的发生是串行的，则两者发生的次数为两者之积。

排列与组合

排列与组合问题包含四个子问题——集合的排列，集合的组合，多重集合的排列，多重集合的组合。

定义：设S为n元集。

①从S中有序的选取r个元素称为S的一个r排列。S的不同的r排列组合总数记为P（n,r）。r=n时的排列称作S的全排列。

②从S中无序的选取r个元素称作S的一个r组合.S的不同的r组合总数记为C（n,r）。

排列是有序的，组合是无序的，这是排列跟组合最大的区别，由此也可以得出两者的推到公式。

显然对于排列数P（n,r）=n×（n-1）×（n-2）×…… x(n-r+1)；

由于P（n,r）=C（n,r）×n！，故C（n,r）=P（n,r）/n！;

多重集：

组合数学中比较有趣的东西：

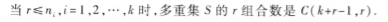
证明：

非降路径问题

栈操作中输出的组合数目