因为实习,耽搁了些许时间,这是上一篇的未完成部分。特此补上。
本文要解决的有两个问题:
1. LR和ME(最大熵)的关系
2. LR的并行化
把这两个问题分开来学习,也是因为这里边的内容较多,理解起来也更费劲。好了,直奔主题。
先来看ME最大熵模型。首先需要理解的是最大熵的原理。一句话概括就是:在学习概率模型时,熵最大的模型就是最好的模型。
此处需要注意的是,这里的概率模型空间并不是随意取的,而是在一定的约束条件在选取的,所以也可以将最大熵原理表述为:在满足约束条件下的模型集合中选取熵最大的模型。
接下来看看最大熵模型的定义。

则我们说模型集合C中,使得H(p)熵最大的模型就是最大熵模型。
我们说逻辑斯蒂回归模型和ME模型都能用来做二分类和多分类问题;他们又都属于对数线性模型;而且一般都采用极大似然估计求解。既然有这么多的相似之处,那么他们之间存在着什么关系呢?
接下来我们就从数学推倒的角度来彻底的分析一番。
首先我们先设定一些基本符号概念:

再次,我们对逻辑斯蒂的二分类模型一般化,则有: 
此时二分类的逻辑斯蒂模型求解问题就变成了多分类模型的求解问题。 
对数似然函数的偏导求解较为复杂,大家私下可手动推一下。。。
最大化似然函数,也就是取偏导为0时的参数,我们看看偏导为0时会发现什么。即: 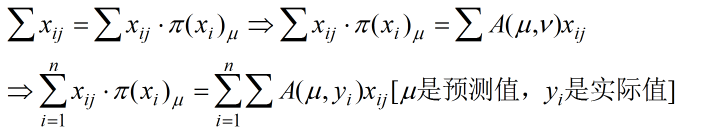
上述是对逻辑斯蒂回归的理论分析,接下来我们来看看最大熵模型。
要想弄清楚最大熵和逻辑斯蒂模型之间的关系,最直接的办法就是找寻他们的概率分布函数之间的关系。上边已经给出了最大熵模型的数学定义,现在我们来看看怎么求解这一模型。
最大熵模型的学习等价于约束最优化问题,即:
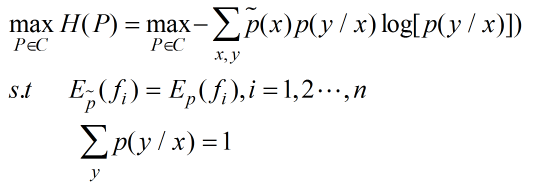
因为一般最优化问题都市最小化,所以可以将上述问题等价为最小化问题,即:
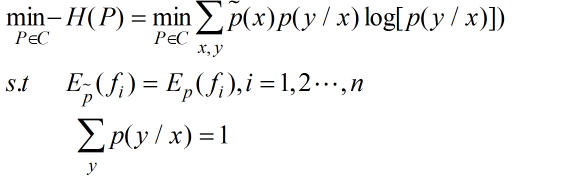
因为存在约束条件,而求解约束最优化问题可以通过引入拉格朗日乘子来解决,从而将约束的最优化问题转化为无约束的最优化问题。好,我们接下来看看会发现什么。。。
首先引入拉格朗日乘子。定义拉格朗日函数:
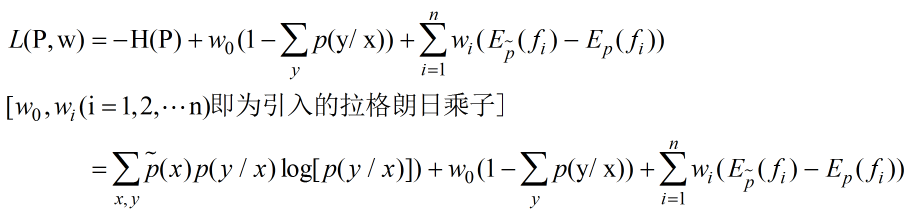
此外,似然函数的最大化已然转换成最小化问题,而想借助构建的拉格朗日函数求解这一最小化问题,也就变成了先对拉格朗日函数求最大化,然后再最小化,即:
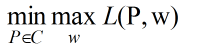
依据拉格朗日的对偶特性,其对偶问题是: ![]()
这时我们就可以先求解最小化问题,记为: 
具体求解过程如下: 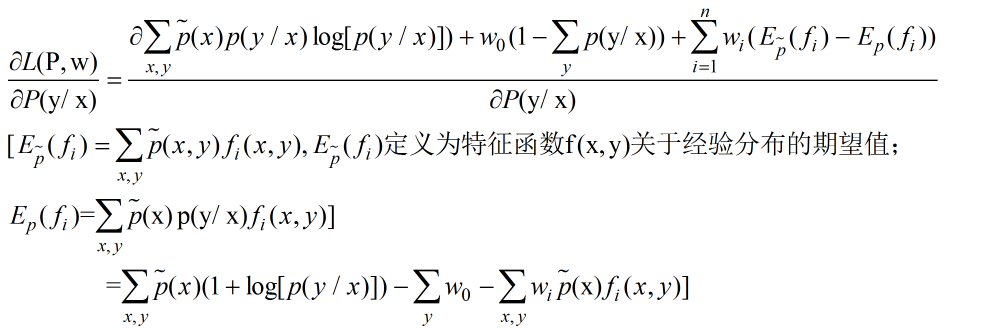
令偏导为0,得到: 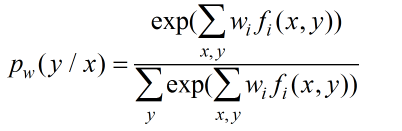
这也就证明了逻辑斯蒂回归是最大熵模型的一个特例。
好好好,终于解决了一个大难题。接下俩我们看看LR的并行化实现。。。
在此我就不普及并行化的概念和意义所在了,不太清楚的请自行私下啃书脑补。
并行化计算将分为两大部分讲解:
1. 数据分割
2. 并行计算
先来看看数据分割的问题。LR中最基本也是最关键的步骤就是梯度计算,而很多诸如改进迭代尺度法、牛顿法、拟牛顿法等都是对梯度计算的优化,由此,并行化其实也是对目标函数的梯度计算的一种优化方法。
通过前边的梯度计算公式,我们知道,计算只涉及到向量间的点积和加减,而这些基本操作都可以很容易的在每次迭代过程中分拆为相互独立的计算步骤。不同节点进行独立的计算,然后将结果归并起来。
最简单的并行计算就是按行并行的方法,即将样本矩阵按行划分,将样本特征向量分到不同的计算节点。但在针对高维特征向量做计算时,需要对它们进行逻辑回归,因此还需要将高维特征向量拆分为若干小向量进行求解。
先来谈谈怎么做数据分割。假设所有计算节点排列成M行N列,按行划分,每个计算节点分配m/M个样本特征向量和分类标签;按列划分,则每个计算节点分配n/N个样本特征向量和分类标签。如下图所示。 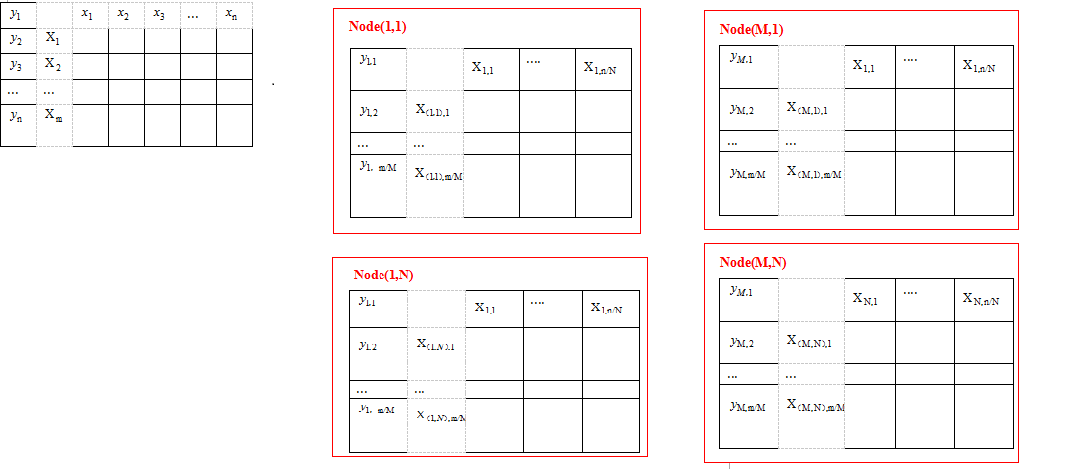
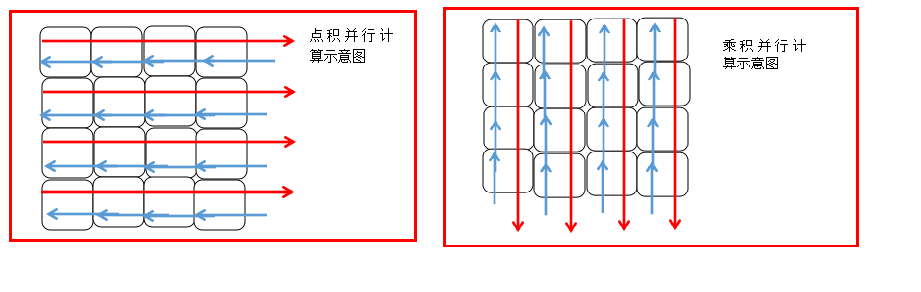
由梯度计算可知,其计算结果依赖于两大项计算单元:权值向量和特征向量的点积+标量和特征向量的乘积。这样就可以将梯度计算分为两个并行计算步骤,然后再归并结果。
具体步骤如下:
- 各节点并行计算权值向量和特征向量之间的点积;
- 对行号相同的的节点计算结果进行归并;
- 各节点独立计算标量和特征向量之间的乘积;
对列号相同的节点计算结果进行归并;
整个并行计算的流程图如下: 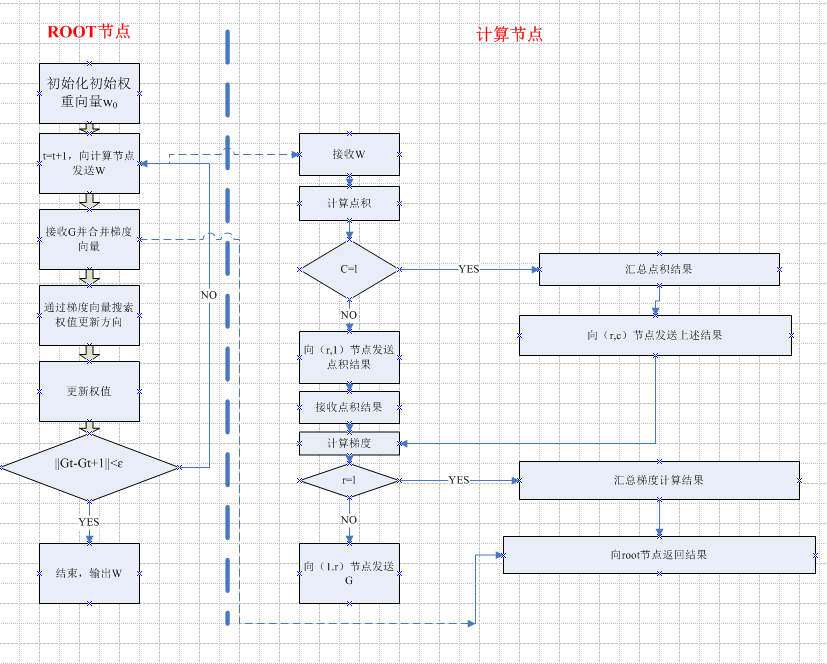
PS:关于LR的并行计算仍在学习中,这里也只是浅尝辄止,后边会继续就这一块做更详细的学习和总结。
PPS:关于LR的主题暂且告一段落。后续将是Paper的阅读和其他算法的个人理解和总结.
参考资料:
【1】http://blog.csdn.net/cyh_24/article/details/50359055
【2】http://blog.sina.com.cn/s/blog_6cb8e53d0101oetv.html
【3】统计机器学习(李航)
【4】Deep Learning(Yoshua Bengio & Ian Goodfellow & Aaron Courville)