本文介绍了皮尔逊(Pearson)相关系数,其手动计算以及通过Pythonnumpy模块进行的计算。
皮尔逊相关系数测量变量之间的线性关联。它的值可以这样解释:
- +1-完全正相关
- +0.8-强正相关
- +0.6-中等正相关
- 0-无关联
- -0.6-中度负相关
- -0.8-强烈的负相关
- -1-完全负相关
我们将说明相关系数如何随不同类型的关联而变化。在本文中,我们还将显示零关联并不总是意味着零关联。非线性相关变量的相关系数可能接近零。
皮尔逊相关系数是多少?
皮尔逊相关系数也称为皮尔逊积矩相关系数。它是两个随机变量X和Y之间线性关系的度量。在数学上,如果(σXY)是X和Y之间的协方差,并且(σX)是X的标准偏差,则皮尔逊相关系数 ρ可以由下式给出:
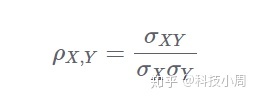
由于协方差总是小于各个标准偏差的乘积,因此ρ的值在-1和+1之间变化。从上面我们还可以看到,变量与自身的相关性为1:
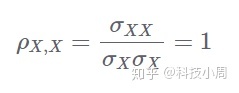
在开始编写代码之前,让我们做一个简短的示例,看看如何计算该系数。
皮尔逊相关系数如何计算?
假设我们对随机变量X和Y有一些观察。如果您打算从头开始实施所有工作或进行一些手动计算,那么在给定X和Y时需要以下内容:

让我们使用以上内容来计算相关性。我们将使用协方差和标准偏差的有偏估计。这不会影响正在计算的相关系数的值,因为观察值的数量在分子和分母中抵消了:
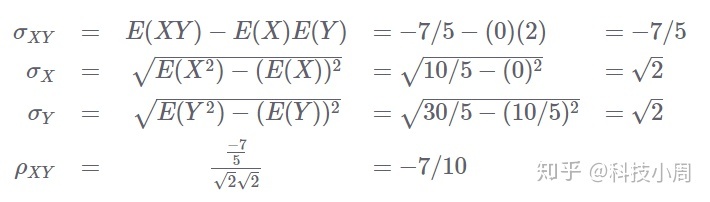
使用Numpy的Python中的Pearson相关系数
皮尔逊相关系数可以使用corrcoef()Numpy中的方法在Python中计算。
此函数的输入通常是一个矩阵,例如size mxn,其中:
- 每列代表一个随机变量的值
- 每行代表一个
n随机变量样本 n代表不同随机变量的总数m代表每个变量的样本总数
对于n随机变量,它返回一个nxn方矩阵M,其中M(i,j)指示了随机变量i和之间的相关系数j。由于变量与变量自身之间的相关系数为1,因此所有对角线项(i,i)均等于1。
简而言之:
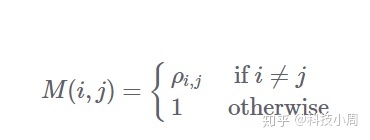
注意,相关矩阵是对称的,因为相关是对称的,即中号(一世,Ĵ)=中号(Ĵ,一世)中号(一世,Ĵ)=中号(Ĵ,一世)。让我们以上一节中的简单示例为例,看看如何使用C要么[RCØËF()C要么[RCØËF()与ν米pÿν米pÿ。
首先,让我们导入该numpy模块以及pyplotMatplotlib中的模块。稍后,我们将使用Matplotlib可视化相关性:
import numpy as np
import matplotlib.pyplot as plt我们将从以前的示例中使用相同的值。让我们将其存储x_simple并计算相关矩阵:
x_simple = np.array([-2, -1, 0, 1, 2])
y_simple = np.array([4, 1, 3, 2, 0])
my_rho = np.corrcoef(x_simple, y_simple)
print(my_rho)以下是输出相关矩阵。注意对角线上的那些,表明变量与自身的相关系数为1:
[[ 1. -0.7]
[-0.7 1. ]]正负相关示例
让我们可视化一些关系的相关系数。首先,我们将在两个变量之间具有完全正相关(+1)和完全负相关(-1)。然后,我们将生成两个随机变量,因此相关系数应始终接近零,除非随机性偶然具有某些相关性,而这种可能性极小。
我们将使用a,seed以便在RandomState从Numpy调用the时此示例可重复:
seed = 13
rand = np.random.RandomState(seed)
x = rand.uniform(0,1,100)
x = np.vstack((x,x*2+1))
x = np.vstack((x,-x[0,]*2+1))
x = np.vstack((x,rand.normal(1,3,100)))第一次rand.uniform()调用会生成随机均匀分布:
[7.77702411e-01 2.37541220e-01 8.24278533e-01 9.65749198e-01
9.72601114e-01 4.53449247e-01 6.09042463e-01 7.75526515e-01
6.41613345e-01 7.22018230e-01 3.50365241e-02 2.98449471e-01
5.85124919e-02 8.57060943e-01 3.72854028e-01 6.79847952e-01
2.56279949e-01 3.47581215e-01 9.41277008e-03 3.58333783e-01
9.49094182e-01 2.17899009e-01 3.19391366e-01 9.17772386e-01
3.19036664e-02 6.50845370e-02 6.29828999e-01 8.73813443e-01
8.71573230e-03 7.46577237e-01 8.12841171e-01 7.57174462e-02
6.56455335e-01 5.09262200e-01 4.79883391e-01 9.55574145e-01
1.20335695e-05 2.46978701e-01 7.12232678e-01 3.24582050e-01
2.76996356e-01 6.95445453e-01 9.18551748e-01 2.44475702e-01
4.58085817e-01 2.52992683e-01 3.79333291e-01 6.04538829e-01
7.72378760e-01 6.79174968e-02 6.86085079e-01 5.48260097e-01
1.37986053e-01 9.87532192e-02 2.45559105e-01 1.51786663e-01
9.25994479e-01 6.80105016e-01 2.37658922e-01 5.68885253e-01
5.56632051e-01 7.27372109e-02 8.39708510e-01 4.05319493e-01
1.44870989e-01 1.90920059e-01 4.90640137e-01 7.12024374e-01
9.84938458e-01 8.74786502e-01 4.99041684e-01 1.06779994e-01
9.13212807e-01 3.64915961e-01 2.26587877e-01 8.72431862e-01
1.36358352e-01 2.36380160e-01 5.95399245e-01 5.63922609e-01
9.58934732e-01 4.53239333e-01 1.28958075e-01 7.60567677e-01
2.01634075e-01 1.75729863e-01 4.37118013e-01 3.40260803e-01
9.67253109e-01 1.43026077e-01 8.44558533e-01 6.69406140e-01
1.09304908e-01 8.82535400e-02 9.66462041e-01 1.94297485e-01
8.19000600e-02 2.69384695e-01 6.50130518e-01 5.46777245e-01]然后,我们可以调用vstack()将其他数组垂直堆叠到该数组。这样,我们可以在同一个x引用中堆叠一堆类似于上面的变量,并顺序访问它们。
在第一个均匀分布之后,我们在垂直方向上堆叠了一些变量集-第二个变量与第一个变量具有完全正相关,第三个变量与第一个变量具有完全负相关,第四个变量是完全随机的,因此它应该具有〜0的相关性。
当我们有一个这样的x引用时,我们可以通过将其单独传递给来计算垂直堆栈中每个元素的相关性np.corrcoef():
rho = np.corrcoef(x)
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(12, 3))
for i in [0,1,2]:
ax[i].scatter(x[0,],x[1+i,])
ax[i].title.set_text('Correlation = ' + "{:.2f}".format(rho[0,i+1]))
ax[i].set(xlabel='x',ylabel='y')
fig.subplots_adjust(wspace=.4)
plt.show()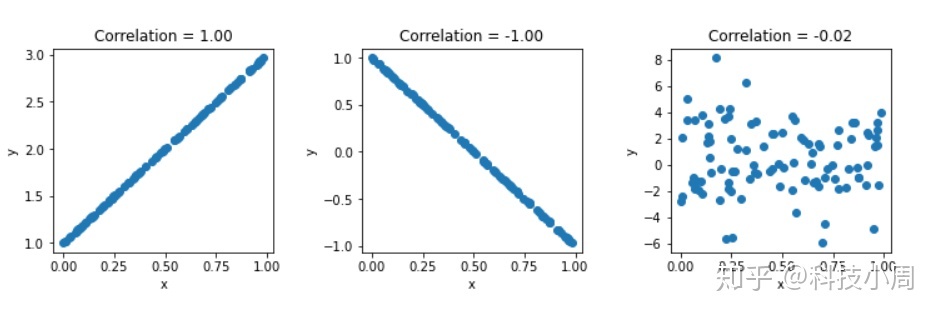
了解皮尔逊的相关系数变化
只是为了查看相关系数如何随两个变量之间的关系变化而变化,让我们向上x一节中生成的矩阵中添加一些随机噪声,然后重新运行代码。
在此示例中,我们将向关联图缓慢添加不同程度的噪声,并在每个步骤上计算关联系数:
fig, ax = plt.subplots(nrows=2, ncols=4, figsize=(15, 8))
for noise, i in zip([0.05,0.2,0.8,2],[0,1,2,3]):
# Add noise
x_with_noise = x+rand.normal(0,noise,x.shape)
# Compute correlation
rho_noise = np.corrcoef(x_with_noise)
# Plot column wise. Positive correlation in row 0 and negative in row 1
ax[0,i].scatter(x_with_noise[0,],x_with_noise[1,],color='magenta')
ax[1,i].scatter(x_with_noise[0,],x_with_noise[2,],color='green')
ax[0,i].title.set_text('Correlation = ' + "{:.2f}".format(rho_noise[0,1])
+ 'n Noise = ' + "{:.2f}".format(noise) )
ax[1,i].title.set_text('Correlation = ' + "{:.2f}".format(rho_noise[0,2])
+ 'n Noise = ' + "{:.2f}".format(noise))
ax[0,i].set(xlabel='x',ylabel='y')
ax[1,i].set(xlabel='x',ylabel='y')
fig.subplots_adjust(wspace=0.3,hspace=0.4)
plt.show()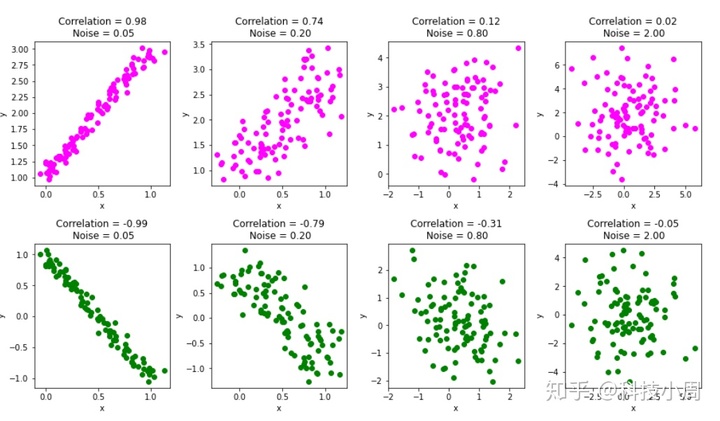
一个常见的陷阱:没有关联的关联
有一个普遍的误解,认为零相关意味着没有关联。让我们澄清一下,相关性严格衡量了两个变量之间的线性关系。
下面的示例显示了彼此非线性关联但具有零相关性的变量。
(y = e x)的最后一个示例具有约0.52的相关系数,这再次不反映两个变量之间的真实关联:
# Create a data matrix
x_nonlinear = np.linspace(-10,10,100)
x_nonlinear = np.vstack((x_nonlinear,x_nonlinear*x_nonlinear))
x_nonlinear = np.vstack((x_nonlinear,-x_nonlinear[0,]**2))
x_nonlinear = np.vstack((x_nonlinear,x_nonlinear[0,]**4))
x_nonlinear = np.vstack((x_nonlinear,np.log(x_nonlinear[0,]**2+1)))
x_nonlinear = np.vstack((x_nonlinear,np.exp(x_nonlinear[0,])))
# Compute the correlation
rho_nonlinear = np.corrcoef(x_nonlinear)
# Plot the data
fig, ax = plt.subplots(nrows=1, ncols=5, figsize=(16, 3))
title = ['$y=x^2$','$y=-x^2$','$y=x^4$','$y=log(x^2+1)$','$y=exp(x)$']
for i in [0,1,2,3,4]:
ax[i].scatter(x_nonlinear[0,],x_nonlinear[1+i,],color='cyan')
ax[i].title.set_text(title[i] + 'n' +
'Correlation = ' + "{:.2f}".format(rho_nonlinear[0,i+1]))
ax[i].set(xlabel='x',ylabel='y')
fig.subplots_adjust(wspace=.4)
plt.show()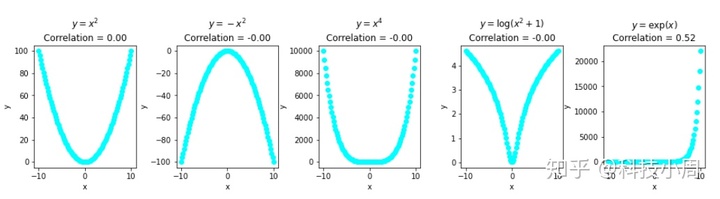
结论
在本文中,我们讨论了皮尔逊相关系数。我们使用了corrcoef()Pythonnumpy模块中的方法来计算其值。
如果随机变量具有较高的线性关联,则它们的相关系数接近+1或-1。另一方面,统计独立变量的相关系数接近零。
我们还证明了非线性关联可以具有零或接近零的相关系数,这意味着具有高关联性的变量可能不具有较高的Pearson相关系数值。