决策树
定义
决策树
- 分类决策树模型是表示基于特征对实例进行分类的树形结构。决策树可以转换成一个if-then规则的集合,也可以看作是定义在特征空间划分上的类的条件概率分布。
- 决策树学习旨在构建一个与训练数据拟合很好,并且复杂度小的决策树。因为从可能的决策树中直接选取最优决策树是NP完全问题。现实中采用启发式方法学习次优的决策树。决策树学习算法包括3部分:特征选择、树的生成和树的剪枝。常用的算法有ID3、 C4.5和CART。
- 特征选择的目的在于选取对训练数据能够分类的特征。特征选择的关键是其准则。常用的准则如下:
- 样本集合 ? 对特征 ? 的信息增益(ID3)
g ( D , A ) = H ( D ) − H ( D ∣ A ) H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log 2 ∣ C k ∣ ∣ D ∣ H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) \begin{gathered} g(D, A)=H(D)-H(D \mid A) \\ H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|} \\ H(D \mid A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right) \end{gathered}g(D,A)=H(D)−H(D∣A)H(D)=−k=1∑K∣D∣∣Ck∣log2∣D∣∣Ck∣H(D∣A)=i=1∑n∣D∣∣Di∣H(Di)
其中, H ( D ) H(D)H(D) 是数据集 D DD 的樀, H ( D i ) H\left(D_{i}\right)H(Di) 是数据集 D i D_{i}Di 的熵, H ( D ∣ A ) H(D \mid A)H(D∣A) 是数据集 D DD 对特征 A AA 的条件熵。 D i D_{i}Di 是 D DD 中特征 A AA 取第 i ii 个值的样本子集, C k C_{k}Ck 是 D DD 中属于第 k kk 类 的样本子集。 n nn 是特征 A AA 取 值的个数, K KK 是卖的个数。
2.样本犨合 D DD 对特征 A AA 的信自增益比 (C4.5)
g R ( D , A ) = g ( D , A ) H ( D ) g_{R}(D, A)=\frac{g(D, A)}{H(D)}gR(D,A)=H(D)g(D,A)
其中, g ( D , A ) g(D, A)g(D,A) 是信自增益, H ( D ) H(D)H(D) 是数据集 D DD 的熵。
3.样本集合 D DD 的基尼指数 (CART)
Gini ( D ) = 1 − ∑ k = 1 K ( ∣ C k ∣ ∣ D ∣ ) 2 \operatorname{Gini}(D)=1-\sum_{k=1}^{K}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2}Gini(D)=1−k=1∑K(∣D∣∣Ck∣)2
特征 A AA 条件下集合 D DD 的基尼指数:
Gini ( D , A ) = ∣ D 1 ∣ ∣ D ∣ Gini ( D 1 ) + ∣ D 2 ∣ ∣ D ∣ Gini ( D 2 ) \operatorname{Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right)Gini(D,A)=∣D∣∣D1∣Gini(D1)+∣D∣∣D2∣Gini(D2)
4.决策树的生成。通常使用信息增益最大、信息增益比最大或基尼指数最小作为特征选择的准则。决策树的生成往往通过计算信息增益或其他指标,从根结点开 始,递归地产生决策树。这相当于用信自增益或其他准则不断地选取局部最优的特征,或将圳练集分割为能够基本正确分类的子集。
5.决策树的剪枝。由于生成的决策树存在过拟合问题,需要对它进行剪枝,以简化学到的决策树。决策树的剪枝,往往从已生成的树上剪掉一些叶结点或叶结点 以上的子树,并将其父结点或根结点作为新的叶结点,从而简化生成的决策树。
- 样本集合 ? 对特征 ? 的信息增益(ID3)
概念
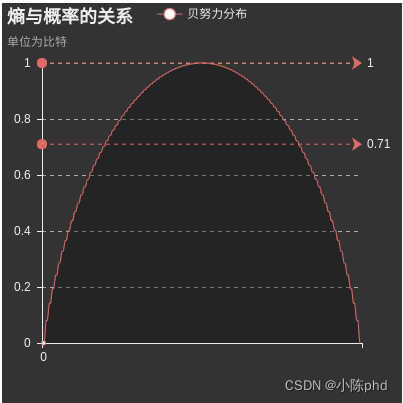
熵
H ( p ) = H ( X ) = − ∑ i = 1 n p i log p i H(p)=H(X)=-\sum_{i=1}^{n}p_i\log p_iH(p)=H(X)=−i=1∑npilogpi
熵只与X XX的分布有关,与X XX取值无关**,这句注意理解
定义0 log 0 = 0 0\log0=00log0=0,熵是非负的。
条件熵
随机变量( X , Y ) (X,Y)(X,Y)的联合概率分布为
P ( X = x i , Y = y j ) = p i j , i = 1 , 2 , … , n ; j = 1 , 2 , … , m P(X=x_i,Y=y_j)=p_{ij}, i=1,2,\dots ,n;j=1,2,\dots ,mP(X=xi,Y=yj)=pij,i=1,2,…,n;j=1,2,…,m
条件熵H ( Y ∣ X ) H(Y|X)H(Y∣X)表示在已知随机变量X XX的条件下随机变量Y YY的不确定性
H ( Y ∣ X ) = ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X)=\sum_{i=1}^np_iH(Y|X=x_i)H(Y∣X)=i=1∑npiH(Y∣X=xi)
其中p i = P ( X = x i ) , i = 1 , 2 , … , n p_i=P(X=x_i),i=1,2,\dots ,npi=P(X=xi),i=1,2,…,n
经验熵, 经验条件熵
当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时,所对应的熵与条件熵分别称为经验熵和经验条件熵
就是从已知的数据计算得到的结果。
信息增益
特征A AA对训练数据集D DD的信息增益g ( D ∣ A ) g(D|A)g(D∣A),定义为集合D DD的经验熵H ( D ) H(D)H(D)与特征A AA给定的条件下D DD的经验条件熵H ( D ∣ A ) H(D|A)H(D∣A)之差。
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A)g(D,A)=H(D)−H(D∣A)
熵与条件熵的差称为互信息.
决策树中的信息增益等价于训练数据集中的类与特征的互信息。
考虑ID这种特征, 本身是唯一的。按照ID做划分, 得到的经验条件熵为0, 会得到最大的信息增益。所以, 按照信息增益的准则来选择特征, 可能会倾向于取值比较多的特征。
g R ( D , A ) = g ( D , A ) H A ( D ) H A ( D ) = − ∑ i = 1 n D i D l o g 2 D i D g_R(D,A)=\frac{g(D,A)}{H_A(D)}\\ H_A(D)=-\sum_{i=1}^n\frac{D_i}{D}log_2\frac{D_i}{D}gR(D,A)=HA(D)g(D,A)HA(D)=−i=1∑nDDilog2DDi
算法
信息增益算法
输入:训练数据集 D DD 和特征 A AA
输出:特征 A AA 对训练数据集 D DD 的信息增益 g ( D , A ) g(D, A)g(D,A)
- 数据集 D DD 的经验樀 H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log 2 ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|}H(D)=−∑k=1K∣D∣∣Ck∣log2∣D∣∣Ck∣
- 特征 A AA 对数据集 D DD 的经验条件樀 H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 K ∣ D i k ∣ ∣ D i ∣ log 2 ∣ D i k ∣ ∣ D i ∣ H(D \mid A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \sum_{k=1}^{K} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log _{2} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|}H(D∣A)=∑i=1n∣D∣∣Di∣H(Di)=−∑i=1n∣D∣∣Di∣∑k=1K∣Di∣∣Dik∣log2∣Di∣∣Dik∣
- 信息增益 g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D, A)=H(D)-H(D \mid A)g(D,A)=H(D)−H(D∣A)
ID3算法
输入:训练数据集 D DD, 特征集 A AA ,阈值 ϵ \epsilonϵ
输出: 决策树 T TT
- 如果 D DD 属于同一类 C k , T C_{k} , TCk,T 为单节点树,类 C k C_{k}Ck 作为该节点的类标记,返回 T TT
- 如果 A AA 是空集,置 T TT 为单节点树,实例数最多的类作为该节点类标记,返回 T TT
- 计算 g gg, 选择信息增益最大的特征 A g A_{g}Ag
- 如果 A g A_{g}Ag 的信息增益小于 ϵ , T \epsilon , Tϵ,T 为单节点树, D DD 中实例数最大的类 C k C_{k}Ck 作为类标记,返回 T TT
- A g A_{g}Ag 划分若干非空子集 D i D_{i}Di ,
- D i D_{i}Di 训练集, A − A g A-A_{g}A−Ag 为特征集,递归调用前面步骤,得到 T i T_{i}Ti ,返回 T i T_{i}Ti
C4.5生成
输入:训练数据集D DD, 特征集A AA,阈值ϵ \epsilonϵ
输出:决策树T TT
- 如果D DD属于同一类C k C_kCk,T TT为单节点树,类C k C_kCk作为该节点的类标记,返回T TT
- 如果A AA是空集, 置T TT为单节点树,实例数最多的作为该节点类标记,返回T TT
- 计算g gg, 选择信息增益比最大的特征A g A_gAg
- 如果A g A_gAg的信息增益比小于ϵ \epsilonϵ,T TT为单节点树,D DD中实例数最大的类C k C_kCk作为类标记,返回T TT
- A g A_gAg划分若干非空子集D i D_iDi,
- D i D_iDi训练集,A − A g A-A_gA−Ag为特征集,递归调用前面步骤,得到T i T_iTi,返回T i T_iTi
ID3和C4.5在生成上,差异只在准则的差异。
树的剪枝
决策树损失函数摘录如下:
树T TT的叶结点个数为∣ T ∣ |T|∣T∣,t tt是树T TT的叶结点,该结点有N t N_tNt个样本点,其中k kk类的样本点有N t k N_{tk}Ntk个,H t ( T ) H_t(T)Ht(T)为叶结点t tt上的经验熵, α ⩾ 0 \alpha\geqslant 0α⩾0为参数,决策树学习的损失函数可以定义为
C α ( T ) = ∑ i = 1 ∣ T ∣ N t H t ( T ) + α ∣ T ∣ C_\alpha(T)=\sum_{i=1}^{|T|}N_tH_t(T)+\alpha|T|Cα(T)=i=1∑∣T∣NtHt(T)+α∣T∣
其中
H t ( T ) = − ∑ k N t k N t log N t k N t H_t(T)=-\sum_k\color{red}\frac{N_{tk}}{N_t}\color{black}\log \frac{N_{tk}}{N_t}Ht(T)=−k∑NtNtklogNtNtkC ( T ) = ∑ t = 1 ∣ T ∣ N t H t ( T ) = − ∑ t = 1 ∣ T ∣ ∑ k = 1 K N t k log N t k N t C(T)=\sum_{t=1}^{|T|}\color{red}N_tH_t(T)\color{black}=-\sum_{t=1}^{|T|}\sum_{k=1}^K\color{red}N_{tk}\color{black}\log\frac{N_{tk}}{N_t}C(T)=t=1∑∣T∣NtHt(T)=−t=1∑∣T∣k=1∑KNtklogNtNtk
这时有
C α ( T ) = C ( T ) + α ∣ T ∣ C_\alpha(T)=C(T)+\alpha|T|Cα(T)=C(T)+α∣T∣
其中C ( T ) C(T)C(T)表示模型对训练数据的误差,∣ T ∣ |T|∣T∣表示模型复杂度,参数α ⩾ 0 \alpha \geqslant 0α⩾0控制两者之间的影响。
上面这组公式中,注意红色部分,下面插入一个图:
这里面没有直接对H t ( T ) H_t(T)Ht(T)求和,系数N t N_tNt使得C ( T ) C(T)C(T)和∣ T ∣ |T|∣T∣的大小可比拟。这个地方再理解下。
输入:生成算法生成的整个树T TT,参数α \alphaα
输出:修剪后的子树T α T_\alphaTα
- 计算每个结点的经验熵
- 递归的从树的叶结点向上回缩
假设一组叶结点回缩到其父结点之前与之后的整体树分别是T B T_BTB和T A T_ATA,其对应的损失函数分别是C α ( T A ) C_\alpha(T_A)Cα(TA)和C α ( T B ) C_\alpha(T_B)Cα(TB),如果C α ( T A ) ⩽ C α ( T B ) C_\alpha(T_A)\leqslant C_\alpha(T_B)Cα(TA)⩽Cα(TB)则进行剪枝,即将父结点变为新的叶结点 - 返回2,直至不能继续为止,得到损失函数最小的子树T α T_\alphaTα
最小二乘回归树生成
输入:训练数据集 D DD
输出: 回归树 f ( x ) f(x)f(x)
步骤:
- 遍历变量 j jj ,对固定的切分变量 j jj 扫描切分点 s ss ,得到满足上面关系的 ( j , s ) (j, s)(j,s)
min j , s [ min c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + min c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ] \min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right]j,smin⎣⎡c1minxi∈R1(j,s)∑(yi−c1)2+c2minxi∈R2(j,s)∑(yi−c2)2⎦⎤ - 用选定的 ( j , s ) (j, s)(j,s), 划分区域并决定相应的输出值
R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } , R 2 ( j , s ) = { x ∣ x ( j ) > s } c ^ m = 1 N ∑ x i ∈ R m ( j , s ) y j , x ∈ R m , m = 1 , 2 \begin{aligned} R_{1}(j, s) &=\left\{x \mid x^{(j)} \leq s\right\}, R_{2}(j, s)=\left\{x \mid x^{(j)}>s\right\} \\ \hat{c}_{m} &=\frac{1}{N} \sum_{x_{i} \in R_{m}(j, s)} y_{j}, x \in R_{m}, m=1,2 \end{aligned}R1(j,s)c^m={x∣x(j)≤s},R2(j,s)={x∣x(j)>s}=N1xi∈Rm(j,s)∑yj,x∈Rm,m=1,2 - 对两个子区域调用(1)(2)步骤,直至满足停止条件
- 将输入空间划分为 M MM 个区域 R 1 , R 2 , … , R M R_{1}, R_{2}, \ldots, R_{M}R1,R2,…,RM ,生成决策树:
f ( x ) = ∑ m = 1 M c ^ m I ( x ∈ R m ) f(x)=\sum_{m=1}^{M} \hat{c}_{m} I\left(x \in R_{m}\right)f(x)=m=1∑Mc^mI(x∈Rm)
CART分类树生成
策略是基尼系数,所以是分类树的生成算法。
概率分布的基尼指数定义:
G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini(p) = \sum_{k=1}^Kp_k(1-p_k)=1-\sum_{k=1}^Kp_k^2Gini(p)=k=1∑Kpk(1−pk)=1−k=1∑Kpk2
基尼系数是一个来源于经济学的指标. 范围(0, 1), 有很多中表示形式, 比如衡量收入分布的基尼系数.
G = 1 n − 1 ∑ j = 1 n ( 2 j − n − 1 ) p ( i j ) G=\frac{1}{n-1}\sum_{j=1}^n(2j-n-1)p(i_j)G=n−11j=1∑n(2j−n−1)p(ij)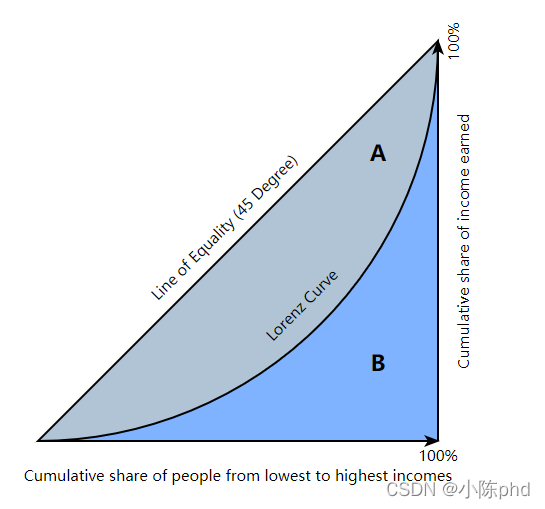
经济学基尼系数的解释,基尼系数为A A + B \frac{A}{A+B}A+BA
实现以及统计学习书上实例
def create_data():
datasets = [['青年', '否', '否', '一般', '否'],
['青年', '否', '否', '好', '否'],
['青年', '是', '否', '好', '是'],
['青年', '是', '是', '一般', '是'],
['青年', '否', '否', '一般', '否'],
['中年', '否', '否', '一般', '否'],
['中年', '否', '否', '好', '否'],
['中年', '是', '是', '好', '是'],
['中年', '否', '是', '非常好', '是'],
['中年', '否', '是', '非常好', '是'],
['老年', '否', '是', '非常好', '是'],
['老年', '否', '是', '好', '是'],
['老年', '是', '否', '好', '是'],
['老年', '是', '否', '非常好', '是'],
['老年', '否', '否', '一般', '否'],
]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
# 返回数据集和每个维度的名称
return datasets, labels
datasets, labels = create_data()
train_data = pd.DataFrame(datasets, columns=labels)
信息增益
# 定义节点类 二叉树
class Node:
def __init__(self, root=True, label=None, feature_name=None, feature=None):
self.root = root
self.label = label
self.feature_name = feature_name
self.feature = feature
self.tree = {}
self.result = {
'label:': self.label,
'feature': self.feature,
'tree': self.tree
}
def __repr__(self):
return '{}'.format(self.result)
def add_node(self, val, node):
self.tree[val] = node
def predict(self, features):
if self.root is True:
return self.label
return self.tree[features[self.feature]].predict(features)
算法实现
class DTree:
def __init__(self, epsilon=0.1):
self.epsilon = epsilon
self._tree = {}
# 熵
@staticmethod
def calc_ent(datasets):
data_length = len(datasets)
label_count = {}
for i in range(data_length):
label = datasets[i][-1]
if label not in label_count:
label_count[label] = 0
label_count[label] += 1
ent = -sum([(p / data_length) * log(p / data_length, 2)
for p in label_count.values()])
return ent
# 经验条件熵
def cond_ent(self, datasets, axis=0):
data_length = len(datasets)
feature_sets = {}
for i in range(data_length):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
cond_ent = sum([(len(p) / data_length) * self.calc_ent(p)
for p in feature_sets.values()])
return cond_ent
# 信息增益
@staticmethod
def info_gain(ent, cond_ent):
return ent - cond_ent
def info_gain_train(self, datasets):
count = len(datasets[0]) - 1
ent = self.calc_ent(datasets)
best_feature = []
for c in range(count):
c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
best_feature.append((c, c_info_gain))
# 比较大小
best_ = max(best_feature, key=lambda x: x[-1])
return best_
def train(self, train_data):
"""
input:数据集D(DataFrame格式),特征集A,阈值eta
output:决策树T
"""
_, y_train, features = train_data.iloc[:, :
-1], train_data.iloc[:,
-1], train_data.columns[:
-1]
# 1,若D中实例属于同一类Ck,则T为单节点树,并将类Ck作为结点的类标记,返回T
if len(y_train.value_counts()) == 1:
return Node(root=True, label=y_train.iloc[0])
# 2, 若A为空,则T为单节点树,将D中实例树最大的类Ck作为该节点的类标记,返回T
if len(features) == 0:
return Node(
root=True,
label=y_train.value_counts().sort_values(
ascending=False).index[0])
# 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
max_feature_name = features[max_feature]
# 4,Ag的信息增益小于阈值eta,则置T为单节点树,并将D中是实例数最大的类Ck作为该节点的类标记,返回T
if max_info_gain < self.epsilon:
return Node(
root=True,
label=y_train.value_counts().sort_values(
ascending=False).index[0])
# 5,构建Ag子集
node_tree = Node(
root=False, feature_name=max_feature_name, feature=max_feature)
feature_list = train_data[max_feature_name].value_counts().index
for f in feature_list:
sub_train_df = train_data.loc[train_data[max_feature_name] ==
f].drop([max_feature_name], axis=1)
# 6, 递归生成树
sub_tree = self.train(sub_train_df)
node_tree.add_node(f, sub_tree)
# pprint.pprint(node_tree.tree)
return node_tree
def fit(self, train_data):
self._tree = self.train(train_data)
return self._tree
def predict(self, X_test):
return self._tree.predict(X_test)
训练数据
datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)
打印树
{'label:': None, 'feature': 2, 'tree': {'否': {'label:': None, 'feature': 1, 'tree': {'否': {'label:': '否', 'feature': None, 'tree': {}}, '是': {'label:': '是', 'feature': None, 'tree': {}}}}, '是': {'label:': '是', 'feature': None, 'tree': {}}}}
链接: DataWhale.