问题:如何将一个三阶贝塞尔曲线打断生成两个三阶贝塞尔曲线,生成的两条贝塞尔曲线与原来的贝塞尔曲线重合?
输入:一条贝塞尔曲线的四个控制点P1,C1,C2,P2,和一个打断点E(E在曲线上)
输出:两条贝塞尔曲线:
P1,F,I,E
E,J,H,P2
解决大致分为两步
第一步:求出E点对应的贝塞尔曲线的参数e
第二步:根据e计算出四个控制点F,I,J,H
依次多个点打断,红色线表示原始贝塞尔,蓝色线是打断的两个贝塞尔曲线,效果如下:蓝色线和红色线基本重合。
源码
原理解析:
如图的红色曲线就是原始贝塞尔曲线,加入打断点就是E点,因为E在曲线上,所以必存在一个时刻e。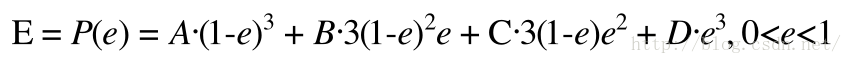
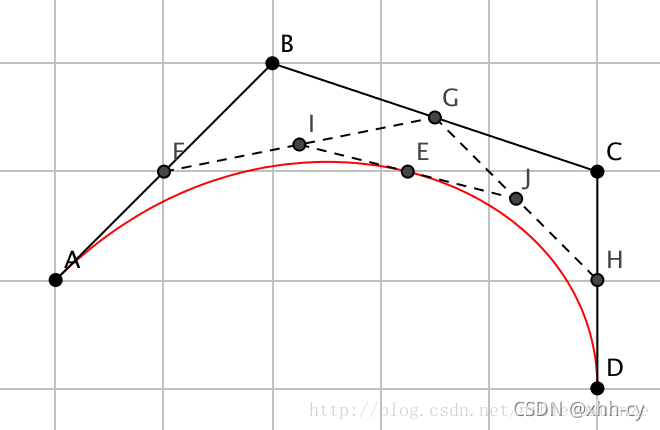
根据贝塞尔曲线的特征我们可以得到以下结论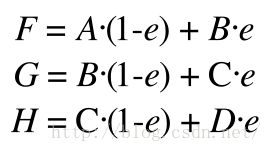
根据上式可以得到以下式子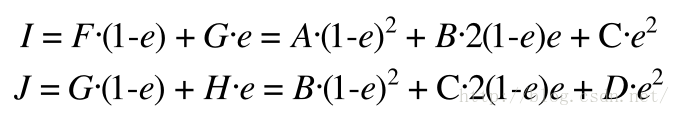
E也可以通过I和J来定义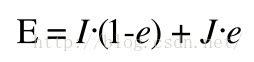
所以,如果知道断点E对应的时刻e,计算F,I,J,H相对比较简单。
下面介绍如何计算e
方法1 解方程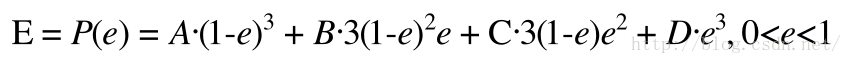
可以看到求解e就是解关于e的一元三次方程,数学相对简单,但是工程上实现较为复杂。
方法2 迭代
从0开始迭代t,设置一个步长d,计算Pi = P(ti) ti = ti+d,每次迭代时计算Pi和E的欧式距离,并记录距离最小时的时刻e = ti,就可以粗略计算出e。经测试,步长设置为0.01,效果良好。
下面给出QML代码示例:
import QtQuick 2.15
import QtQuick.Window 2.15
Window {
visible: true
width: 1920
height: 1080
title: qsTr("Hello World")
//测试点
property var testP1: Qt.vector2d(1909, 12)
property var testC1: Qt.vector2d(1910, 998)
property var testC2: Qt.vector2d(31, 15.233737999999903)
property var testP2: Qt.vector2d(11, 4)
//三次贝塞尔曲线
//a1 * (1 - t) * (1 - t) * (1 - t) + 3 * a2 * t * (1 - t) * (1 - t) + 3 * a3 * t * t * (1 - t) + a4 * t * t * t;
/*
t:时间变量 [0-1]
p1:首端点
p2:末端点
c1:首端点控制点
c2:末端点控制点
返回值:t时刻贝塞尔曲线上的点
控制点、端点和返回值的数据类型为:vector2d
*/
function thirdOrderBeziercurve(t, p1, c1, c2, p2) {
if(t<0 || t>1)
return;
var p = p1.times(Math.pow(1 - t,3))
p = p.plus(c1.times(3 * t * Math.pow(1-t,2)))
p = p.plus(c2.times(3 * (1-t) * Math.pow(t,2)))
p = p.plus(p2.times(Math.pow(t,3)))
return p
//return
}
// 计算两个点指点的距离,点的数据类型可以是vector2d或者Qt.point
function distance(p1,p2)
{
return Math.sqrt(Math.pow(p1.x-p2.x,2)+Math.pow(p1.y-p2.y,2))
}
//根据时间t获取打断后的两条贝塞尔曲线的控制点
/*
return [c11,c21,c22,c31]
*/
function getControlPointByT(p1, c1, c2, p2,t)
{
//辅助点g
var g = c1.times(1-t).plus(c2.times(t))
var c11 = p1.times(1-t).plus(c1.times(t))
var c21 = c11.times(1-t).plus(g.times(t))
var c31 = c2.times(1-t).plus(p2.times(t))
var c22 = g.times(1-t).plus(c31.times(t))
return [c11,c21,c22,c31]
}
//判断点是否在贝塞尔曲线上,如果在(误差范围内),返回时间t和逼近点
/*
输入:
p1,c1,c2,p2:是贝塞尔曲线的参数
p:特定点坐标
errorValue:误差值
输出:
1.如果p点在贝塞尔曲线上,返回打断后的两条贝塞尔曲线的控制点和纠正点[c11,c21,c22,c31,rightPoint]
2.否则,返回[]
*/
function getControlPointByPoint(p1, c1, c2, p2, p, errorValue)
{
var m = 1000000;
var t = 0
var pt = Qt.vector2d(-1,-1)
for(var i = 0;i<=1;i=i+0.01)
{
var pi = thirdOrderBeziercurve(i,p1, c1, c2, p2)
var d = distance(pi,p)
if(d< m)
{
m =d
t = i
pt = pi
}
}
if(m < errorValue)
{
console.log(t)
var ctrlsPoints = getControlPointByT(p1, c1, c2, p2,t)
//ctrlsPoints.push(pt)
return ctrlsPoints
}
return []
}
Canvas{
id:cvs
anchors.fill: parent
property var c: testP1
property var ctrs:[]
onPaint:{
var ctx = cvs.getContext('2d')
ctx.reset()
ctx.save()
ctx.clearRect(0,0,width,height)
ctx.beginPath()
ctx.moveTo(testP1.x,testP1.y)
ctx.lineWidth="4"
ctx.strokeStyle="red"
ctx.bezierCurveTo(testC1.x,testC1.y,testC2.x,testC2.y,testP2.x,testP2.y)
ctx.stroke()
//ctx.closepath()
//ctx.save()
ctx.beginPath()
ctx.arc(c.x,c.y,10,0,360,true)
ctx.stroke()
if(ctrs.length != 0)
{
ctx.lineWidth="1"
ctx.strokeStyle="blue"
ctx.beginPath()
ctx.moveTo(testP1.x,testP1.y)
ctx.bezierCurveTo(ctrs[0].x,ctrs[0].y,ctrs[1].x,ctrs[1].y,cvs.c.x,cvs.c.y)
ctx.bezierCurveTo(ctrs[2].x,ctrs[2].y,ctrs[3].x,ctrs[3].y,testP2.x,testP2.y)
ctx.stroke()
}
}
}
Timer{
interval: 100;running: true;repeat: true
property var t: 0.0
onTriggered: {
cvs.c = thirdOrderBeziercurve(t,testP1,testC1,testC2,testP2)
cvs.ctrs = getControlPointByPoint(testP1,testC1,testC2,testP2,cvs.c,100)
cvs.requestPaint()
t = t+0.01
if(t >1)
t = 0
}
}
}
版权声明:本文为GengWenhui123原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。