蓝桥杯七段码JAVA（并查集、DFS）

问题描述
小蓝要用七段码数码管来表示一种特殊的文字。
上图给出了七段码数码管的一个图示，数码管中一共有 7 段可以发光的二极管，分别标记为 a, b, c, d, e, f, g。
小蓝要选择一部分二极管（至少要有一个）发光来表达字符。
在设计字符的表达时，要求所有发光的二极管是连成一片的。
例如：b 发光，其他二极管不发光可以用来表达一种字符。
例如：c 发光，其他二极管不发光可以用来表达一种字符。
这种方案与上一行的方案可以用来表示不同的字符，尽管看上去比较相似。
例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。
例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光的二极管没有连成一片。
请问，小蓝可以用七段码数码管表达多少种不同的字符？

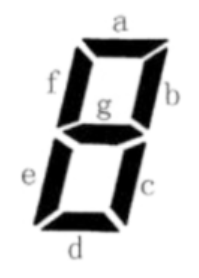
思路
abcdefg分别对应0123456
利用DFS回溯得到所有可能性
并查集判断是否连通

连通条件：
并查集的连通分量个数应该等于7个数字中没有选中的数字+1；比如选中了0124即abce，那么没有选中的个数为3，并查集的连通分量个数为5（012为一个连通分量，不出现的各自为一个连通分量，4没有与其他合并也为一个连通分量）；5不等于3+1，那么便是不连通的。

link函数含义：
先把当前要判断的选中灯的转换为set
遍历选中的灯其中每一个
如果是0，且set中有1或者5，合并；
如果是1，且set中有2或者6，合并；
如果是2，且set中有3或者6，合并；
如果是3，且set中有4，合并；
如果是4，且set中有5或者6，合并；
如果是5，且set中有6，合并；
由于取得的灯都是增序，只需要合并它之后的就可以

并查集模板

class unionfind {
	int[] parent;
	int[] size;
	int count;

	public unionfind(int n) {
		parent = new int[n];
		size = new int[n];
		count = n;
		for (int i = 0; i < n; i++) {
			parent[i] = i;
			size[i] = 1;
		}
	}
	
	public int root(int x) {
		while (x != parent[x]) {
			parent[x] = parent[parent[x]];
			x = parent[x];
		}
		return x;
	}

	//合并
	public void union(int x, int y) {
		int rootX = root(x);
		int rootY = root(y);
		if (rootX == rootY)
			return;
		if (size[rootX] < size[rootY]) {
			parent[rootX] = rootY;
			size[rootY] += size[rootX];
		} else {
			parent[rootY] = rootX;
			size[rootX] += size[rootY];
		}
		count--;
	}

}

DFS回溯求得所有子序列模板

//deque用于保存子序列 这里可以改成各种需要回溯的数据结构
public void dfs(List<List<Integer>> list,ArrayDeque<Integer> deque,int begin)
	{
		if(//终止条件)
		{
			return;
		}
		list.add(new ArrayList(deque));//保存数据
		for (; begin<//数组长度; begin++) {
			deque.addLast(begin);
			dfs(list,deque,begin+1);
			deque.pollLast();
		}
	}

二者结合

class unionfind {
	int[] parent;
	int[] size;
	int count;

	public unionfind(int n) {
		parent = new int[n];
		size = new int[n];
		count = n;
		for (int i = 0; i < n; i++) {
			parent[i] = i;
			size[i] = 1;
		}
	}

	public int root(int x) {
		while (x != parent[x]) {
			parent[x] = parent[parent[x]];
			x = parent[x];
		}
		return x;
	}

	public void union(int x, int y) {
		int rootX = root(x);
		int rootY = root(y);
		if (rootX == rootY)
			return;
		if (size[rootX] < size[rootY]) {
			parent[rootX] = rootY;
			size[rootY] += size[rootX];
		} else {
			parent[rootY] = rootX;
			size[rootX] += size[rootY];
		}
		count--;
	}

}


public class Main {
	public static void main(String[] args) {
		List<List<Integer>> numlist = new ArrayList<>();
		ArrayDeque<Integer> deque = new ArrayDeque();
		dfs(numlist,deque,0);
		List<List<Integer>> listres = new ArrayList();
		for (int i = 1; i < numlist.size(); i++) {
			List<Integer> getlist = numlist.get(i);
			if(link(getlist))
			{
				listres.add(getlist);
			}
		}
		System.out.println(listres.size());
	}
	
	public static void dfs(List<List<Integer>> numlist,ArrayDeque<Integer> deque,int begin)
	{
		if(begin>7)
		{
			return;
		}
		numlist.add(new ArrayList(deque));
		for (; begin <7; begin++) {
			deque.addLast(begin);
			dfs(numlist,deque,begin+1);
			deque.pollLast();
		}
	}
	
	public static boolean link(List<Integer> getlist) {
		Set<Integer> set = new HashSet(getlist);
		unionfind uf = new unionfind(7);
		for (int i = 0; i < getlist.size(); i++) {
			if(getlist.get(i)==0)
			{
				if(set.contains(1))
				{
					uf.union(0, 1);
				}
				if(set.contains(5))
				{
					uf.union(0,5);
				}
			}
			if(getlist.get(i)==1)
			{
				if(set.contains(2))
				{
					uf.union(1, 2);
				}
				if(set.contains(6))
				{
					uf.union(1,6);
				}
			}
			if(getlist.get(i)==2)
			{
				if(set.contains(3))
				{
					uf.union(2, 3);
				}
				if(set.contains(6))
				{
					uf.union(2,6);
				}
			}
			if(getlist.get(i)==3)
			{
				if(set.contains(4))
				{
					uf.union(3, 4);
				}
			}
			if(getlist.get(i)==4)
			{
				if(set.contains(5))
				{
					uf.union(4, 5);
				}
				if(set.contains(6))
				{
					uf.union(4,6);
				}
			}
			if(getlist.get(i)==5)
			{
				if(set.contains(6))
				{
					uf.union(5, 6);
				}
			}
		}
		return 7-getlist.size()+1==uf.count;
	}
}