简述一下线性回归流程:首先可以进行数据的预处理,包括但不限于:缺失值处理、线性相关的特征值处理、误差较大的脏数据处理。然后搭建一个线性回归模型,运用梯度下降或者正规方程法可以求出参数,这样模型就确定了。之后再用一些检测方法,评估模型是否合理并进行针对性的优化。
文中y ^ \hat{y}y^为预测值,y ( i ) y^{(i)}y(i)为实际值,x i x_{i}xi表示第i ii个变量(特征),x ( i ) x^{(i)}x(i)表示第i ii组数据(样本),同理x n ( m ) x_{n}^{(m)}xn(m)表示第m个样本的第n个特征
第1.2章:线性回归参数的求解
来源
本章视频
06_线性回归算法原理推导、07_线性回归参数的求解
一、线性回归算法原理推导
二、线性回归参数的求解(求函数最小值)
1.正规方程法
将目标函数(04)转化为矩阵形式可以简化推导过程,有利于代码实现:J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 ( X θ − Y ) T ( X θ − Y ) ( 06 ) J(\theta)=\frac{1}{2} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}=\frac{1}{2}(X \theta-Y)^{T}(X \theta-Y) (06)J(θ)=21i=1∑m(hθ(x(i))−y(i))2=21(Xθ−Y)T(Xθ−Y)(06) 其中X = [ x 0 ( 1 ) x 1 ( 1 ) ⋯ x n ( 1 ) x 0 ( 2 ) x 1 ( 2 ) ⋯ x n ( 2 ) ⋯ ⋯ ⋯ ⋯ x 0 ( m ) x 1 ( m ) ⋯ x n ( m ) ] = [ 1 x 1 ( 1 ) ⋯ x n ( 1 ) 1 x 1 ( 2 ) ⋯ x n ( 2 ) ⋯ ⋯ ⋯ ⋯ 1 x 1 ( m ) ⋯ x n ( m ) ] \mathbf{X} = \left[\begin{array}{cccc}{x_{0}^{(1)}} & {x_{1}^{(1)}} & {\cdots} & {x_{n}^{(1)}} \\ {x_{0}^{(2)}} & {x_{1}^{(2)}} & {\cdots} & {x_{n}^{(2)}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {x_{0}^{(m)}} & {x_{1}^{(m)}} & {\cdots} & {x_{n}^{(m)}}\end{array}\right] = \left[\begin{array}{cccc}{1} & {x_{1}^{(1)}} & {\cdots} & {x_{n}^{(1)}} \\ {1} & {x_{1}^{(2)}} & {\cdots} & {x_{n}^{(2)}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {1} & {x_{1}^{(m)}} & {\cdots} & {x_{n}^{(m)}}\end{array}\right]X=⎣⎢⎢⎢⎡x0(1)x0(2)⋯x0(m)x1(1)x1(2)⋯x1(m)⋯⋯⋯⋯xn(1)xn(2)⋯xn(m)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡11⋯1x1(1)x1(2)⋯x1(m)⋯⋯⋯⋯xn(1)xn(2)⋯xn(m)⎦⎥⎥⎥⎤ , θ = [ θ 0 θ 1 ⋯ θ n ] \theta=\left[\begin{array}{l}{\theta_{0}} \\ {\theta_{1}} \\ {\cdots} \\ {\theta_{n}}\end{array}\right]θ=⎣⎢⎢⎡θ0θ1⋯θn⎦⎥⎥⎤ , Y = [ y ( 1 ) y ( 2 ) ⋯ y ( m ) ] Y=\left[\begin{array}{l}{y^{(1)}} \\ {y^{(2)}} \\{\cdots} \\ {y^{(m)}}\end{array}\right]Y=⎣⎢⎢⎡y(1)y(2)⋯y(m)⎦⎥⎥⎤
现在问题转化为求目标函数的极小值点,只要令d J ( θ ) d θ \frac{\mathrm{d} \mathrm{J}(\theta)}{\mathrm{d} \theta}dθdJ(θ)=0即可解出θ \thetaθ的值,目标函数J ( θ ) J(\theta)J(θ)对θ \thetaθ求导得:∇ θ J ( θ ) = ∇ θ ( 1 2 ( X θ − Y ) T ( X θ − Y ) ) = ∇ θ ( 1 2 ( θ T X T − Y T ) ( X θ − Y ) ) \nabla_{\theta} J(\theta)=\nabla_{\theta}\left(\frac{1}{2}(X \theta-Y)^{T}(X \theta-Y)\right)=\nabla_{\theta}\left(\frac{1}{2}\left(\theta^{T} X^{T}-Y^{T}\right)(X \theta-Y)\right)∇θJ(θ)=∇θ(21(Xθ−Y)T(Xθ−Y))=∇θ(21(θTXT−YT)(Xθ−Y))= ∇ θ ( 1 2 ( θ T X T X θ − θ T X T Y − Y T X θ + Y T Y ) ) =\nabla_{\theta}\left(\frac{1}{2}\left(\theta^{T} X^{T} X \theta-\theta^{T} X^{T} Y-Y^{T} X \theta+Y^{T} Y\right)\right)=∇θ(21(θTXTXθ−θTXTY−YTXθ+YTY))= 1 2 ( 2 X T X θ − X T Y − ( Y T X ) T ) = X T X θ − X T Y ( 07 ) =\frac{1}{2}\left(2 X^{T} X \theta-X^{T} Y-\left(Y^{T} X\right)^{T}\right)=X^{T} X \theta-X^{T} Y (07)=21(2XTXθ−XTY−(YTX)T)=XTXθ−XTY(07)结果是一个( n + 1 ) ∗ 1 (n+1) * 1(n+1)∗1的向量,形似[ Z 0 ⋮ Z n ] \left[\begin{array}{c}{Z_{0}} \\ {\vdots} \\ {Z_{n}}\end{array}\right]⎣⎢⎡Z0⋮Zn⎦⎥⎤
令(05)式为0,得最终参数值:θ = ( X T X ) − 1 X T Y ( 08 ) \theta=\left(X^{T} X\right)^{-1} X^{T} Y (08)θ=(XTX)−1XTY(08)
关于正规方程法的几点说明:
- 对于那些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征,也有可能是特征数量大于训练集的数量),正规方程方法是不能用的。也就是说,只有矩阵( X T X ) \left(X^{T} X\right)(XTX)是可逆矩阵的时候,这个方法才可行。矩阵可逆=矩阵对应的行列式不为0=满秩=行(列)向量线性无关
- 如果特征数量n nn较大则运算代价大,因为矩阵逆的计算时间复杂度为O ( n 3 ) O\left(n^{3}\right)O(n3),通常来说当n nn小于100时还是可以接受的
- 只适用于线性模型,不适合逻辑回归模型等其他模型。事实上对于那些更复杂的学习算法,我们将不得不仍然使用梯度下降法,但对于这个特定的线性回归模型,正规方程法是一个比梯度下降法更快的替代算法。
- 关于矩阵求导术
2.梯度下降法
正规方程法并不是什么情况都能奏效的,事实上大多数复杂算法都不适用。而梯度下降法作为一种求函数最小值更加通用的手段,适用的范围更广,操作方法也更符合机器学习的理念(让机器循着特定的算法程序进行迭代运行)。梯度的方向是函数值变化最快的方向,如果是求极大值,沿着梯度的方向迭代即可;如果是求极小值,则沿着梯度相反的方向迭代
- 【补充一点个人理解】为什么要用梯度来进行参数的更新?当只有一个参数θ \thetaθ时,初始化以后,下一步θ \thetaθ是变大还是变小呢?我们用导数就可以很好的回答这个问题,当这个点导数为正时,增大θ \thetaθ的值则函数值(这里是损失函数)增加,减小θ \thetaθ则函数值减小。所以梯度充当的就是一个方向的作用,它指导参数θ \thetaθ的变化方向,在这个时候梯度的大小不是非常重要,因为更新参数θ \thetaθ时还要乘上步长,可以通过调整步长来控制更新的幅度。当参数θ \thetaθ是一个向量时( θ 0 , θ 1 , … , θ n ) \left(\theta_{0}, \theta_{1}, \ldots, \theta_{n}\right)(θ0,θ1,…,θn),也是类似的,梯度代表的是向量的方向,是兼顾了各个参数方向最终得出来的,也可以认为一次性更新θ 0 , θ 1 , … , θ n \theta_{0}, \theta_{1}, \ldots, \theta_{n}θ0,θ1,…,θn,幅度由步长来控制。
梯度下降背后的思想
- 开始时我们随机选择一个参数的组合( θ 0 , θ 1 , … , θ n ) \left(\theta_{0}, \theta_{1}, \ldots, \theta_{n}\right)(θ0,θ1,…,θn),计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。
- 我们持续这么做直到得到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。
- Repeat { θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 , … , θ n ) } \begin{array}{l}{\text { Repeat }\{ } \\ {\qquad \theta_{j} :=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}, \ldots, \theta_{n}\right)} \\ {\}}\end{array} Repeat {θj:=θj−α∂θj∂J(θ0,θ1,…,θn)}
梯度下降的迭代方法
1.代数法
构建一个代价函数(参照(05)式):J ( θ 0 , θ 1 … θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 , 其 中 h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + … + θ n x n , x 0 = 1 J\left(\theta_{0}, \theta_{1} \ldots \theta_{n}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2},其中h_{\theta}(x)=\theta_{0} x_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{n} x_{n},x_{0}=1J(θ0,θ1…θn)=2m1i=1∑m(hθ(x(i))−y(i))2,其中hθ(x)=θ0x0+θ1x1+θ2x2+…+θnxn,x0=1 ∂ ∂ θ j J ( θ 0 , θ 1 , … , θ n ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) , 导 数 可 能 是 正 的 也 可 能 是 负 的 , 取 决 于 切 线 的 斜 率 \frac{\partial}{\partial \theta_{j}} \mathrm{J}\left(\theta_{0}, \theta_{1}, \ldots, \theta_{\mathrm{n}}\right)=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)},导数可能是正的也可能是负的,取决于切线的斜率∂θj∂J(θ0,θ1,…,θn)=m1i=1∑m(hθ(x(i))−y(i))xj(i),导数可能是正的也可能是负的,取决于切线的斜率
重复迭代:θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 , … , θ n ) , 其 中 j = 0 , 1 , . . . , n \theta_{j} :=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} \mathrm{J}\left(\theta_{0}, \theta_{1}, \ldots, \theta_{\mathrm{n}}\right),其中j=0,1,...,nθj:=θj−α∂θj∂J(θ0,θ1,…,θn),其中j=0,1,...,n即 θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ( 09 ) 即\theta_{j} :=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} (09)即θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)(09)
2.矩阵法
构建一个代价函数(参照(06)式):J ( θ ) = 1 2 m ( X θ − Y ) T ( X θ − Y ) , ∇ θ J ( θ ) = 1 m ( X T X θ − X T Y ) J(\theta)=\frac{1}{2m}(X \theta-Y)^{T}(X \theta-Y),\nabla_{\theta} J(\theta)=\frac{1}{m}(X^{T} X \theta-X^{T} Y)J(θ)=2m1(Xθ−Y)T(Xθ−Y),∇θJ(θ)=m1(XTXθ−XTY)
重复迭代:θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 , … , θ n ) , 其 中 j = 0 , 1 , . . . , n \theta_{j} :=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} \mathrm{J}\left(\theta_{0}, \theta_{1}, \ldots, \theta_{\mathrm{n}}\right),其中j=0,1,...,nθj:=θj−α∂θj∂J(θ0,θ1,…,θn),其中j=0,1,...,n即 θ : = θ − α 1 m ( X T X θ − X T Y ) ( 10 ) 即\theta :=\theta-\alpha\frac{1}{m}\left(X^{T} X \theta-X^{T} Y\right) (10)即θ:=θ−αm1(XTXθ−XTY)(10)
3.几点补充
- α \alphaα取正数,以凸函数为例(形如y = x 2 y=x^{2}y=x2):当θ j \theta_{j}θj位于极小值点右侧,导数大于0,更新后θ j \theta_{j}θj向左移动;当θ j \theta_{j}θj位于极小值点左侧,导数小于0,更新后θ j \theta_{j}θj向右移动。同理,若是凹函数,则会远离极大值点。也就是说,在学习率a的大小选取合适的情况下,θ j \theta_{j}θj越来越靠近极小值点,随着迭代次数不断增加,函数值在极小值点左右晃动。
- 对θ \thetaθ的更新方式一般采用同时更新,即采用老的一组( θ 0 , θ 1 , … , θ n ) \left(\theta_{0}, \theta_{1}, \ldots, \theta_{n}\right)(θ0,θ1,…,θn)来更新θ j \theta_{j}θj,也就是说更新θ 1 \theta_{1}θ1的时候,θ 0 \theta_{0}θ0还是那个没有更新的θ 0 \theta_{0}θ0。其实矩阵法就很能说明过程
- 不适用于非光滑函数,即某些位置的导数可能不存在
梯度下降的参数选取
1.初始参数
- 初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值
- 由于有局部最优解的风险,需要多次用不同初始值运行算法,比较这些局部最优解,选择使目标函数最小的值
2.学习率(步长)
- α \alphaα是学习率(learning rate),它决定了我们让代价函数下降的步子有多大。如果α \alphaα选取太小,它会需要很多步才能到达最低点。如果α \alphaα选取的太大,它会导致无法收敛甚至发散。可以考虑尝试这些学习率:α \alphaα=0.001,0.003,0.01,0.03,0.1,0.3,1…每两个取值大概相差三倍,起始位置可以考虑α \alphaα=0.01
- 之所以让代价函数除以一个样本数m mm,就是考虑对于不同的模型来说样本数可能是100也可能是100万,为了使每次取的α \alphaα变化不会太过剧烈(让人对起始位置无从下手),于是对误差的求和除以一个m mm,这样每次都可以用α \alphaα=0.01来开始尝试
- 当我们接近局部最低时,导数值会自动变得越来越小,所以梯度下降将自动采取较小的幅度,因此实际上没有必要再另外减小α \alphaα,当然非要进行减小也是可以的
3.特征缩放
- 在我们面对多维特征问题的时候,我们要尽量使这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
- 以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000平方英尺,而房间数量的值则是0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图,则图像会显得扁长,梯度下降算法需要非常多次的迭代才能收敛,而我们理想的等高线图尽量是圆形的好。解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间(-1/3到1/3,-3到3都可以)
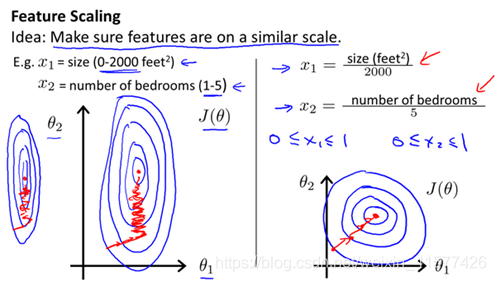
- 另一种可行的方法是令:x i = x i − μ n s n x_{i}=\frac{x_{i}-\mu_{n}}{s_{n}}xi=snxi−μn,其中μ n \mu_{n}μn是平均值,S n S_{n}Sn是标准差(用最大值减最小值就可以了)。特征缩放不需要太精确,主要是让梯度下降算法运行的能够更快一些。
4.终止条件
可以通过绘制“迭代次数”和“代价函数的值”的图,来观测算法在何时趋于收敛
一种方法是:定义一个合理的阈值如0.001,当两次迭代之间J ( θ ) J(\theta)J(θ)的差值小于该阈值时,迭代结束。
或者设置一个大概的迭代步数,比如1000或500,梯度下降法最终的迭代肯定会收敛,只要达到相应迭代次数,多了也没关系。
5.其他模型转化为线性模型
- 有时对于一批数据,线性模型不一定是最好的拟合方式,可能需要曲线来适应我们的数据,比如一个二次方模型:h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}^{2}hθ(x)=θ0+θ1x1+θ2x22,或者三次方模型:h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 + θ 3 x 3 3 h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}^{2}+\theta_{3} x_{3}^{3}hθ(x)=θ0+θ1x1+θ2x22+θ3x33
- 此时,我们可以令:x 2 = x 1 2 , x 3 = x 1 3 x_{2}=x_{1}^{2}, x_{3}=x_{1}^{3}x2=x12,x3=x13,从而将模型转化为线性回归模型。
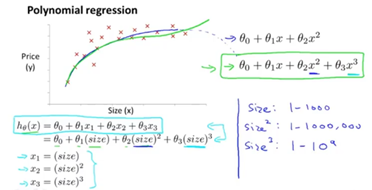
- 根据函数图形特性,我们还可以使:h θ ( x ) = θ 0 + θ 1 ( s i z e ) + θ 2 siz e h_{\theta}(x)=\theta_{0}+\theta_{1}(s i z e)+\theta_{2} \sqrt{\operatorname{siz} e}hθ(x)=θ0+θ1(size)+θ2size
3.梯度下降法家族
批量梯度下降
- 上文所提到的就是批量梯度下降(Batch Gradient Descent),这是梯度下降法最基本的形式,具体做法就是在更新参数θ \thetaθ时用上所有的m mm个样本。
- 优点是计算得精度比较高,容易得到最优解。
- 缺点是由于样本数量太大,计算速度很慢。
随机梯度下降
- 随机梯度下降(Stochastic Gradient Descent),在更新参数θ \thetaθ时没有用所有的m个样本的数据,而是随机选取一个样本i ii来求梯度:θ j : = θ j − α ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) , 其 中 j = 0 , 1 , . . . , n ( 11 ) \theta_{j} :=\theta_{j}-\alpha \left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)},其中j=0,1,...,n (11)θj:=θj−α(hθ(x(i))−y(i))xj(i),其中j=0,1,...,n(11)
- 优点:相比于批量梯度下降,随机梯度下降只选取了一个样本,因此迭代速度提升了很多
- 缺点:由于随机梯度下降法每次迭代只选择一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。如果选择的样本属于一个误差比较大的脏数据,前进的方向都不一定是收敛方向。
小批量梯度下降
- 小批量梯度下降(Mini-batch Gradient Descent),是批量梯度下降法和随机梯度下降法的折衷。也就是对于m个样本,我们选取其中的x xx个样本来迭代,1 < x < m 1<x<m1<x<m,即:θ j : = θ j − α 1 x ∑ i = t x + t − 1 ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) , 其 中 j = 0 , 1 , . . . , n ( 12 ) \theta_{j} :=\theta_{j}-\alpha \frac{1}{x} \sum_{i=t}^{x+t-1}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} ,其中j=0,1,...,n (12)θj:=θj−αx1i=t∑x+t−1(hθ(x(i))−y(i))xj(i),其中j=0,1,...,n(12)
- 这个算法每次选择一部分数据更新,在实际操作中是最实用的。每次选择的样本数x xx可以是32、64、128,差不多选择64就可以了,具体取决于你能容忍算法运行多久,选择的越多则精度越高。