一. 自注意力机制之位置编码

1. 位置编码

在处理词元序列时，循环神经网络是逐个的重复地处理词元的，而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息，我们通过在输入表示中添加位置编码（positional encoding）来注入绝对的或相对的位置信息。位置编码可以通过学习得到也可以直接固定得到。下面使用基于正弦函数和余弦函数的固定位置编码：
假设输入表示 $\mathbf{X} \in \mathbb{R}^{n \times d}$ 包含一个序列中 $n$ 个词元的 $d$ 维嵌入表示。位置编码使用相同形状的位置嵌入矩阵 $\mathbf{P} \in \mathbb{R}^{n \times d}$ 输出 $\mathbf{X} + \mathbf{P}$ ，矩阵第 $i$ 行、第 $2 j$ 列和 $2 j + 1$ 列上的元素为：

$\begin{aligned} p_{i, 2j} &= \sin\left(\frac{i}{10000^{2j/d}}\right),\\p_{i, 2j+1} &= \cos\left(\frac{i}{10000^{2j/d}}\right).\end{aligned}$

2. 位置编码实现

import torch
import d2l.torch
from torch import nn
class PositionalEncoding(nn.Module):
    """位置编码"""
    def __init__(self,num_hiddens,dropout,max_len=1000):
        super(PositionalEncoding,self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P
        self.P = torch.zeros(size=(1,max_len,num_hiddens))
        X = torch.arange(max_len,dtype=torch.float32).reshape(-1,1)/torch.pow(1000,torch.arange(0,num_hiddens,2,dtype=torch.float32)/num_hiddens)
        self.P[:,:,0::2] = torch.sin(X)
        self.P[:,:,1::2] = torch.cos(X)
    def forward(self,X):
        X = X+self.P[:,:X.shape[1],:].to(X.device)
        return self.dropout(X)

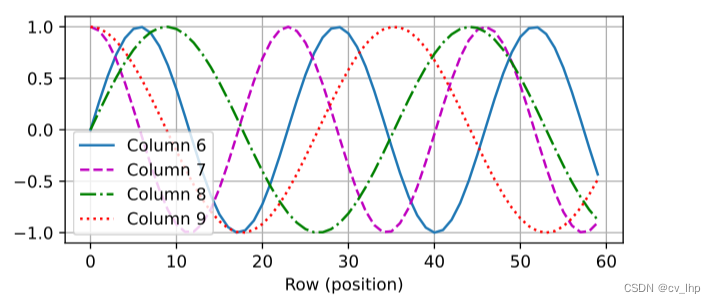
在位置嵌入矩阵 ? 中，行代表词元在序列中的位置，列代表不同维度的位置编码。如下面图所示我们可以看到位置嵌入矩阵的第 6 列和第 7 列的频率高于第 8 列和第 9 列。第 6 列和第 7 列之间的偏移量（第 8 列和第 9 列相同）是由于正弦函数和余弦函数的交替。

encoding_dim,num_steps = 32,60
pos_encoding = PositionalEncoding(encoding_dim,0)
pos_encoding.eval()
X = pos_encoding(torch.zeros(size=(1,num_steps,encoding_dim)))
P = pos_encoding.P[:,:X.shape[1],:]
d2l.torch.plot(torch.arange(num_steps),Y=P[0,:,6:10].T,xlabel='Row (position)',figsize=(6,2.5),legend=['Column %d' %d for d in torch.arange(6,10)])

位置编码数值的可视化
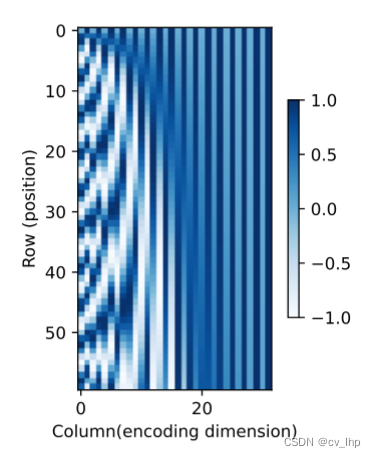
使用热力图显示每一个样本序列的位置编码：

P = P[0,:,:].unsqueeze(0).unsqueeze(0)
d2l.torch.show_heatmaps(P,xlabel='Column(encoding dimension)',ylabel='Row (position)',figsize=(3.5,4),cmap='Blues')

热力图显示每一个样本序列的位置编码

3. 相对位置信息

除了捕获绝对位置信息之外，上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移 $\delta$ ，位置 $\delta$ 处的位置编码可以线性投影位置 $i$ 处的位置编码来表示。这种投影的数学解释是，令 $\omega_j = 1/10000^{2j/d}$ ，对于任何确定的位置偏移 $\delta$ ，任何一对 $p_{i, 2j}, p_{i, 2j+1})$ 都可以线性投影到 $(p_{i+\delta, 2j}, p_{i+\delta, 2j+1})$ ：

$\begin{aligned} &\begin{bmatrix} \cos(\delta \omega_j) & \sin(\delta \omega_j) \\ -\sin(\delta \omega_j) & \cos(\delta \omega_j) \\ \end{bmatrix} \begin{bmatrix} p_{i, 2j} \\ p_{i, 2j+1} \\ \end{bmatrix}\\ =&\begin{bmatrix} \cos(\delta \omega_j) \sin(i \omega_j) + \sin(\delta \omega_j) \cos(i \omega_j) \\ -\sin(\delta \omega_j) \sin(i \omega_j) + \cos(\delta \omega_j) \cos(i \omega_j) \\ \end{bmatrix}\\ =&\begin{bmatrix} \sin\left((i+\delta) \omega_j\right) \\ \cos\left((i+\delta) \omega_j\right) \\ \end{bmatrix}\\ =& \begin{bmatrix} p_{i+\delta, 2j} \\ p_{i+\delta, 2j+1} \\ \end{bmatrix}, \end{aligned}$

$2\times 2$ 投影矩阵不依赖于任何位置的索引 $i$ 。

4. 小结

为了使用序列的顺序信息，可以通过在输入表示中添加位置编码，来注入绝对的或相对的位置信息。

5. 全部代码

import torch
import d2l.torch
from torch import nn


class PositionalEncoding(nn.Module):
    """位置编码"""

    def __init__(self, num_hiddens, dropout, max_len=1000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P
        self.P = torch.zeros(size=(1, max_len, num_hiddens))
        X = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1) / torch.pow(1000, torch.arange(0, num_hiddens, 2,
                                                                                                     dtype=torch.float32) / num_hiddens)
        self.P[:, :, 0::2] = torch.sin(X)
        self.P[:, :, 1::2] = torch.cos(X)

    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)


encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros(size=(1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.torch.plot(torch.arange(num_steps), Y=P[0, :, 6:10].T, xlabel='Row (position)', figsize=(6, 2.5),
               legend=['Column %d' % d for d in torch.arange(6, 10)])
P = P[0, :, :].unsqueeze(0).unsqueeze(0)
d2l.torch.show_heatmaps(P, xlabel='Column(encoding dimension)', ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')

原文链接：https://blog.csdn.net/flyingluohaipeng/article/details/125786973

李沐动手学深度学习V2-自注意力机制之位置编码