交集运算

背景

当我在公司做打包业务时，经常会遇到这样的场景：新打包的组合要和数据库里存在的组合对比，然后把公共的部分提取出来。这里就涉及到求两个集合的交集运算。

思路演进

1.暴力算法

当时想的是用的是set的contain方法，交集即左边有元素包含在右面，代码如下

   public static Set<String> operIntersect(Set<String> leftSet , Set<String> rightSet){
        Set<String> intersectSet=new HashSet<String>();
        Iterator<String> it=leftSet.iterator();
        while(it.hasNext()){
            String e=it.next();
            if(rightSet.contains(e)){
                intersectSet.add(e);
            }
        }
        return intersectSet;
    }

set的contains查找是线性查找，整个实现的复杂度o（n2），效率有点低下

2.排序法

先排序，然后在一个个比,如下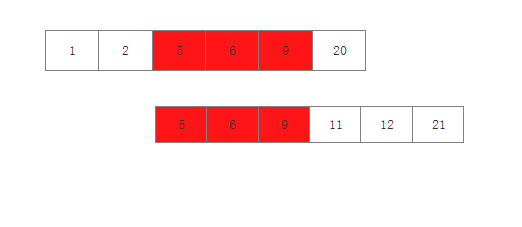

代码如下：

 /**
     * 求交集
     * @param leftMap
     * @param rightMap
     * @return
     */
    public static <T>List<Long> getIntersection(Map<Long, T> leftMap, Map<Long, T> rightMap) {
        Long[] la = leftMap.keySet().toArray(new Long[leftMap.size()]);
        Long[] ra = rightMap.keySet().toArray(new Long[rightMap.size()]);
        // 先排序
        Arrays.sort(la);
        Arrays.sort(ra);
        List<Long> swapList = new ArrayList<Long>();
        // o(n)求交集
        for (int i = 0, j = 0; i < la.length && j < ra.length;) {
            if (la[i] == ra[j]) {
                swapList.add(la[i]);
                i++;
                j++;
            } else {
                if (la[i] < ra[j])
                    i++;
                else
                    j++;
            }
        }
        return swapList;
    }

这种求交集的算法时间复杂度浪费在了排序上，此处用的Arrays.sort 归并排序O(n*logn)，总的时间复杂度O(n*logn)+O(n)

3.hash计数法

后来我在做套餐时间价格表的时候，又遇到了另外的一个应用场景，需要求得在一个时间段内，套餐下包含的酒店，交通，线路的日期交集,也就是多个日期的集合，求他们的交集。排序法显然不适用这里的场景
* 空间换时间：遍历所有的元素，用hash表统计每个元素出现的次数 。
所谓的交集就是元素出现次数==可变长集合数组的长度.
* 代码如下

/**
     * 求多个set数组的交集
     * @param setArrays
     * @return
     */
    public static <String> Set<String> operInsertct(Set<String>... setArrays) {
        // 计数map
        Map<String, Integer> countMap = new HashMap<String, Integer>();
        for (int i = 0; i < setArrays.length; i++) {
            for (String element : setArrays[i]) {
                Integer keyCount = (Integer) countMap.get(element);
                if (keyCount == null) {
                    countMap.put(element, 1);
                } else {
                    countMap.put(element, ++keyCount);
                }
            }
        }
        //元素出现setArrays.length代表元素在交集
        Iterator<Entry<String, Integer>> iterator = countMap.entrySet().iterator();
        while (iterator.hasNext()) {
            if ((Integer) iterator.next().getValue() != setArrays.length) {
                iterator.remove();
            }
        }
        return countMap.keySet();
    }

时间复杂度O(N)
空间复杂度O(2N)

4.拓展

hash计数法实际上得益于计数排序的思想