排序算法是程序中常用的算法,今天我整理了一些常用的算法,供大家学习使用。
首先我们来看一长这样的图集,包含了大多数的排序方法

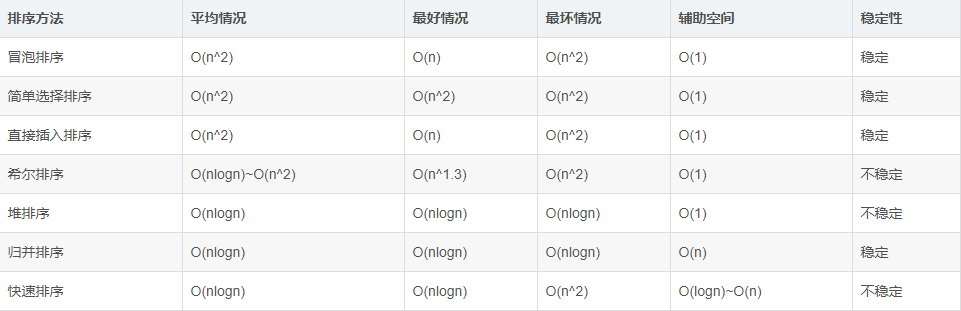
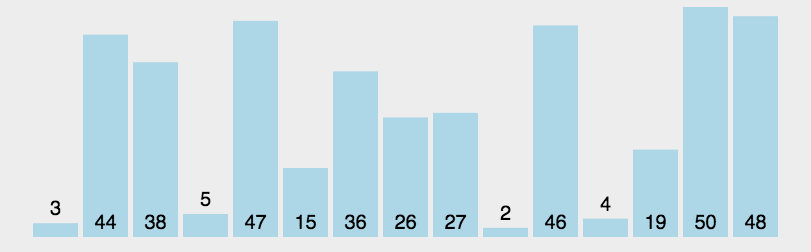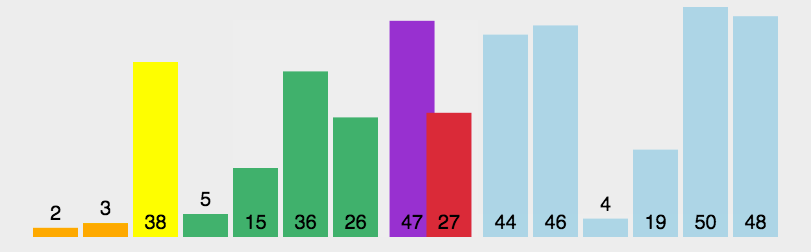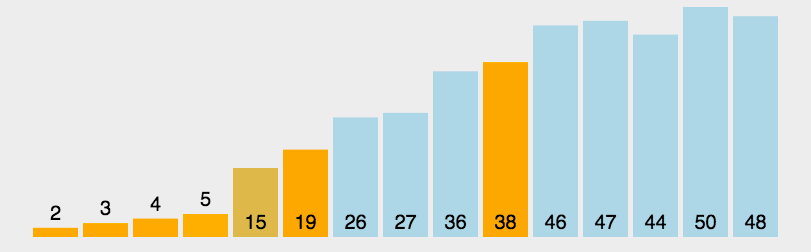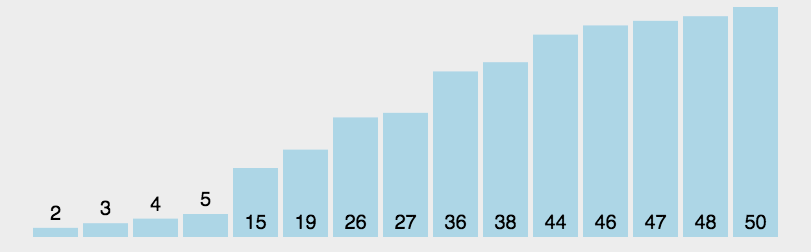
各种排序的时间复杂度
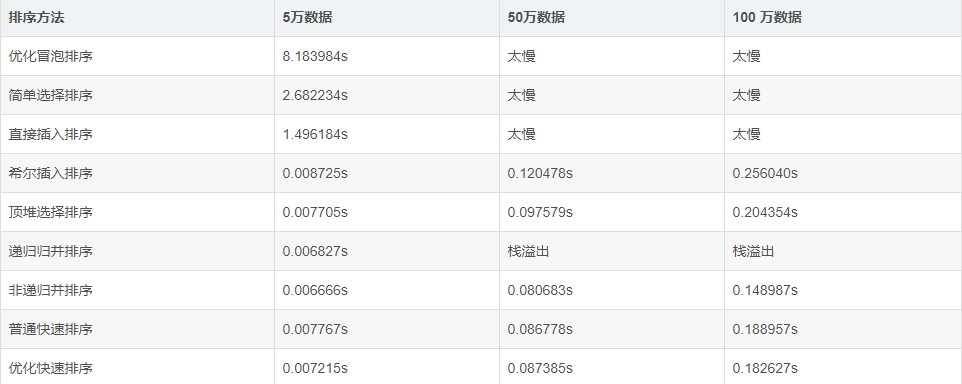
各种排序的时间测试
1.冒泡排序
- 与相邻位置进行比较,依次浮出最大或最小的值。
- 优化方案,可以增加标记位,已经有序的不用再冒泡。
实现代码:
int BubbleSort1(SqList * L)
{
int i, j;
int flag = 1;
for (i = 0; i < MAXSIZE - 1 && flag; i++) {
flag = 0; // 若标志位flag不为1,说明已经有序,这个时候就可以退出循环了
for (j = MAXSIZE - 1; j > i; j--) {
if (L->r[j] < L->r[j - 1]) {
swap(L, j, j - 1);
flag = 1;
}
}
}
return 0;
}2.简单选择排序
- 通过n-i次关键字之间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i个记录作交换
代码实现:
void SelectSort(int*a, int length) {
int min;
int i, j;
for (i = 0; i < length - 1; ++i) {
min = i;
for (j = i + 1; j < length; ++j) {
if (a[min] > a[j]) {
min = j;
}
}
if (i != min) {
T tmp;
tmp = a[min];
a[min] = a[i];
a[i] = tmp;
}
}
}3.插入排序
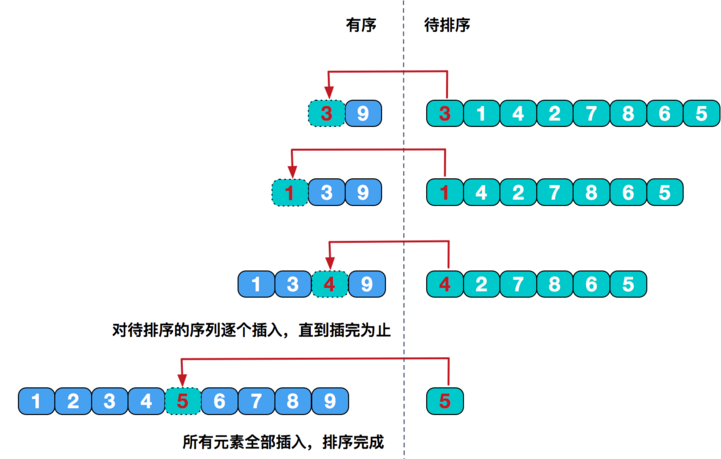
- 将待排序的一组序列分为已排好序和未排好序的两个部分
- 初始状态时,已排好序序列仅包含第一个元素,未排好序的序列元素为除去第一个以外的n-1个元素
- 然后,将未排好序序列中的元素逐一插入到已排好序的序列中
- 如此往复,经过n-1次插入后,未排序序列中的元素个数变为0,排序完成。如下图所示
代码实现:
void InsterSort(int*a, int length) {
int temp;
int i, j;
for (i = 1; i < length ; ++i) {
min = i;
for (j = i ; j > 0&&a[j-1]>temp; --j) {
a[j]=a[j-1];
}
a[j] = temp;
}
}4.希尔排序
- 希尔排序是插入排序的一种高效率的实现,也叫缩小增量排序。先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录基本有序时再对全体记录进行一次直接插入排序。
- 关于增量取法,没有统一标准,但最后一步必须是1;因为不同的取法涉及时间复杂度不一样,具体了解可以参考《数据结构与算法分析》;一般以length/2为算法。(再此以gap=gap*3+1为公式)
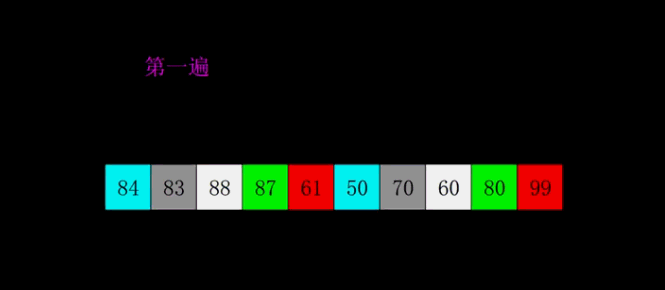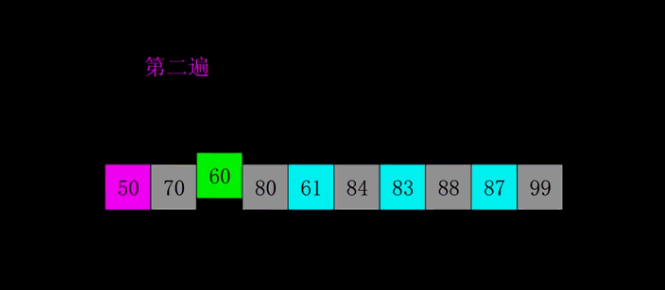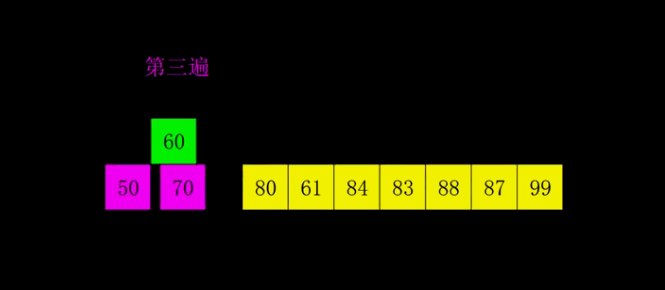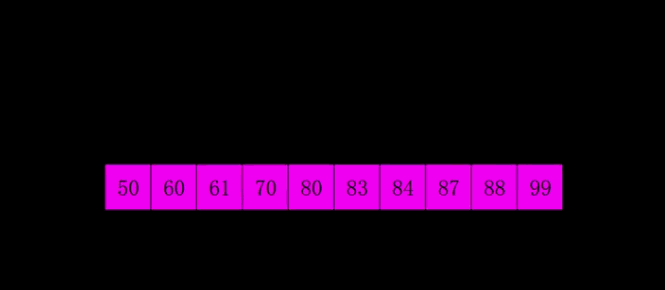
代码实现:
private static void sort(int[] array) {
int n = array.length;
int h = 1;
while (h<n/3) { //动态定义间隔序列
h = 3*h +1;
}
while (h >= 1) {
for (int i = h; i < n; i++) {
for (int j = i; j >= h && (array[j] < array[j - h]); j -= h) {
int temp = array[j];
array[j] = array[j - h];
array[j-h]= temp;
}
}
h /=3;
}
}5.归并排序
- 归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
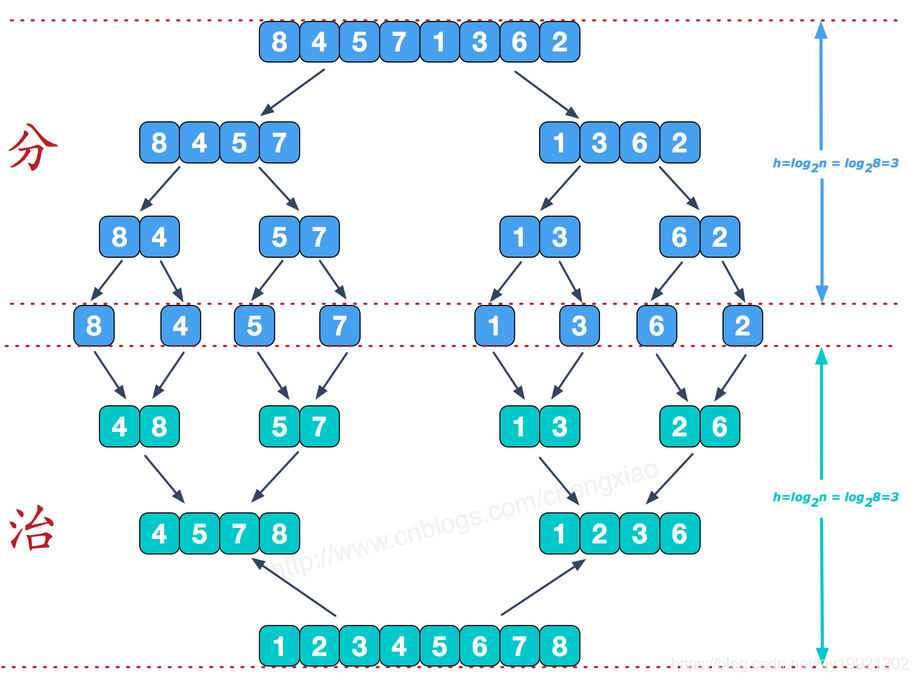
代码实现:
private static void mergeSort(int[] array) {
int[] aux = new int[array.length];
sort(array, aux, 0, array.length - 1);
}
private static void sort(int[] array, int[] aux, int lo, int hi) {
if (hi<=lo) return;
int mid = lo + (hi - lo)/2;
sort(array, aux, lo, mid);
sort(array, aux, mid + 1, hi);
merge(array, aux, lo, mid, hi);
}
private static void merge(int[] array, int[] aux, int lo, int mid, int hi) {
System.arraycopy(array,0,aux,0,array.length);
int i = lo, j = mid + 1;
for (int k = lo; k <= hi; k++) {
if (i>mid) array[k] = aux[j++];
else if (j > hi) array[k] = aux[i++];
else if (aux[j]<aux[i]) array[k] = aux[j++];
else array[k] = aux[i++];
}
}6、快速排序
- 通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
private static void sort(int[] array) {
shuffle(array);
sort(array, 0, array.length - 1);
}
private static void sort(int[] array, int lo, int hi) {
if(hi<=lo+M) {
Insert.sort(a,lo,hi);
return;
}
int lt = lo, gt = hi;
int v = array[lo];
int i = lo;
while (i <= gt) {
if (array[i]<v) exch(array, lt++, i++);
else if (array[i]>v) exch(array, i, gt--);
else i++;
}
// a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi].
sort(array, lo, lt-1);
sort(array, gt+1, hi);
}
private static void exch(int[] a, int i, int j) {
int swap = a[i];
a[i] = a[j];
a[j] = swap;
}
/**
*打乱数组
*/
private static void shuffle(int[] array) {
Random random = new Random(System.currentTimeMillis());
if (array == null) throw new NullPointerException("argument array is null");
int n = array.length;
for (int i = 0; i < n; i++) {
int r = i + random.nextInt(n-i); // between i and n-1
int temp = array[i];
array[i] = array[r];
array[r] = temp;
}
}7、堆排序
堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。

public static void sort(int[] a){
int N = a.length;
int[] keys = new int[N+1];
//注意,堆的数据结构是从1开始的,0不用
for (int i = 1; i < keys.length; i++) {
keys[i] = a[i-1];
}
// //构造堆,使得堆是有序的
for(int k = N/2;k>=1;k--) sink(keys,k,N);
//排序,相当于毁掉堆
while(N>1){
exch(keys,1,N--);
sink(keys,1,N);
}
//重新写回数组
for (int i = 0; i < a.length; i++) {
a[i] = keys[i+1];
}
}
private static void sink(int[] a, int k, int N) {
// TODO Auto-generated method stub
while(2*k<=N){
int j = 2*k;
if (j < N && less(a[j], a[j+1])) j++;
if (less(a[j], a[k])) break;
exch(a, k, j);
k = j;
}
}
private static boolean less(int k, int j) {
// TODO Auto-generated method stub
return k < j;
}
private static void exch(int[] a, int i, int n) {
// TODO Auto-generated method stub
int temp = a[i];
a[i] = a[n];
a[n] = temp;
}8、计数排序
- 将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
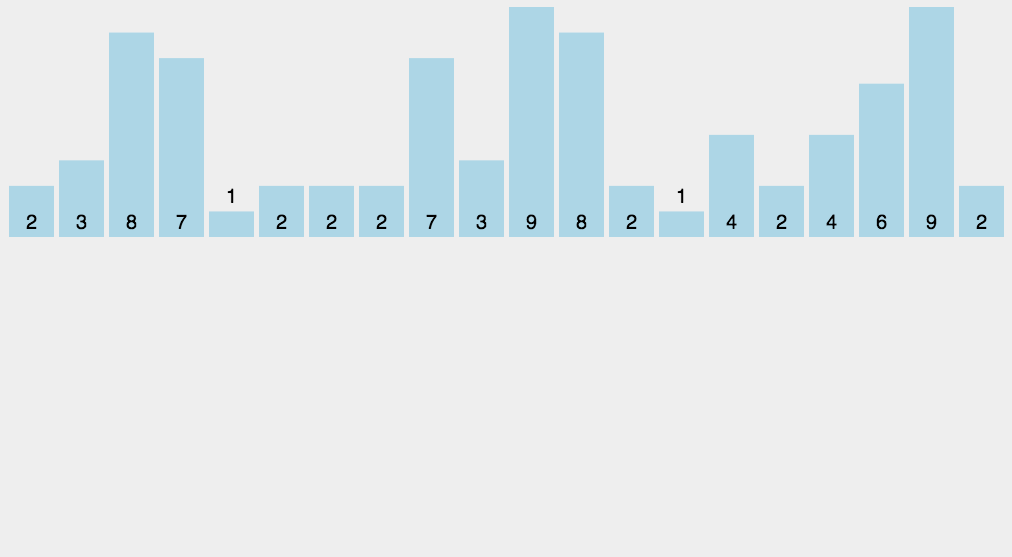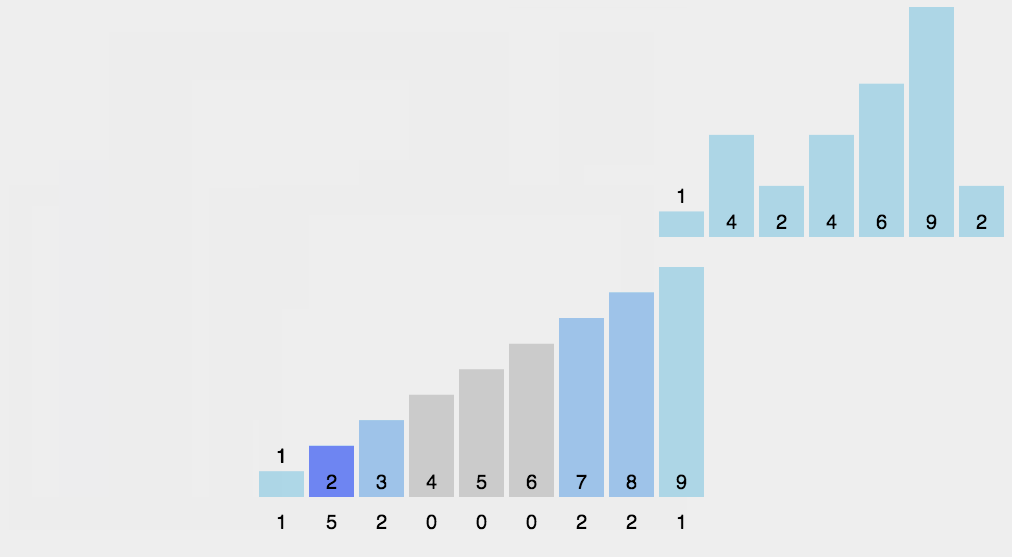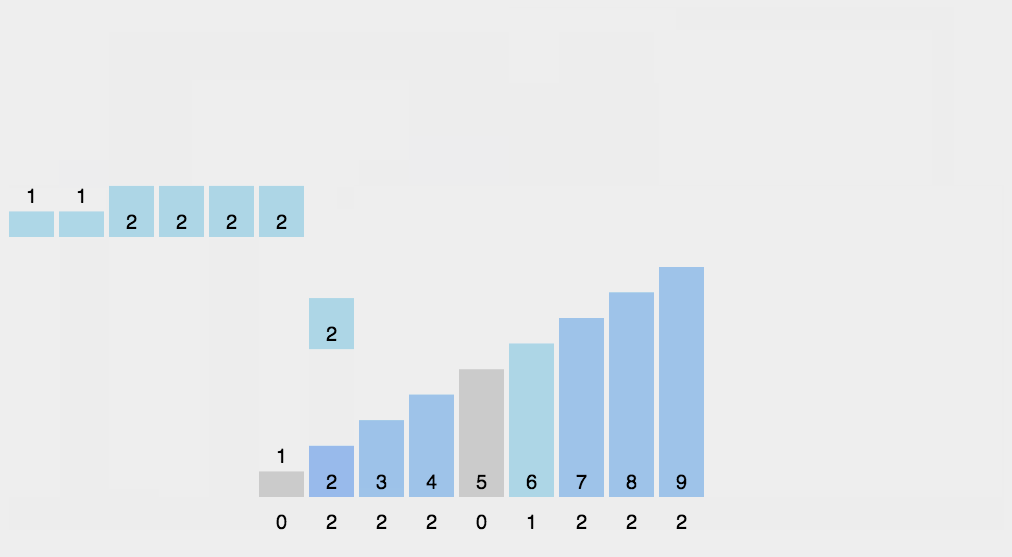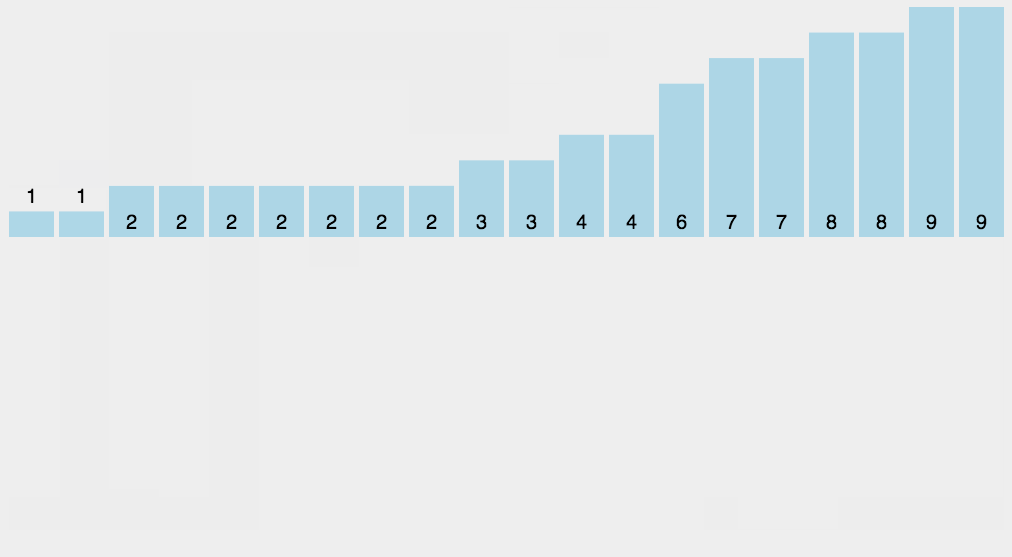
package test;
public class jishu {
public static int[] countingSort(int[] theArray) {
int[] lastArray = new int[theArray.length];
for(int i = 0; i < theArray.length; i++) {
int count = 0;
for(int j = 0; j < theArray.length; j++) {
if(theArray[i] > theArray[j]) {
count++;
}
}
lastArray[count] = theArray[i];
}
return lastArray;
}
public static void main(String[] args) {
int []theArray = {6, 4, 5, 1, 8, 7, 2, 3};
System.out.print("之前的排序:");
for(int i = 0; i < theArray.length; i++) {
System.out.print(theArray[i] + " ");
}
int []resultArray = countingSort(theArray);
System.out.print("计数排序:");
for(int i = 0; i < resultArray.length; i++) {
System.out.print(resultArray[i] + " ");
}
}
}9、桶排序
- 桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
- 设置一个定量的数组当作空桶;
- 遍历输入数据,并且把数据一个一个放到对应的桶里去;
- 对每个不是空的桶进行排序;
- 从不是空的桶里把排好序的数据拼接起来。
package test;
public class tong {
private int[] buckets;
private int[] array;
public tong(int range,int[] array){
this.buckets = new int[range];
this.array = array;
}
/*排序*/
public void sort(){
if(array!=null && array.length>1){
for(int i=0;i<array.length;i++){
buckets[array[i]]++;
}
}
}
/*排序输出*/
public void sortOut(){
//倒序输出数据
for (int i=buckets.length-1; i>=0; i--){
for(int j=0;j<buckets[i];j++){
System.out.print(i+"\t");
}
}
}
public static void main(String[] args) {
testBucketsSort();
}
private static void testBucketsSort(){
int[] array = {5,7,3,5,4,8,6,4,1,2};
tong bs = new tong(10, array);
bs.sort();
bs.sortOut();//输出打印排序
}
}10、基数排序
- 基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
- 取得数组中的最大数,并取得位数;
- arr为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(利用计数排序适用于小范围数的特点);

package test;
/**
* 基数排序
* 平均O(d(n+r)),最好O(d(n+r)),最坏O(d(n+r));空间复杂度O(n+r);稳定;较复杂
* d为位数,r为分配后链表的个数
*
*
*/
public class ji_shu {
//pos=1表示个位,pos=2表示十位
public static int getNumInPos(int num, int pos) {
int tmp = 1;
for (int i = 0; i < pos - 1; i++) {
tmp *= 10;
}
return (num / tmp) % 10;
}
//求得最大位数d
public static int getMaxWeishu(int[] a) {
int max = a[0];
for (int i = 0; i < a.length; i++) {
if (a[i] > max)
max = a[i];
}
int tmp = 1, d = 1;
while (true) {
tmp *= 10;
if (max / tmp != 0) {
d++;
} else
break;
}
return d;
}
public static void radixSort(int[] a, int d) {
int[][] array = new int[10][a.length + 1];
for (int i = 0; i < 10; i++) {
array[i][0] = 0;
// array[i][0]记录第i行数据的个数
}
for (int pos = 1; pos <= d; pos++) {
for (int i = 0; i < a.length; i++) {
// 分配过程
int row = getNumInPos(a[i], pos);
int col = ++array[row][0];
array[row][col] = a[i];
}
for (int row = 0, i = 0; row < 10; row++) {
// 收集过程
for (int col = 1; col <= array[row][0]; col++) {
a[i++] = array[row][col];
}
array[row][0] = 0;
// 复位,下一个pos时还需使用
}
}
}
public static void main(String[] args) {
int[] a = { 49, 38, 65, 197, 76, 213, 27, 50 };
radixSort(a, getMaxWeishu(a));
for (int i : a)
System.out.print(i + " ");
}
}版权声明:本文为tqy19921202原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。