时序模式

2、 根据课堂上所讲的概念，编写程序产生以下时间序列数据（时间可以简化用1,2,3. . . . .表示），每种类型数据至少20条数据。并根据自己想法，使用程序画出相应的图。

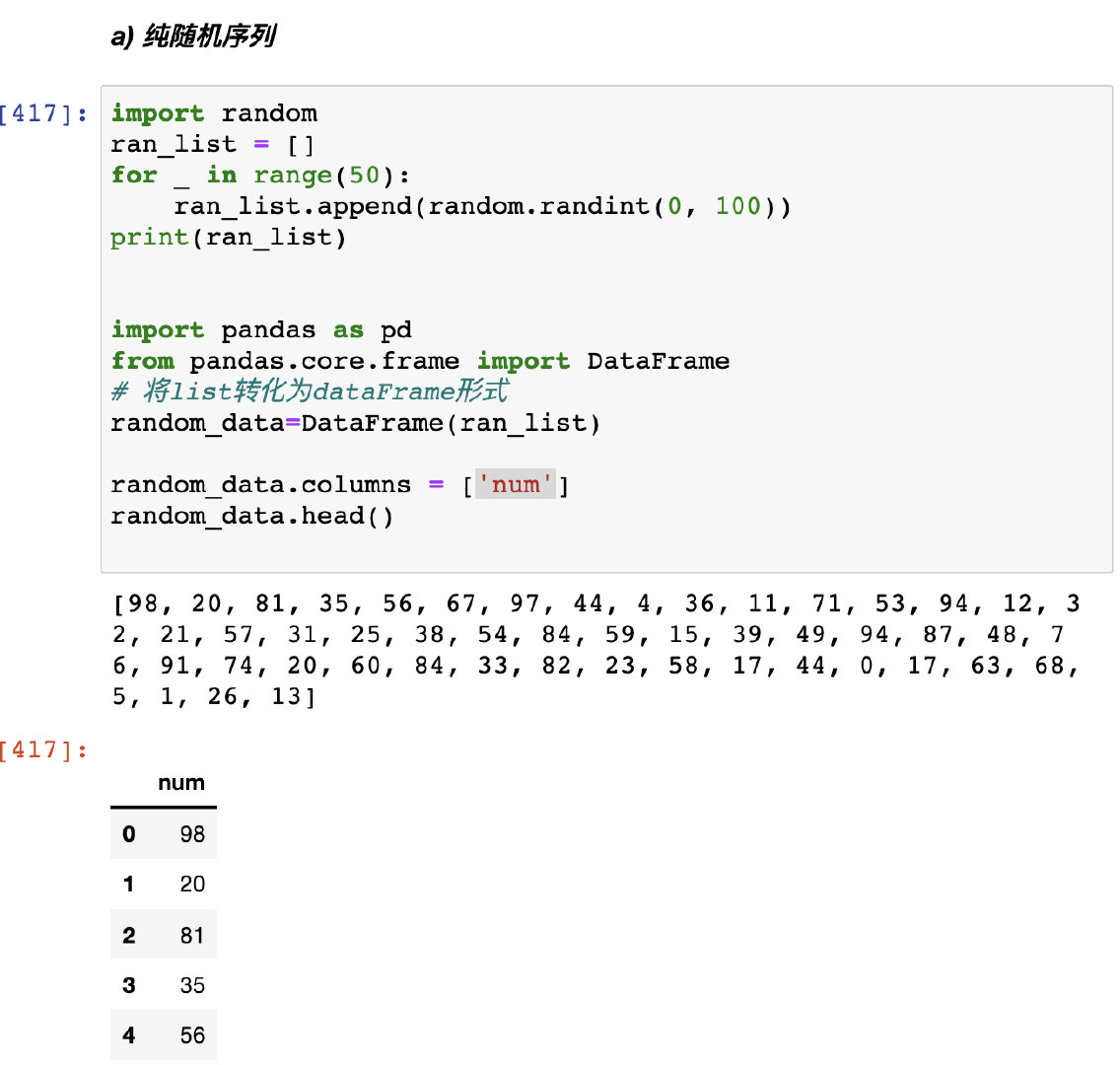
一、 纯随机序列

1、生成随机数据

通过random生成list后将list转化为DataFrame形式

2、白噪音检测查看是否为随机序列

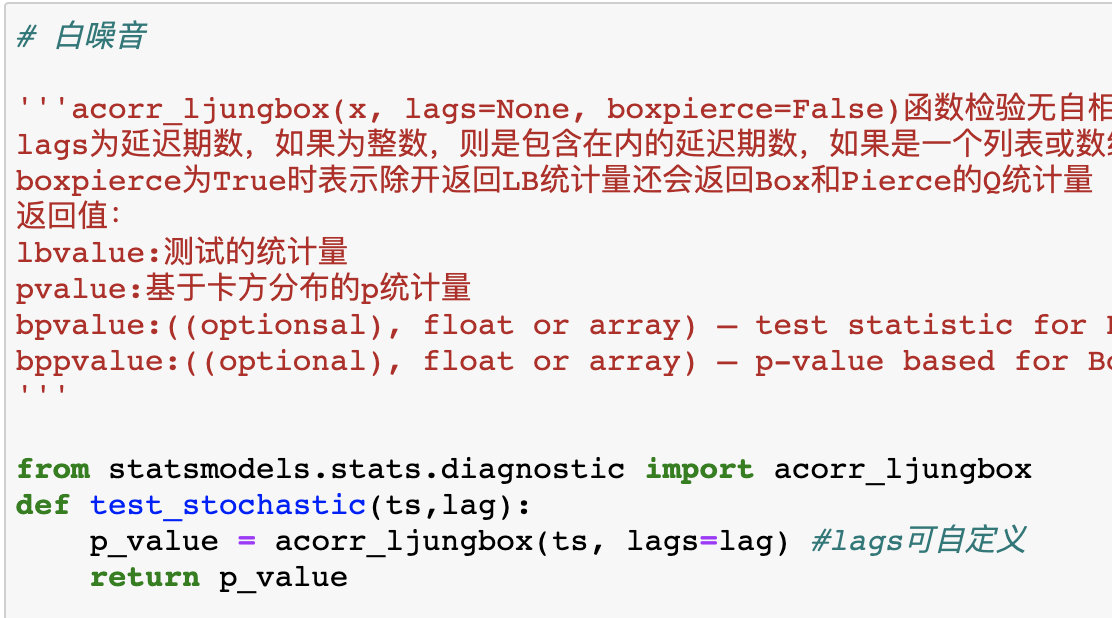
这里可以看到p值为0.47690937，可以认为是一个随机序列

原假设：是随机的，即改序列为白噪声序列。

• p值大，接受原假设；
• p值小，拒绝原假设。

分割线：0.05。 0.05置信区间以下，可以认为出现显著的自回归关系，且序列为非白噪声。

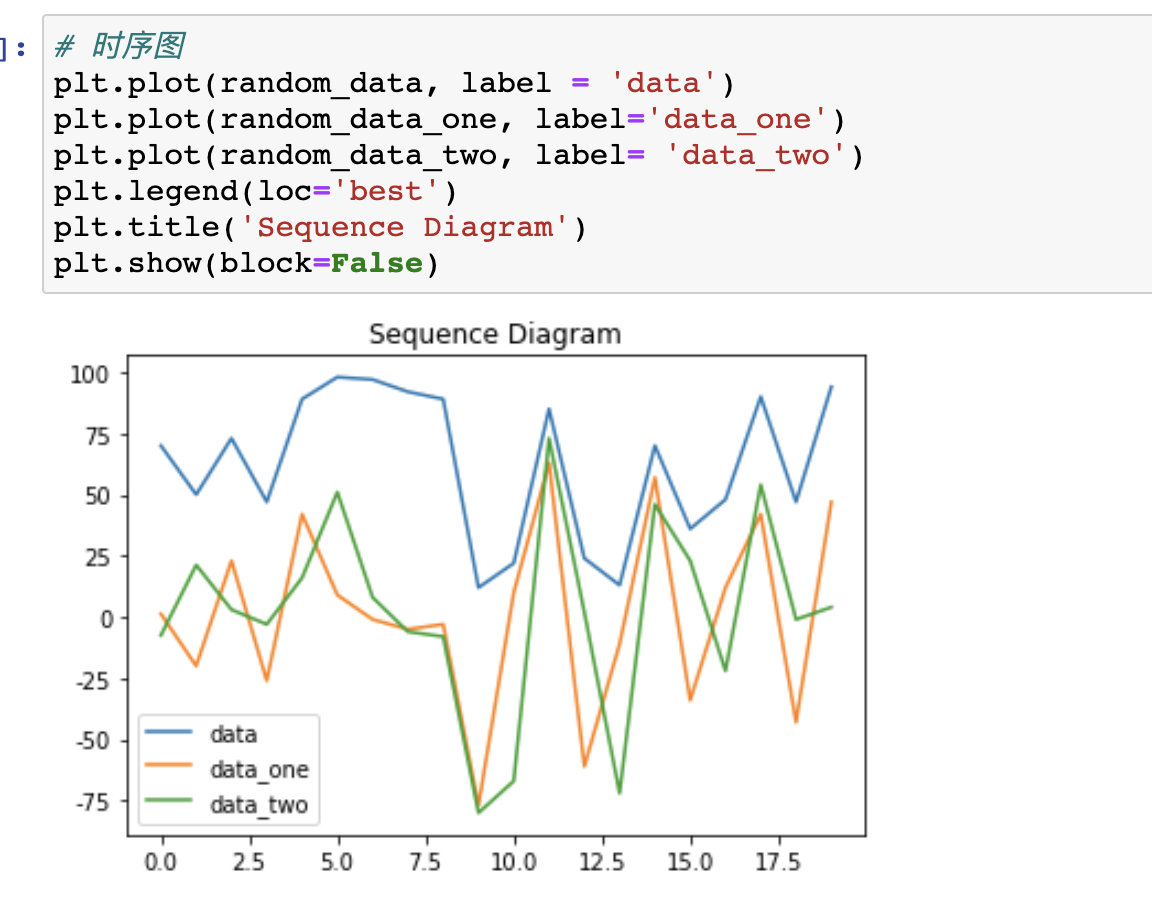
3、查看时序图

生成的数据为random_data

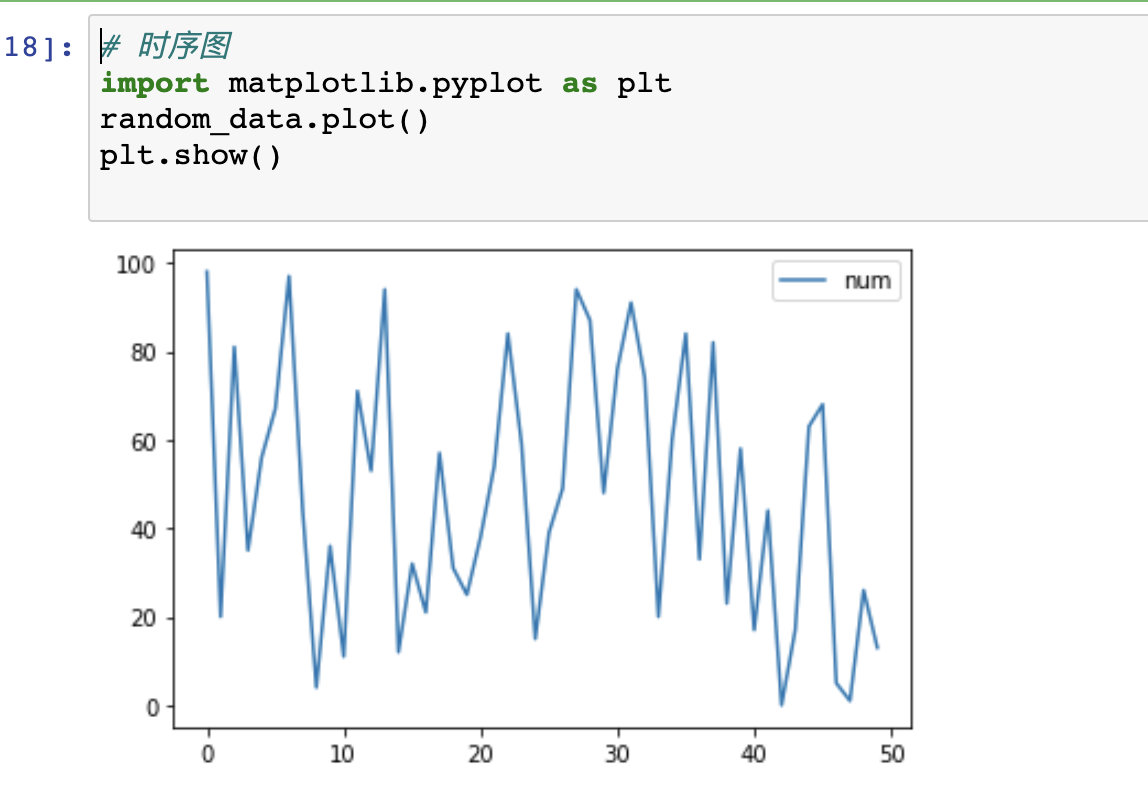
可观察到时序图的数据波动较大

4、ADF检验

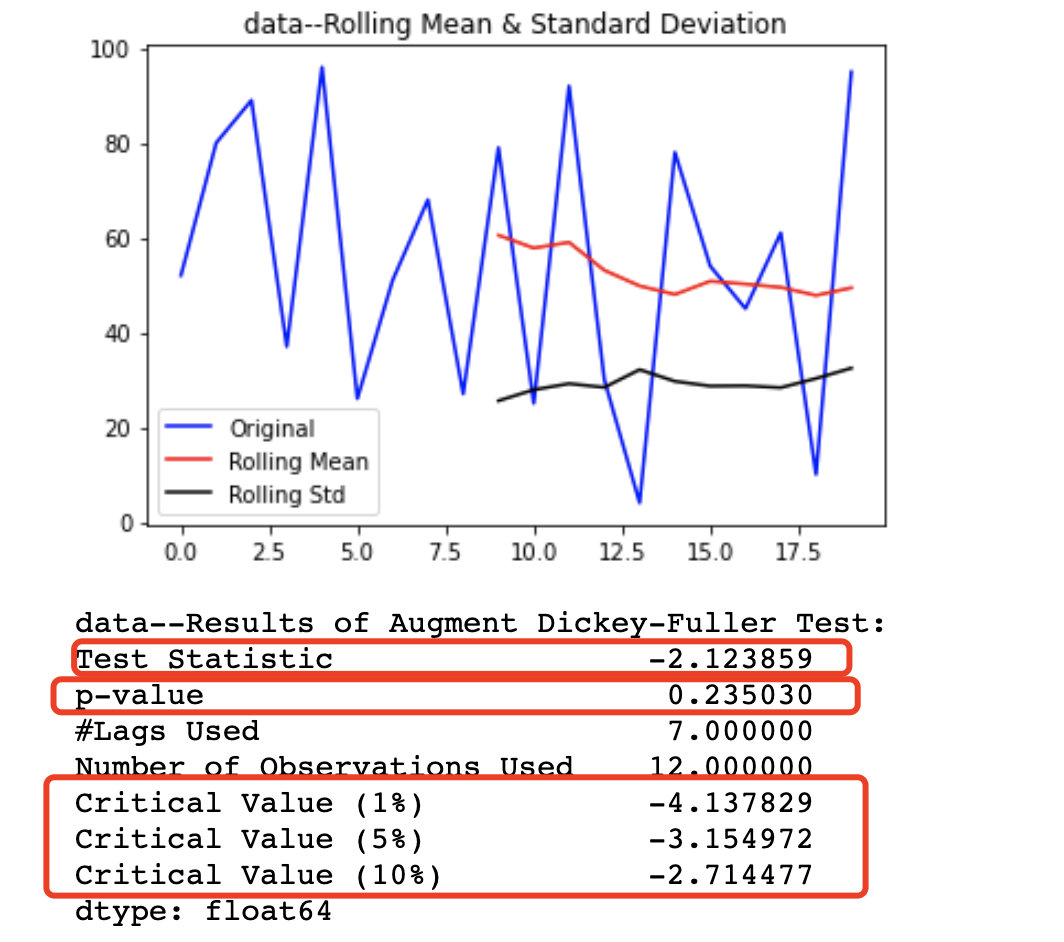
• 假设序列为不平稳序列
• 看p值和显著性水平：
  • p-value为0.235030大于0.05，可以认为序列是不平稳的
• 看检验统计量Test statistic和临界值Critical Value：
  • ts值-2.123859均大于cv值，可以接受原假设，认为序列是不平稳的；

这里想看看当把生成的数据扩大为200个后是否随机序列仍然是平稳的，随后我将数据扩大生成200个后，真的平稳了…

200个数据后：

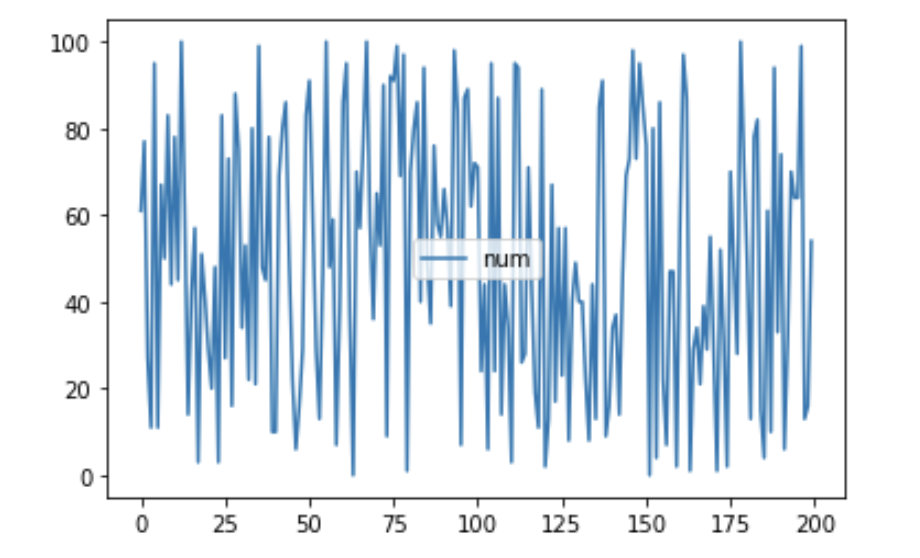
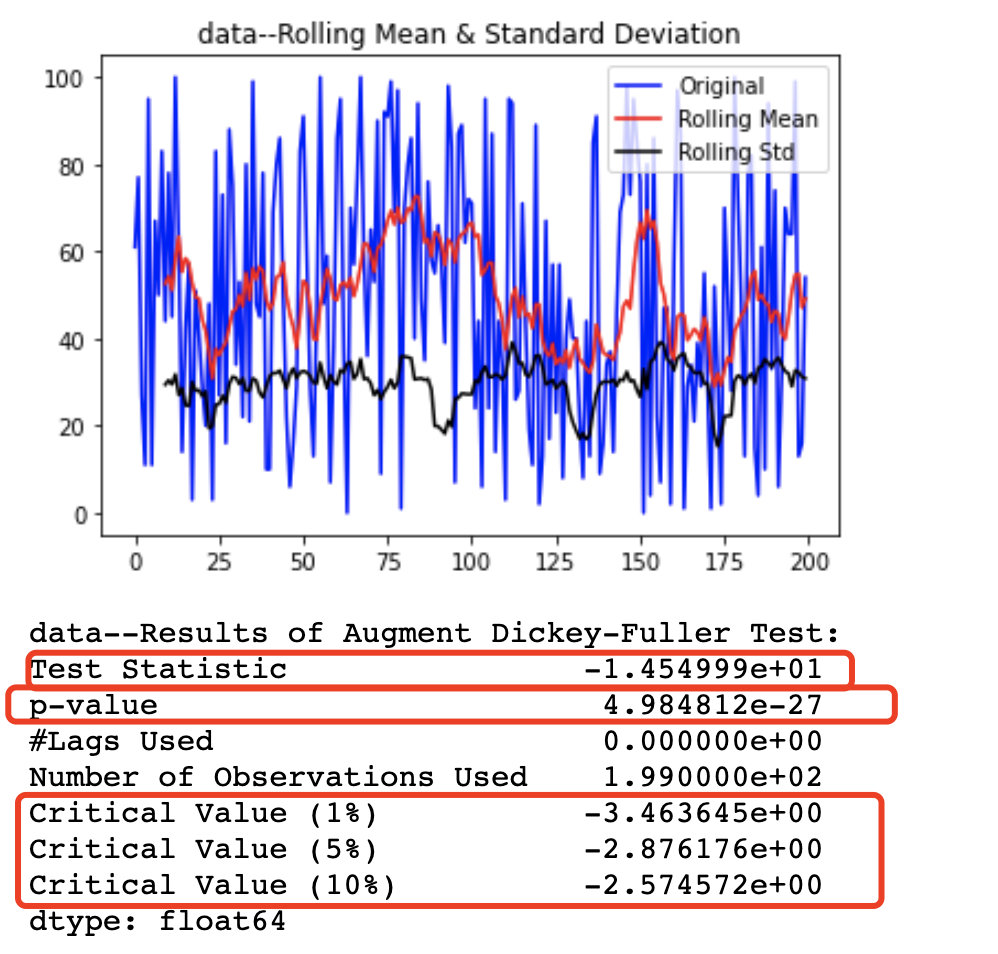
再次分析：

• p值与å（阿尔法值）
  • 4.9e-27远远小于0.05 可以拒绝假设，即认为序列是平稳的
• ts和cv值
  • ts值约为-14.5，而cv值均为0.2、0.3左右，可以认为序列为平稳序列

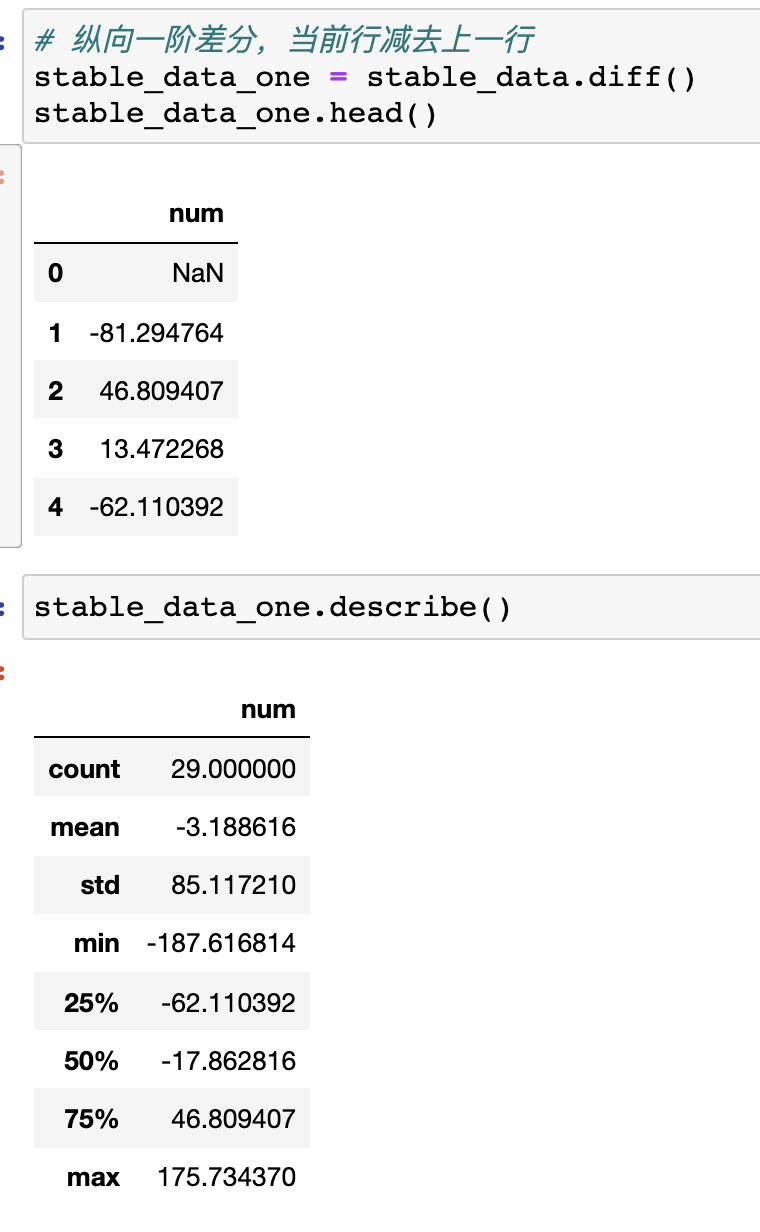
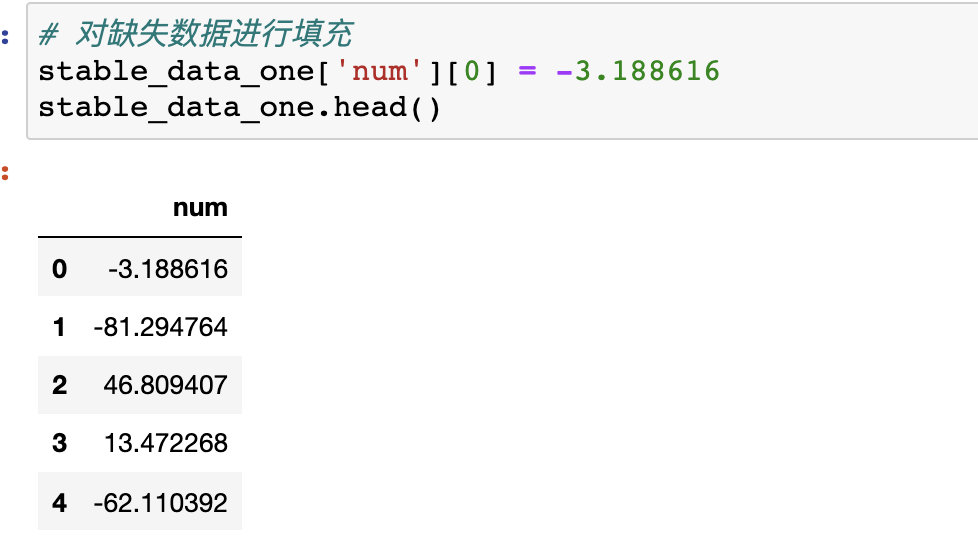
之后我将序列进行了一阶差分

4、一阶差分

进行ADF

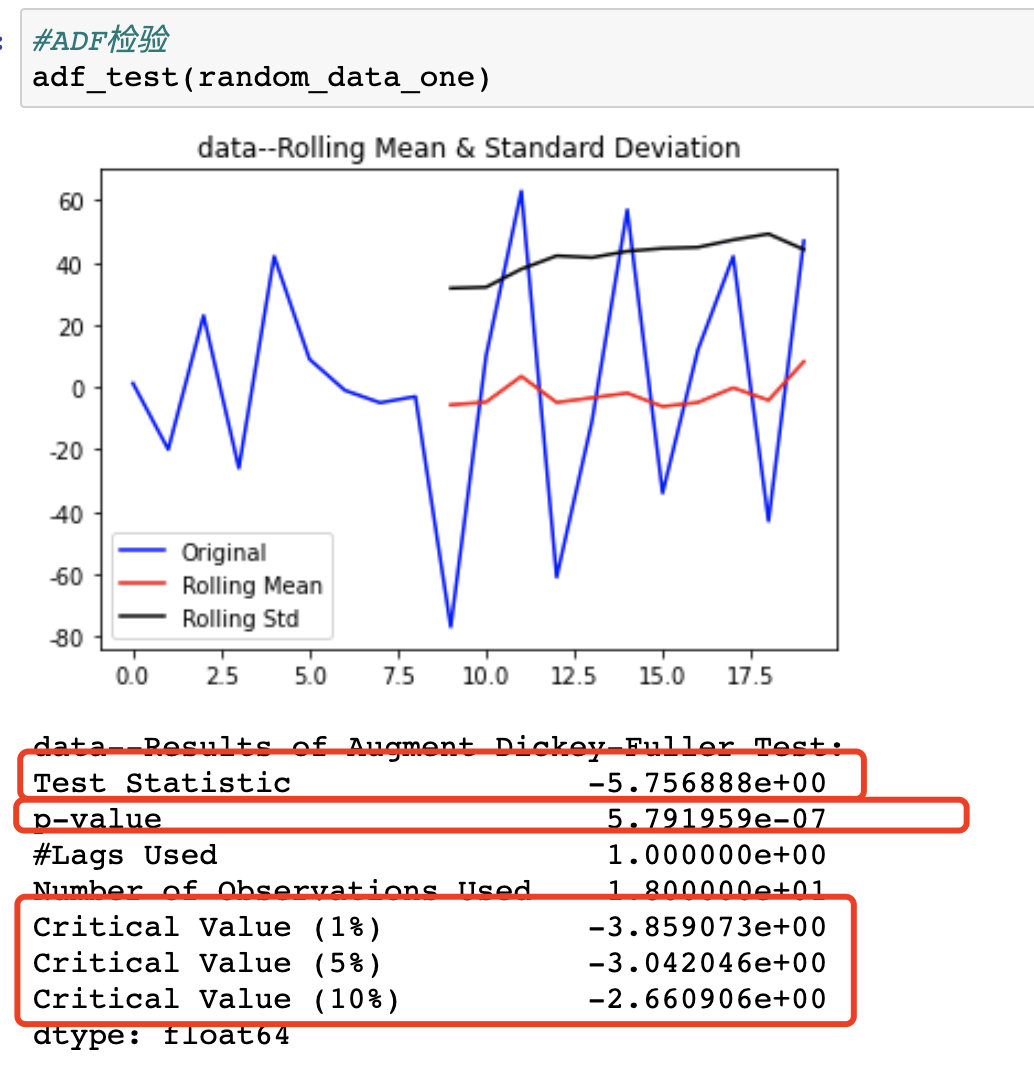
可以发现p值明显小于了0.05，同时ts值也均小于cv值

可以认为该序列为一个平稳序列

5、查看自相关图和偏自相关图

查看元序列和一阶拆分后数据的自相关图和偏自相关图

• 原序列：

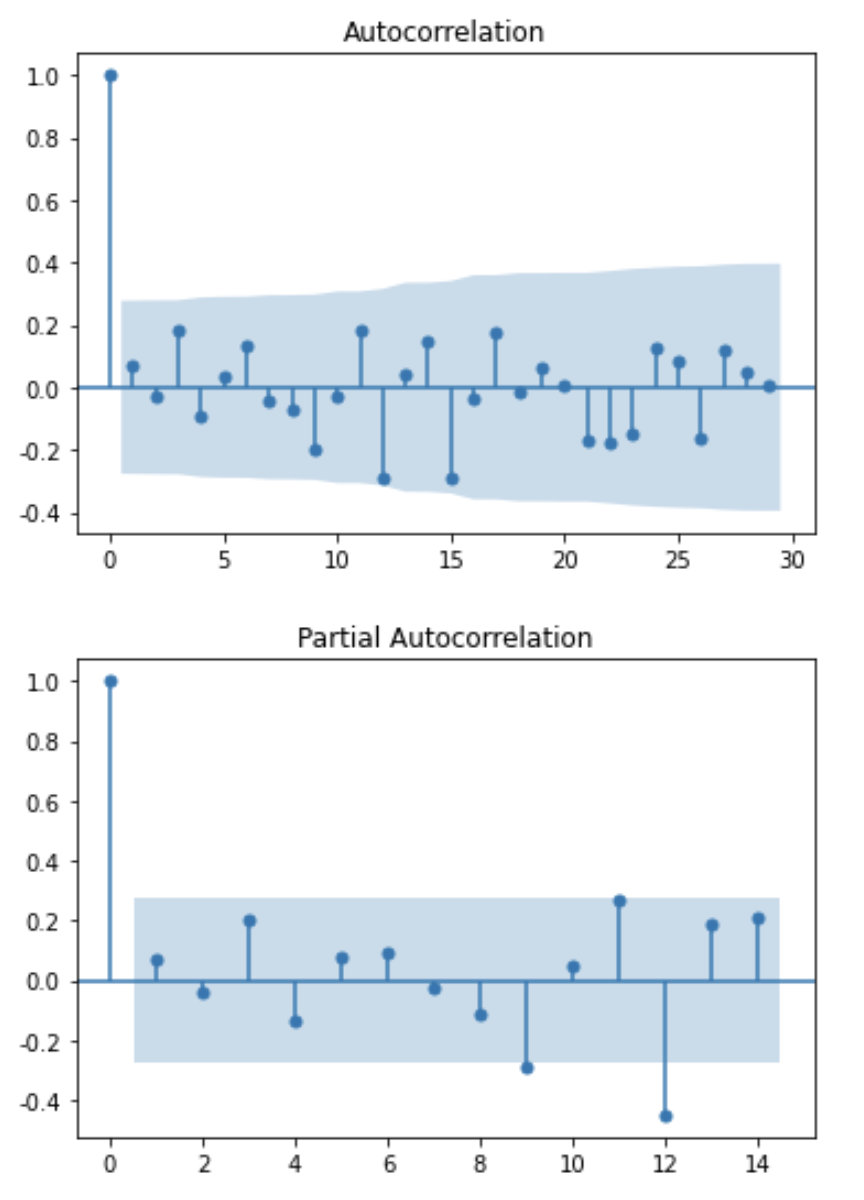
可以发现自相关图在1阶数据一直在2倍标准差范围内波动，可以认为该序列为自相关系数的1阶拖尾。

而偏自相关图的数据也呈现1阶拖尾。

因此如果需要选择模型可以选择ARMA。

• 一阶差分后

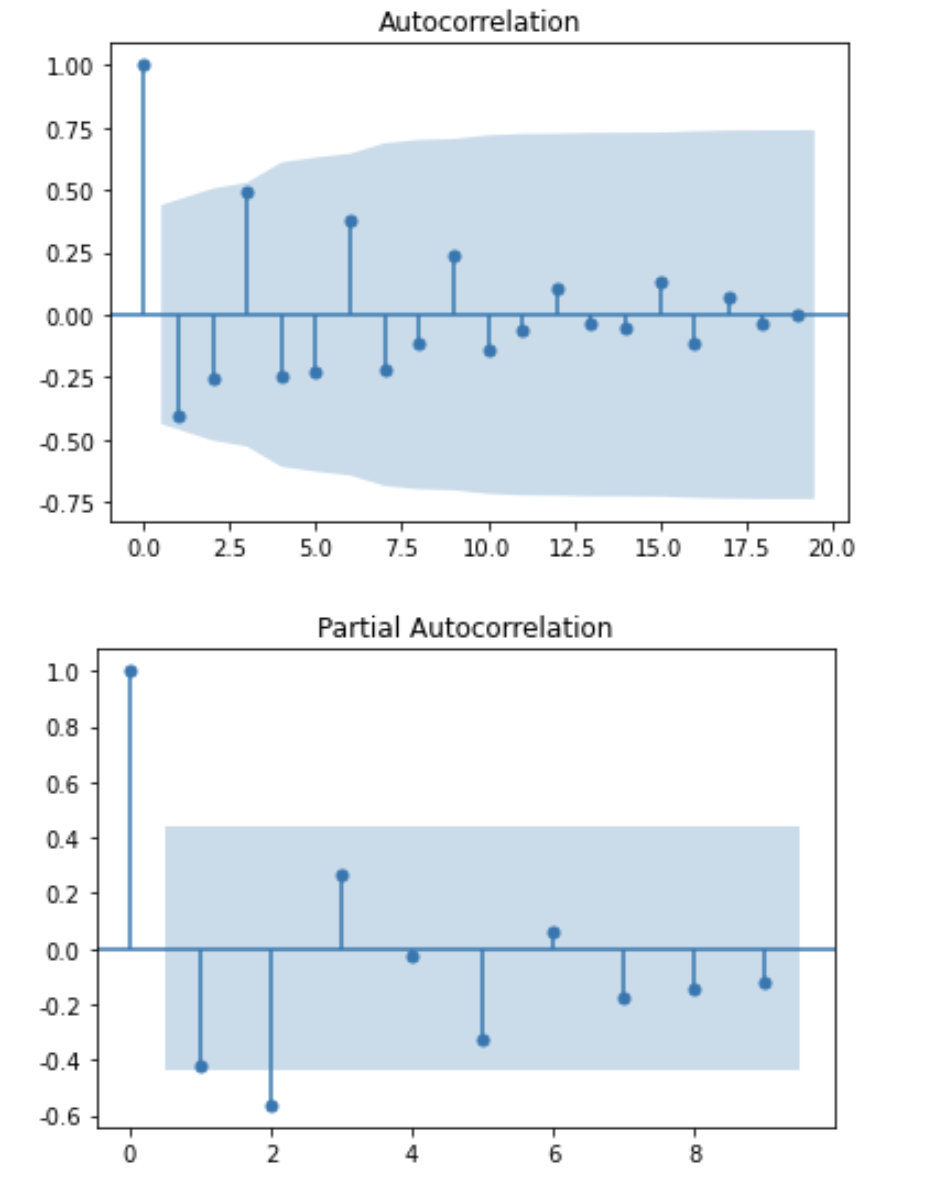
自相关系数与偏自相关系数，拖尾与截尾：https://blog.csdn.net/lyp_1020k/article/details/109420638

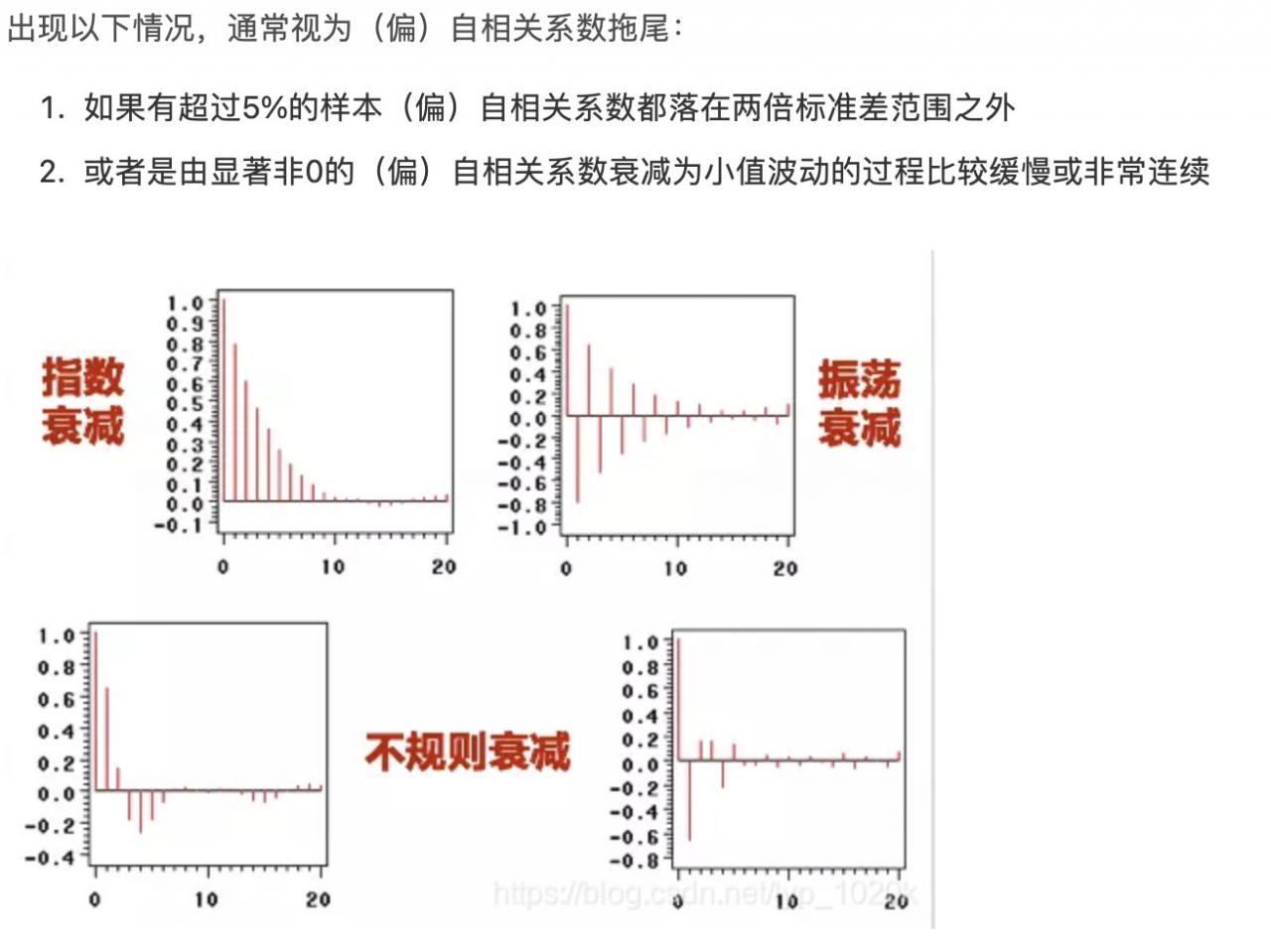
根据自相关图和偏自相关图的拖尾或截尾可以开始选择建模模型

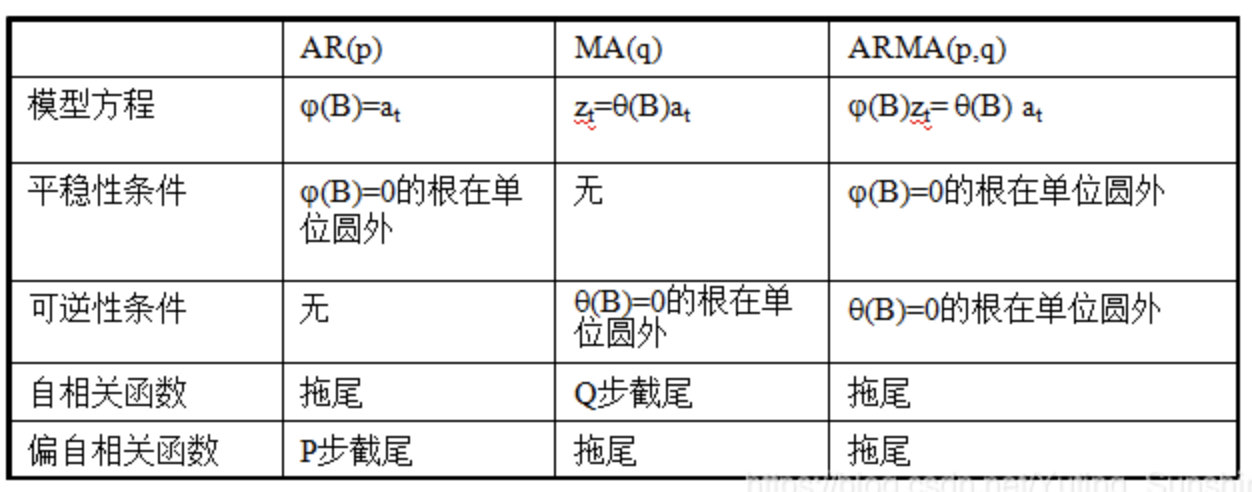
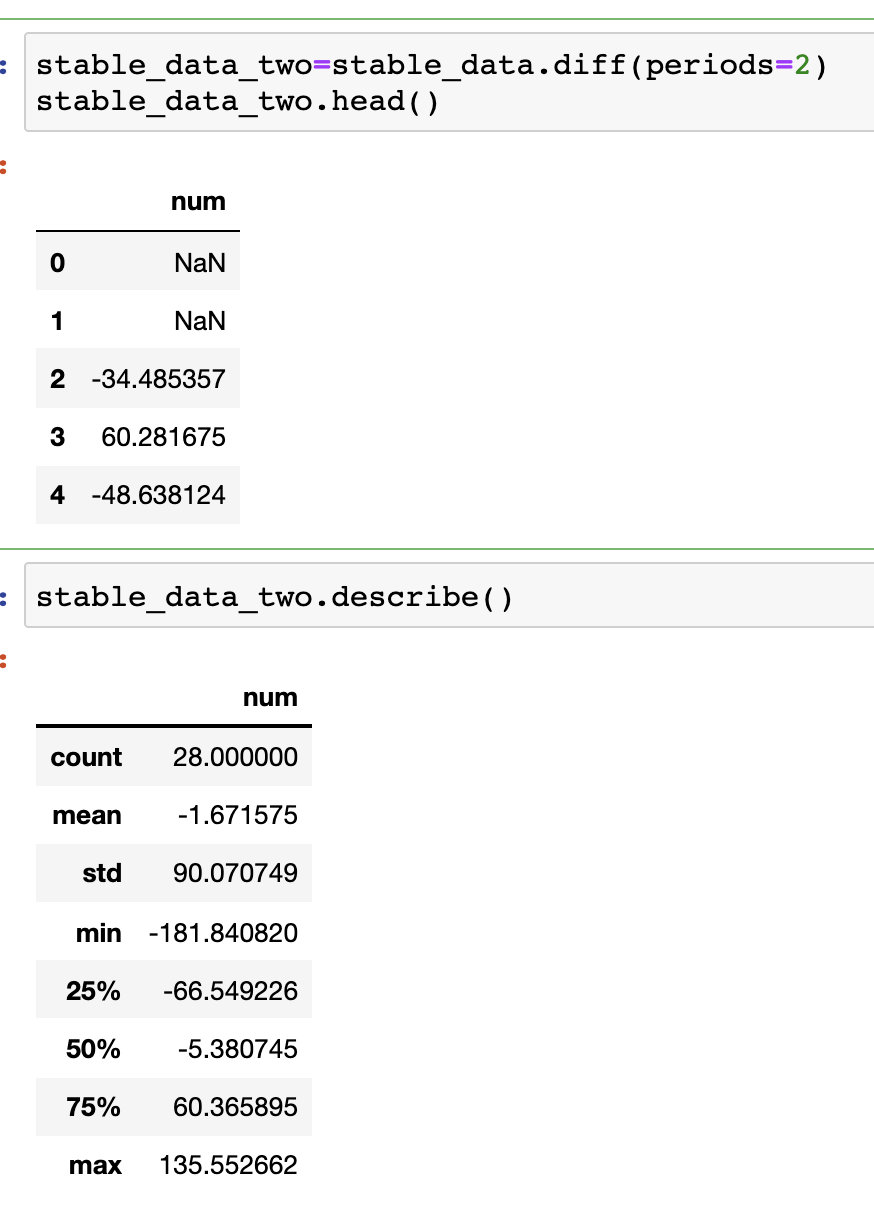
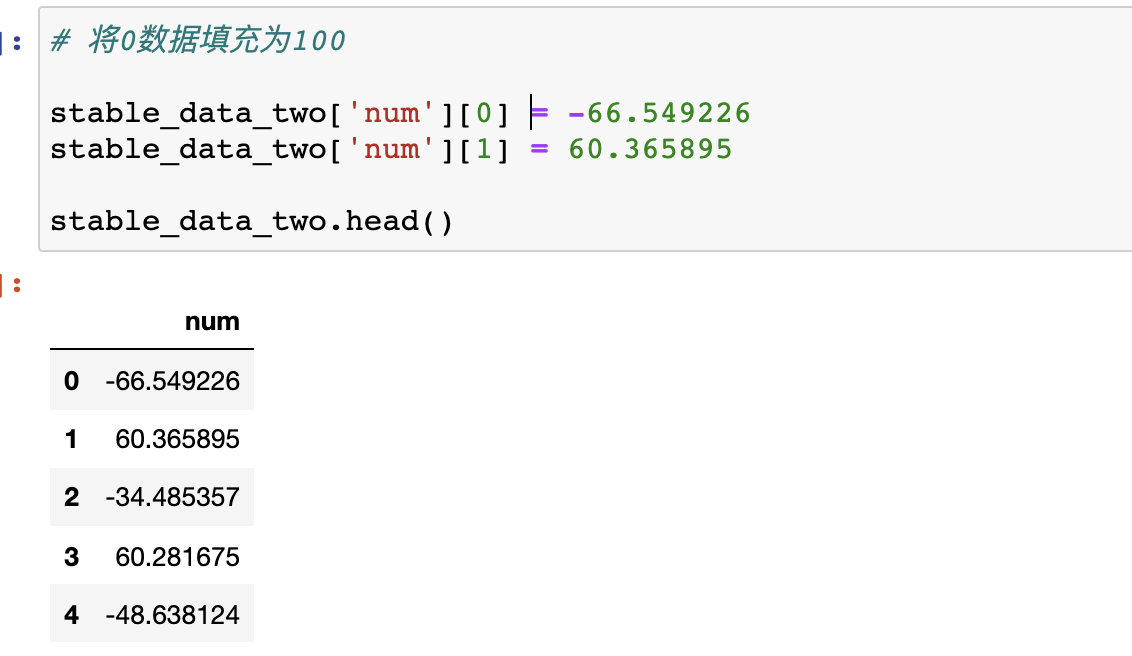
6、将随机序列一阶拆分和二阶拆分后

二、 平稳序列

1、生成数据

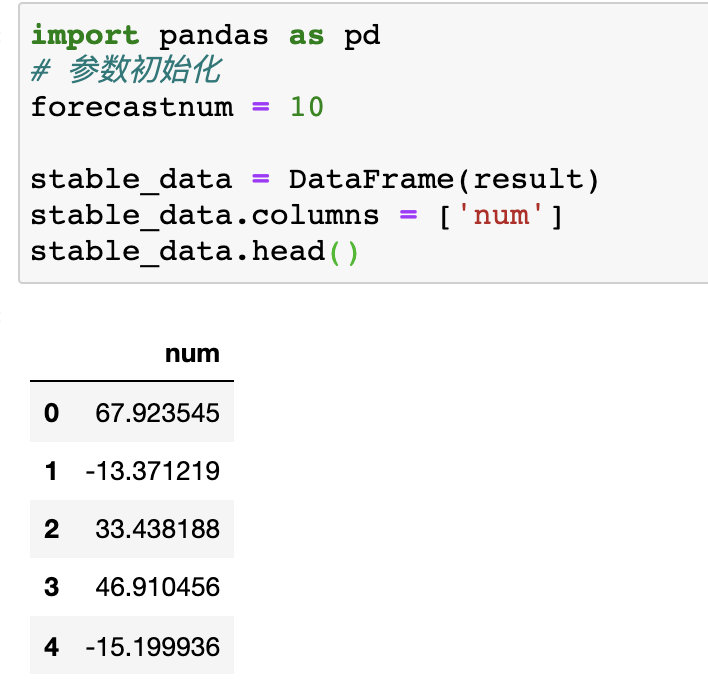
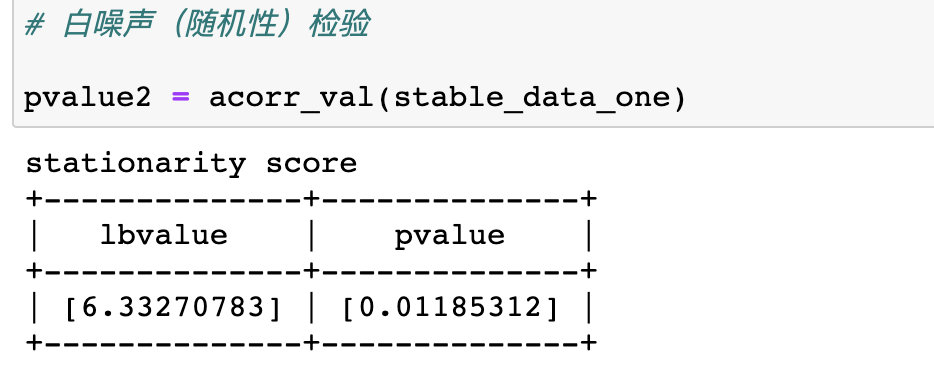
2、白噪音

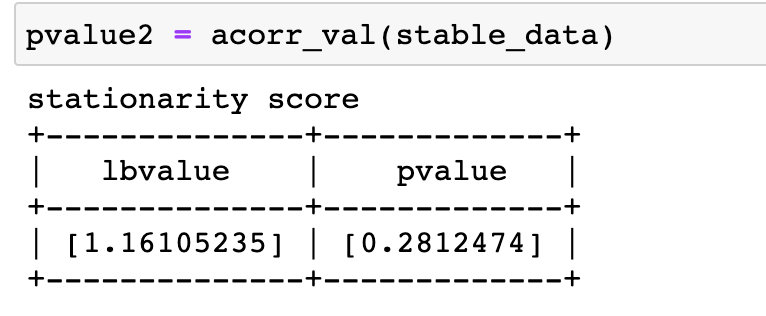
这里可以看到p值为0.2812474，大于0.05，可以认为是一个随机序列，

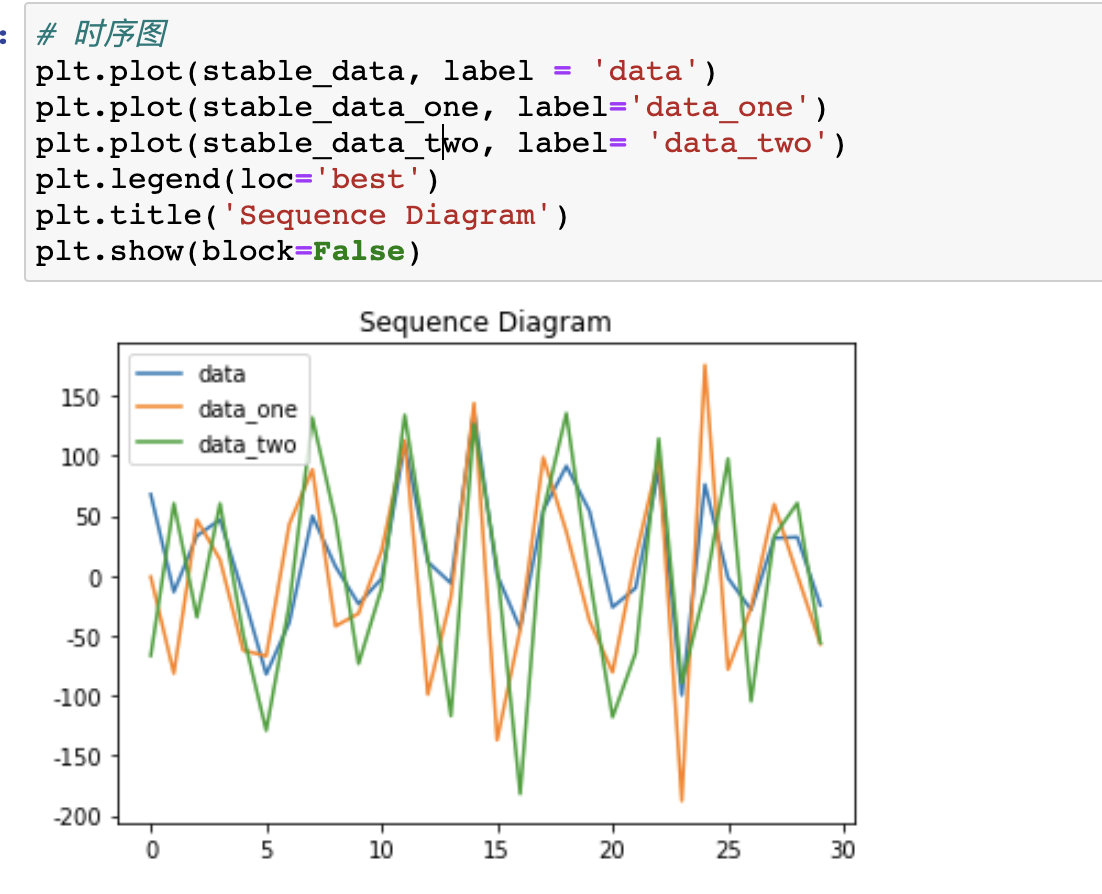
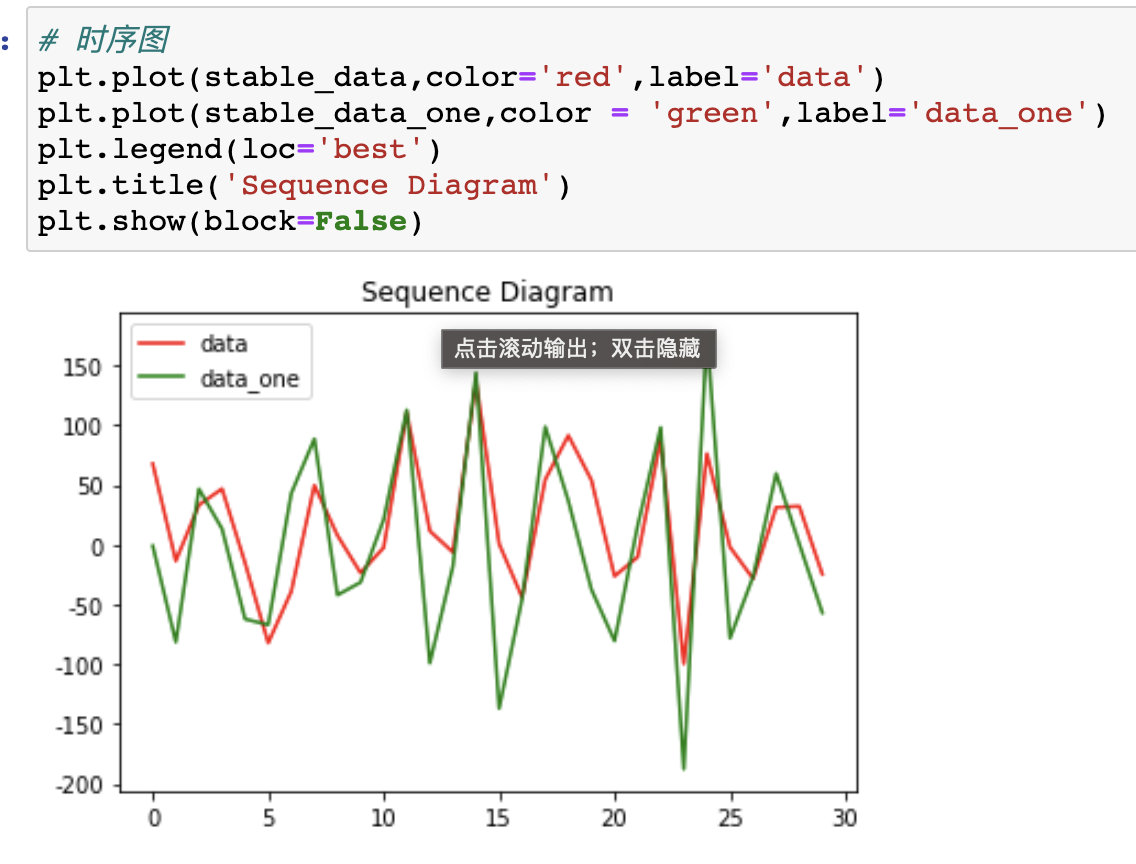
3、时序图

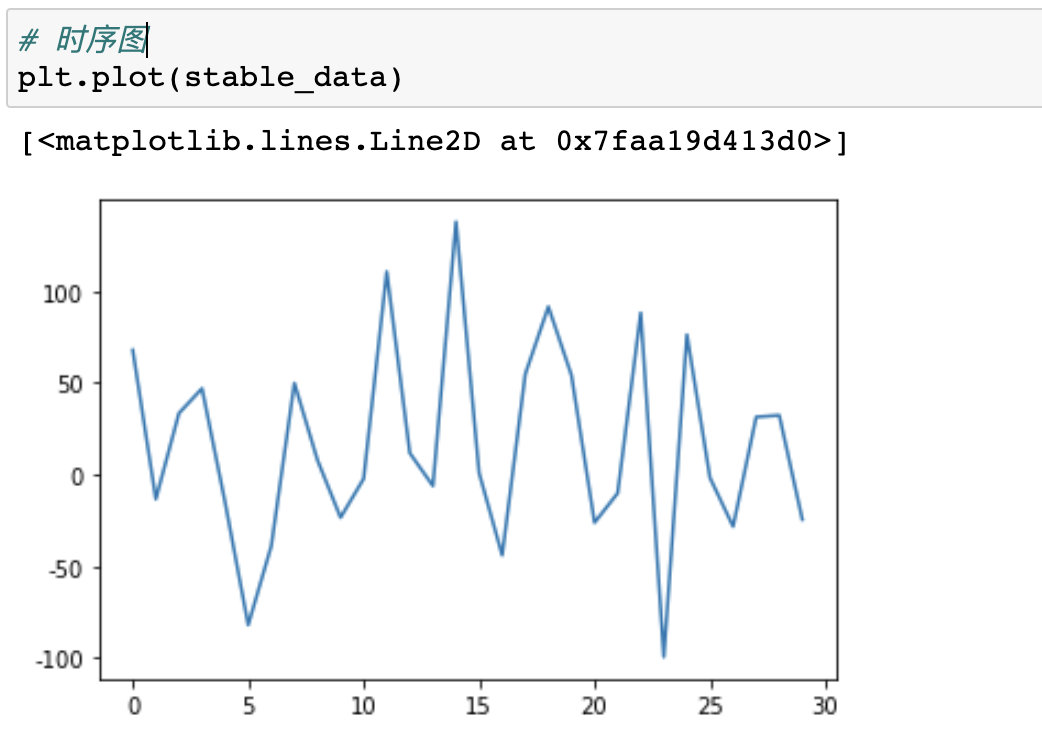
4、ADF检验

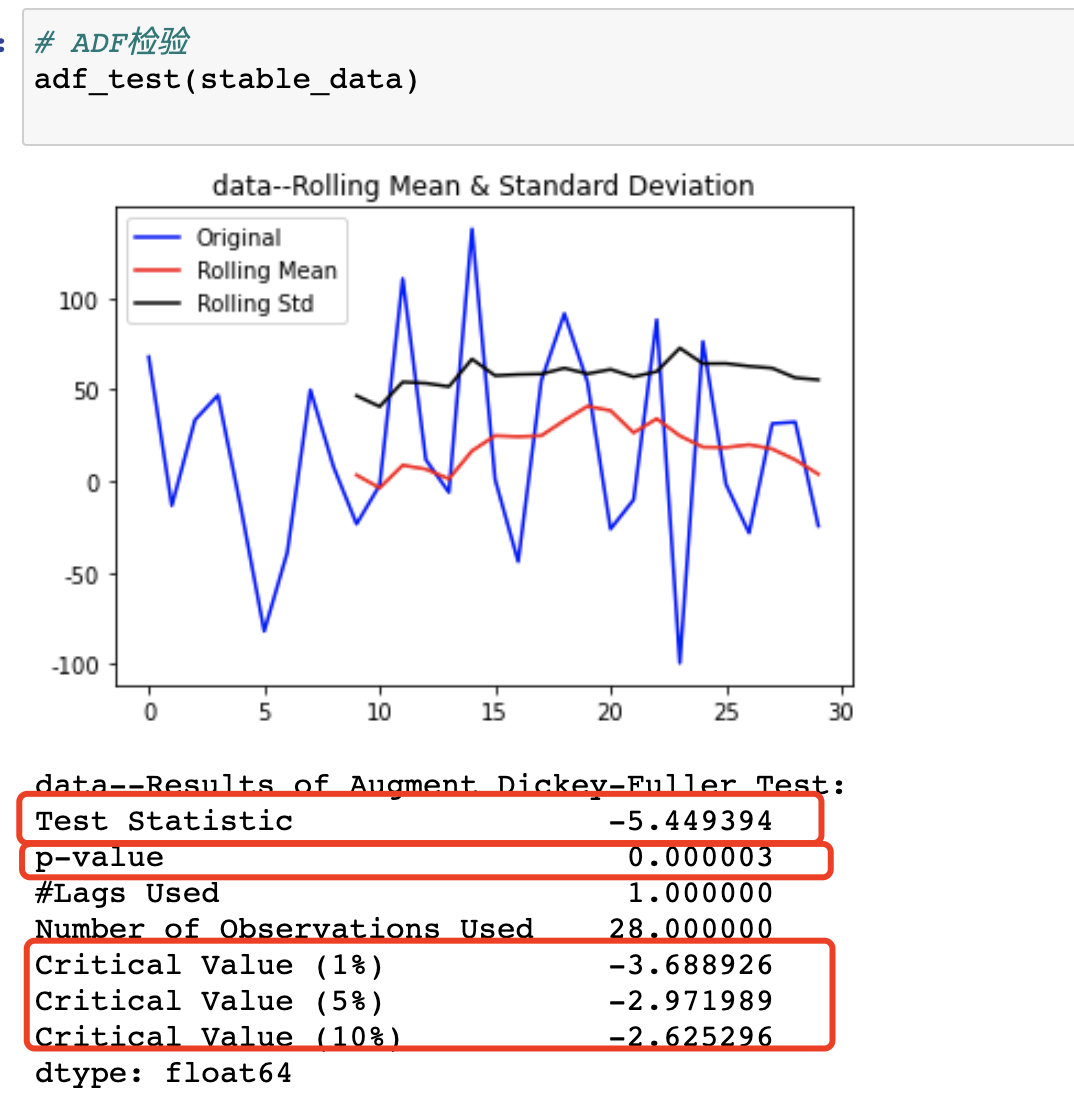
• p值：0.000003小于0.05 平稳
• ts 值 << cv值。平稳

1、 假设不平稳

2、 p和显著性水平 ：
p值1.99e-07远远小于0.05，
可以拒绝原假设，即认为序列是平稳的

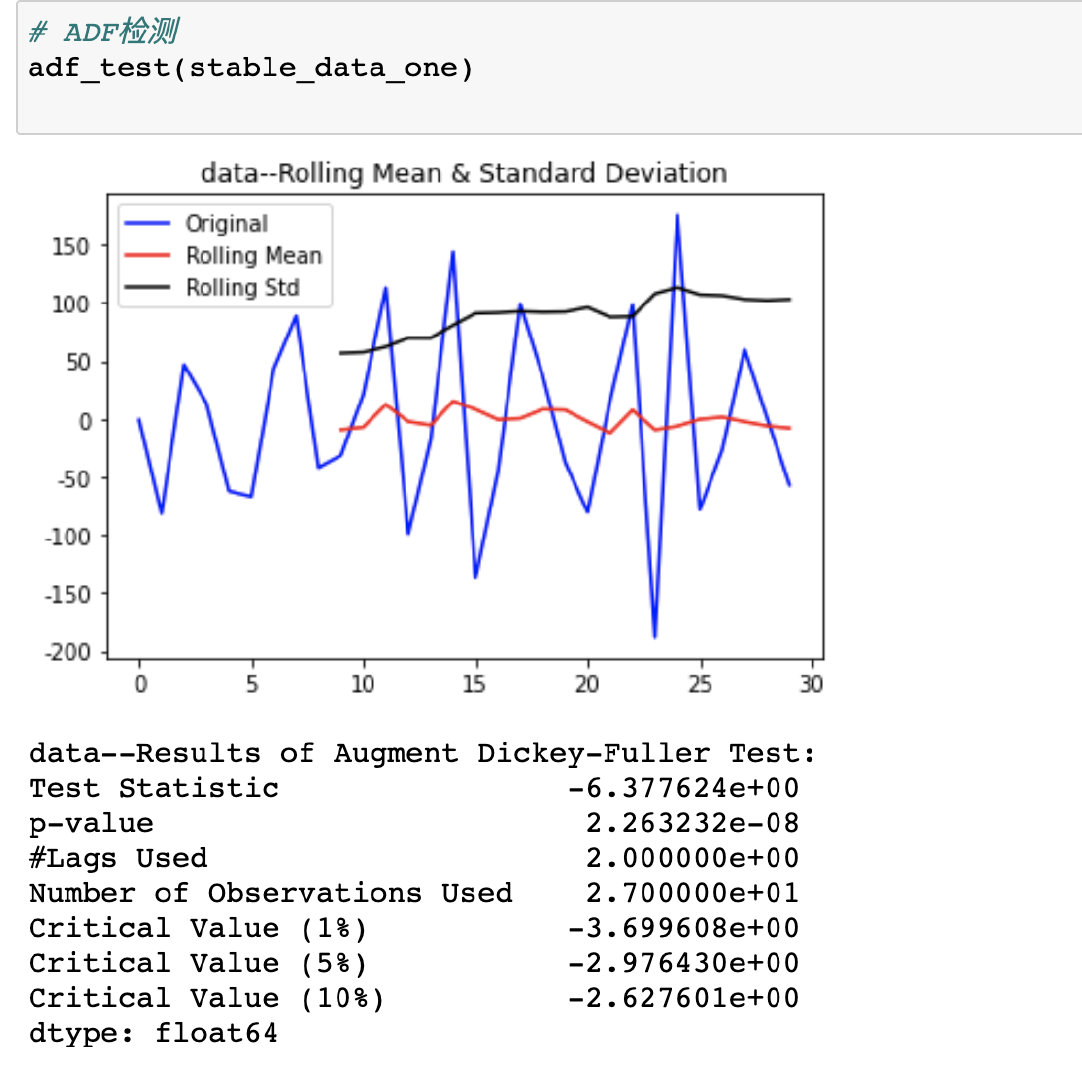
3、 检验统计量Test statistic和临界值Critical Value：
ts为-5.96 均小于 cv值 -3.6，
可以拒绝原假设，认为序列是平稳的；

5、acf && pacf

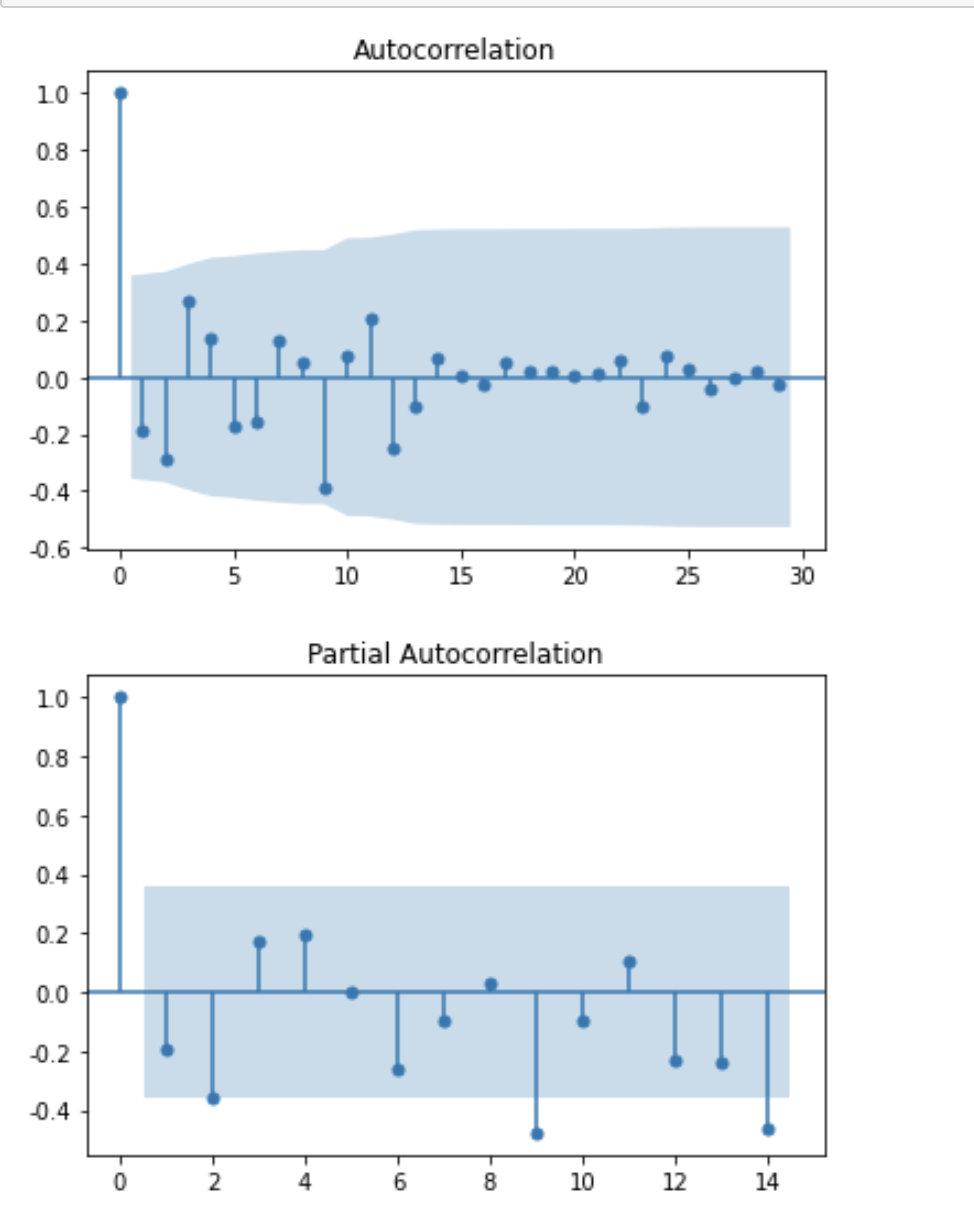
这里很显然是一个拖尾
除了1阶的自相关系数在2倍标准差范围之外
其他的均在2倍范围内波动

在2倍标准差范围内波动
一阶拖尾

截尾：在大于某个常数k后快速趋于0为k阶截尾
拖尾：始终有非零取值，不会在k大于某个常数后就恒等于零(或在0附近随机波动)

三、 1阶平稳序列

四、 2阶平稳序列