参考《数据结构-java语言描述》
队列是一种运算受限的线性表,只能在一端进行数据元素的添加,在另一端进行删除。允许添加的一端被称之为队尾(rear),允许删除的一端被称为队头(front)
添加操作称之为入队,删除操作称之为出队
队列遵循先进先出(FirstInFirstout)的原则
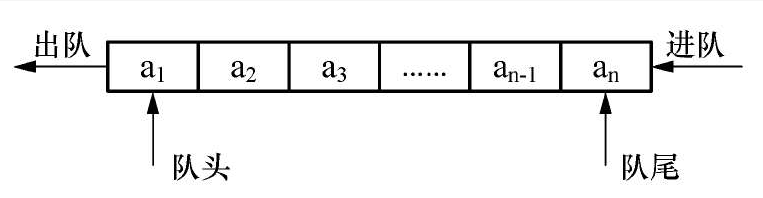
上图为队列示意图
队列的基本操作
1、初始化 -- 构造一个空队列
2、入队 -- 在队列的尾部插入一个新的数据元素
3、出队 -- 删除队列头部的元素
4、获取对头 -- 获取对头数据元素
5、求长度 -- 获取队列中数据元素的个数
6、判空 -- 判断当前队列是否为空
7、正序遍历 -- 依次访问队列中的每一个元素
8、销毁 -- 销毁一个已存在的队列
下述代码为队列的泛型接口定义:
public interface SequenceQueue<T> {
//入队
public void enQueue(T obj);
//出队
public T delQueue();
//获取队头数据元素
public T getHead();
//求队列长度
public int size();
//判空
public boolean isEmpty();
//正序遍历
public void nextOrder();
//销毁
public void clear();
}顺序队列
在顺序队列中,除了一组地址连续的存储单元存储队列中的各个数据元素,还需要一个指向队头的指针(front)和一个指向队尾的指针(rear)。
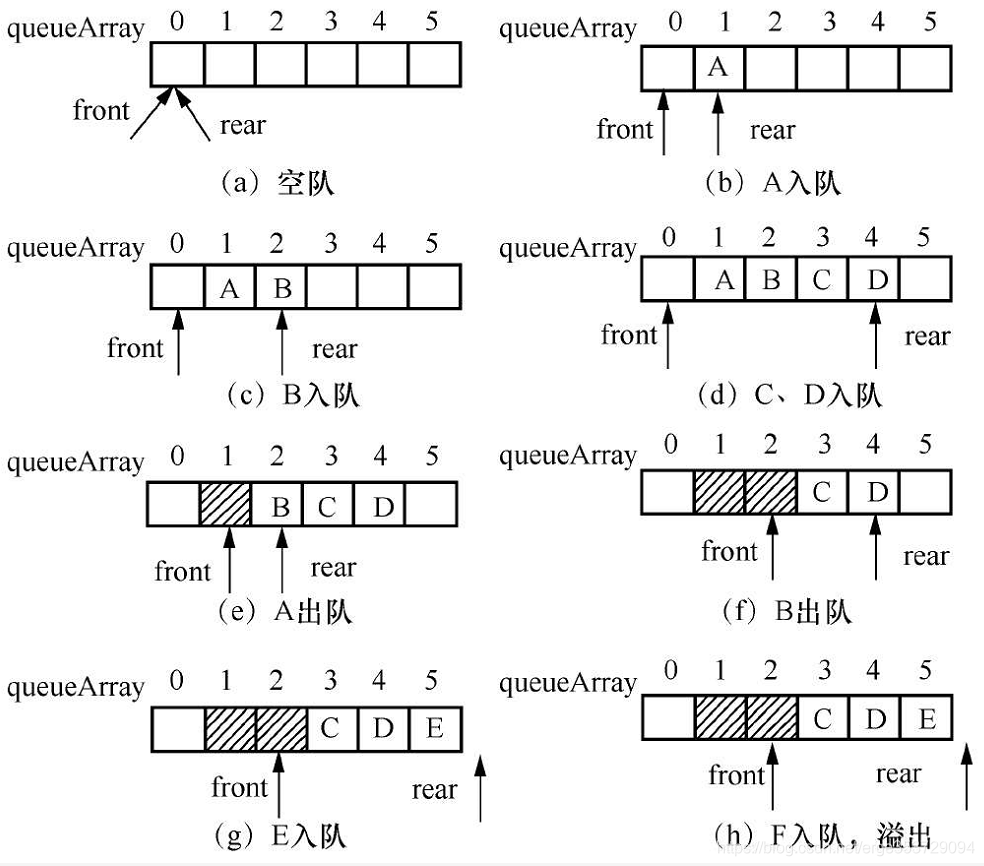
顺序队列入队和出队示意图
队列中的元素数目等于0称为空队列,初始化空队列时,设front=rear=0。入队时,将队尾指针rear加1,同时,把新增的数据元素插入real指针指向的位置;出队时,front=front+1,在将front指针所指的数据元素取出。
由于入队和出队操作都是在队列的两端进行,随着数据元素的不断插入、删除。两端都会向后移动,队列会很快的移动到数组末端造成溢出,而前面的存储单元无法利用。队列中有剩余空间,但无法插入新的元素,这种情况称之为假溢出。
解决上述假溢出的解决方案有两种,
一)、对头固定在数组的第一个单元,每删除一个数据元素后,整个队列向前移动一位
缺点:增加额外开销,时间复杂度为O(n) (不推荐)
二)、循环队列,使用循环队列,除非整个数组空间真正的被全部占用,否则不会出现溢出现象。
循环队列牛逼的地方就是把时间复制度为O(n)(线性阶)的算法变为了O(1)(常量阶)算法
循环队列示意图如下:
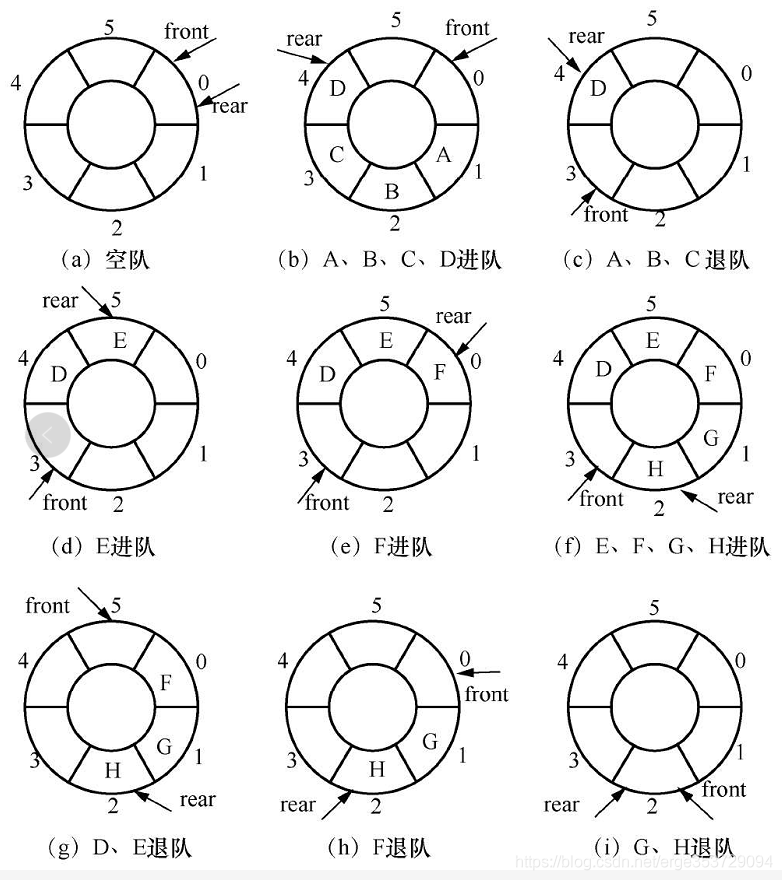
循环队列就是将顺序队列的存储区假象为一个头尾相连的圆环。循环队列中同样有一个指向一个对头的指针front,一个指向队尾的指针指向rear。初始化时,都会被设置为0。
当循环队列进行入队操作时,队尾的指针的表达式从之前的加1,修改为:
rear=(rear+1)%queueArray.lenght (queueArray.length为数组的初始长度)
当循环队列进行出队操作时,对头的表达式为:
front=(front+1)%queueArray.lenght
队列的长度的表达式为:
(rear-front+queueArray.lenght)%queueArray.length
在循环队列中纯粹的使用front==rear,无法判断是队空还是队满。这种情况一般有两解决方案
一)、设置一个flag的标志位,初始值为0,当进行入队操作时,flag加1,出队操作时,fag减1。这样,通过判断flag是否为一个大于0的数,在结合front==rear,可以判断为队满还是队空。
缺点:需要增加额外的开销。不推荐
二)、在循环队列中少用一个数据元素,约定队尾指针加1等于对头指针表示队满。也就是牺牲一个存储空间来分辨队空还是队满。推荐
此时队满的判断条件为:
(rear+1)%queueArray.length==front
队空的判断条件为:
rear==front
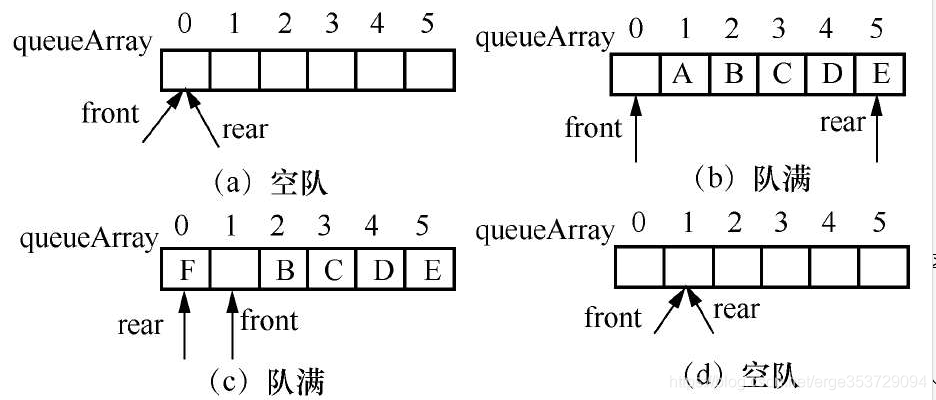
上图为循环队列队空和队满判定图
循环队列的实现
1、初始化
front=rear=0,同时初始化数组长度。
public class ArraySequenceQueue<T> implements SequenceQueue<T>{
public final static int maxSize=10;
private T[] queueArray;
private int front,rear;
public ArraySequenceQueue() {
queueArray=(T[])new Object[maxSize];
front=rear=0;
}
public ArraySequenceQueue(int n){
queueArray=(T[])new Object[n];
front=rear=0;
}2、插入
首先判断是否队满,队满,对数组进行扩容,其把队尾指针rear向后移动一位,队头指针固定不变。最后,把数据元素插入rear针指指向的位置
public void enQueue(T obj) {
//如果队满,对队列进行扩容
if((rear+1)%queueArray.length==front){
T[] p=(T[])new Object[queueArray.length*2];
if(rear==queueArray.length-1){
for(int i=1;i<=rear;i++){
p[i]=queueArray[i];
}
}else{
int j=1;
for(int i=front+1;i<queueArray.length;i++,j++){
p[j]=queueArray[i];
}
for(int i=0;i<=rear;i++,j++){
p[j]=queueArray[i];
}
front=0;
rear=queueArray.length-1;
}
queueArray=p;
}
//把rear指针往后移动一位
rear=(rear+1)%queueArray.length;
//把数据元素插入数组当中
queueArray[rear]=obj;
}上述代码的难点在于对数组进行扩容。如何把原数组中的值复制给新扩容的数组。队满的情况有两种:
1、队尾指针rear==queueArray.length-1;如下图
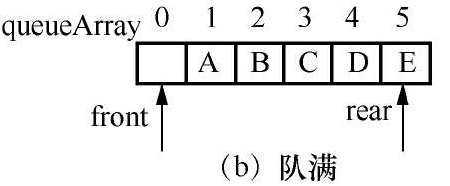
这种情况:就是把原数组中数据元素依次复制到新数组的对应的索引位置即可
2、队尾指针rear!=queueArray.length-1;如下图
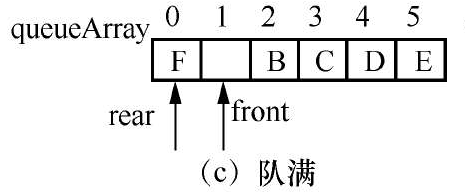
循环队列中,front指针指向存储位置为空,是当rear==front时,队空还是队满。所以拷贝数据的时候需要从front指针的后一个存储位置开始。算法如下
- 把原数组front指针后一个元素开始,到队尾,依次拷贝到新数组中,新数组存储数据元素从索引为1的位置开始
- 再把原数组中从索引0开始到指针rear所指存储位置的数据元素依次拷贝到新增组已存储数据元素的位置之后
- 重置front指针和rear指针的值,front=0,rear=queueArray.lenght-1
3、删除
首先判断是否队空,队空无法进行删除操作。然后指针front往后移动一位,队尾指针rear位置不变。最后,移除并返回队头的数据元素
public T delQueue() {
//队空,
if(rear==front){
System.out.println("队空,无法进行删除操作");
return null;
}
//front指针往后移动一位
front=(front+1)%queueArray.length;
//移除并返回对头数据元素
T delEle=queueArray[front];
queueArray[front]=null;
return delEle;
}4、获取对头数据元素
首先判空,其次返回对头数据元素
public T getHead() {
//队空,
if(rear==front){
System.out.println("队空,无法进行获取操作");
return null;
}
//返回对头数据元素
return queueArray[(front+1)%queueArray.length];
}5、求长度
public int size() {
return (rear-front+queueArray.length)%queueArray.length;
}6、判空
public boolean isEmpty() {
return rear==front;
}7、正序遍历
从对头开始,依次输出数据元素
public void nextOrder() {
int j=front;
for (int i=1;i<=size();i++){
j=(j+1)%queueArray.length; //从front指针开始,依次获取数据元素所在索引
System.out.print(queueArray[j]+" ");
}
System.out.println();
}8、销毁
public void clear() {
front=rear=0;
queueArray=null;
}链队列
用链表表示的队列称为链队列。链队列不存在假溢出的情况。链列表操作示意图如下:
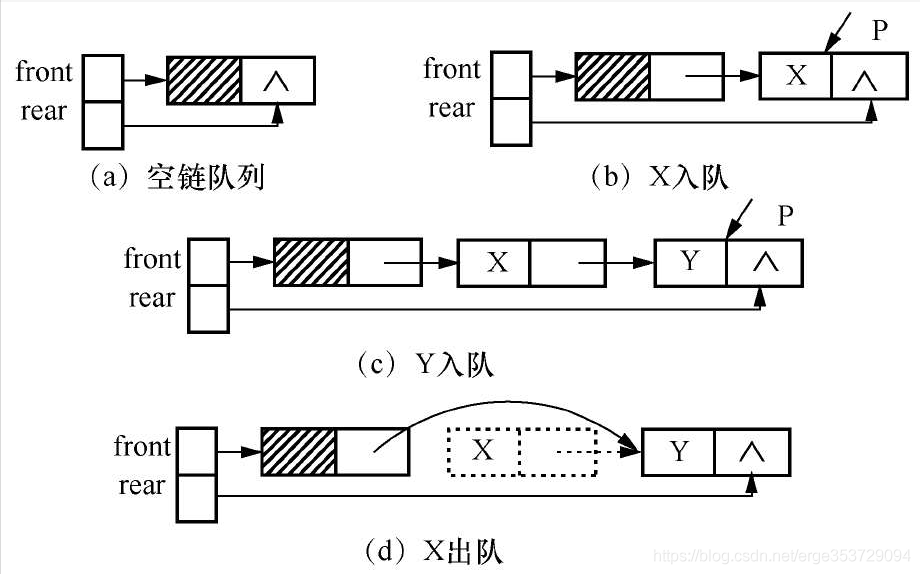
上图所示操作,front指针始终指向头节点,不从改变,所以进行出队操作时,是front.next==front.next.next。而不是front=front.next。当队空时,需要重新设置rear指针指向头节点,即rear=front;而进行入队操作时,rear指针依次往后移动一位,即rear=rear.next=p(p为新入队的数据元素),队空的判断条件为front.next==null。
public class LinkedSequenceQueue<T> implements SequenceQueue<T> {
private Node<T> front,rear;
private int length;
public LinkedSequenceQueue() {
front=rear=new Node<T>(null);
length=0;
}
class Node<T>{
T obj;
Node<T> next;
public Node(T obj, Node<T> next) {
this.obj = obj;
this.next = next;
}
public Node(T obj) {
this.obj = obj;
this.next = null;
}
}
//入队
@Override
public void enQueue(T obj) {
rear.next=new Node<T>(obj);
rear=rear.next;
length++;
}
//出队
@Override
public T delQueue() {
if(isEmpty()){
System.out.println("空对列,无法进行删除操作");
}
Node<T> p=front.next;
T data=p.obj;
front.next=p.next;
length--;
if(front.next==null){
rear=front;
}
return data;
}
//获取对头数据元素
@Override
public T getHead() {
if(isEmpty()){
System.out.println("空对列,无法进行删除操作");
}
return front.next.obj;
}
//获取元素个数
@Override
public int size() {
return length;
}
//判空
@Override
public boolean isEmpty() {
return front.next==null;
}
//正序遍历
@Override
public void nextOrder() {
Node<T> p=front.next;
while (p!=null){
System.out.print(p.obj+" ");
p=p.next;
}
System.out.println();
}
//销毁
@Override
public void clear() {
front.next=rear.next=null;
}
public static void main(String[] args) {
LinkedSequenceQueue queue=new LinkedSequenceQueue();
queue.enQueue("刘邦");
queue.enQueue("张良");
queue.enQueue("萧何");
queue.enQueue("韩信");
queue.nextOrder();
queue.delQueue();
queue.nextOrder();
}
}