分治算法基本介绍

分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)

分治算法的基本步骤

分治法在每一层递归上都有三个步骤：

1. 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题。
2. 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题。
3. 合并：将各个子问题的解合并为原问题的解。

汉诺塔—分治思想

将A全部移动到C，一次只能移动一个， 且大的盘子不能在小的上面。

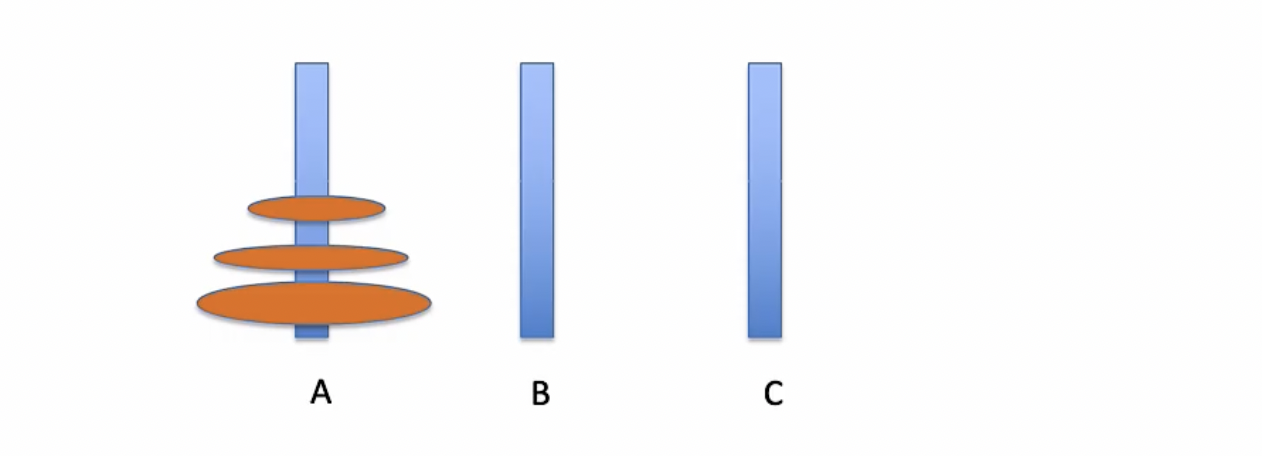
• 想象只有一个盘子就是从A到C
• 如果两个盘子先A到B、再A到C、再B到C
• 如果三个盘子先把两个移动到B、再把最大的移动到C、再把B上的两个移动到C

以三个盘子为例：

第一步 ： 将A上的俩个盘子借助C移动到B上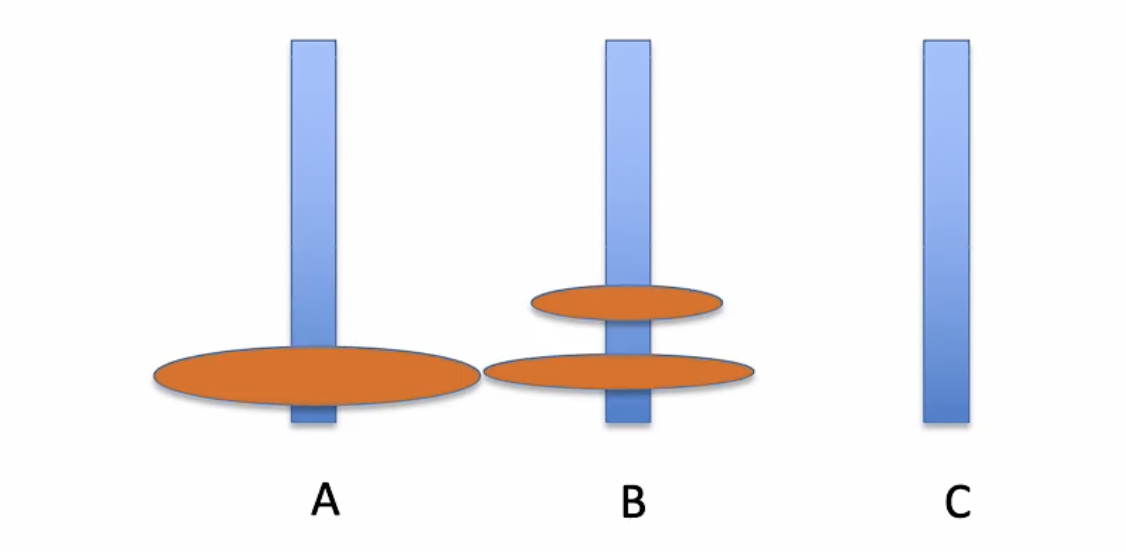

第二步：将A上的一个盘子移动到C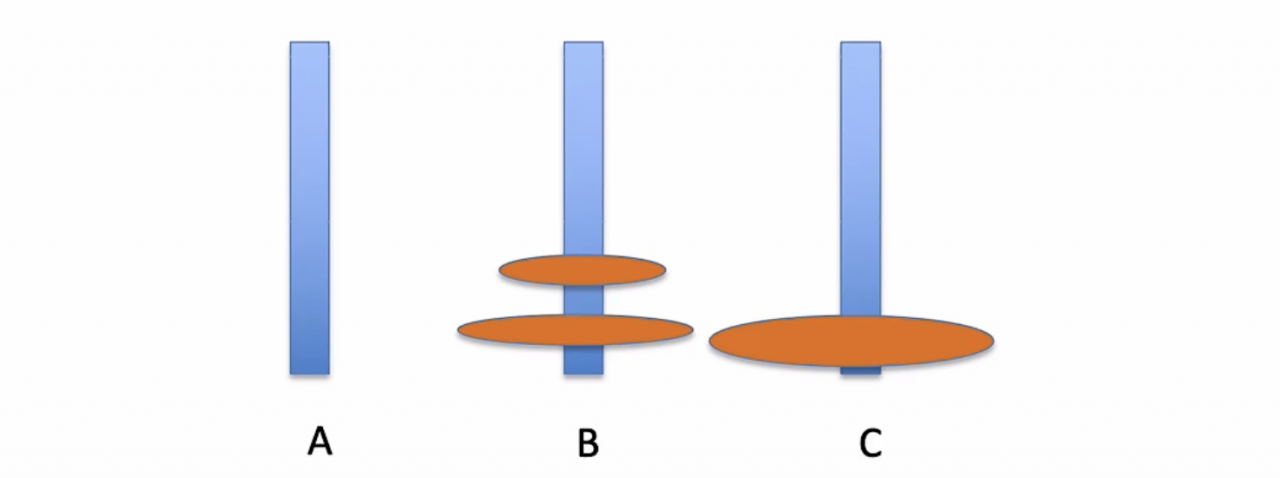

第三步：将B上的俩个盘子借助A移动到C上

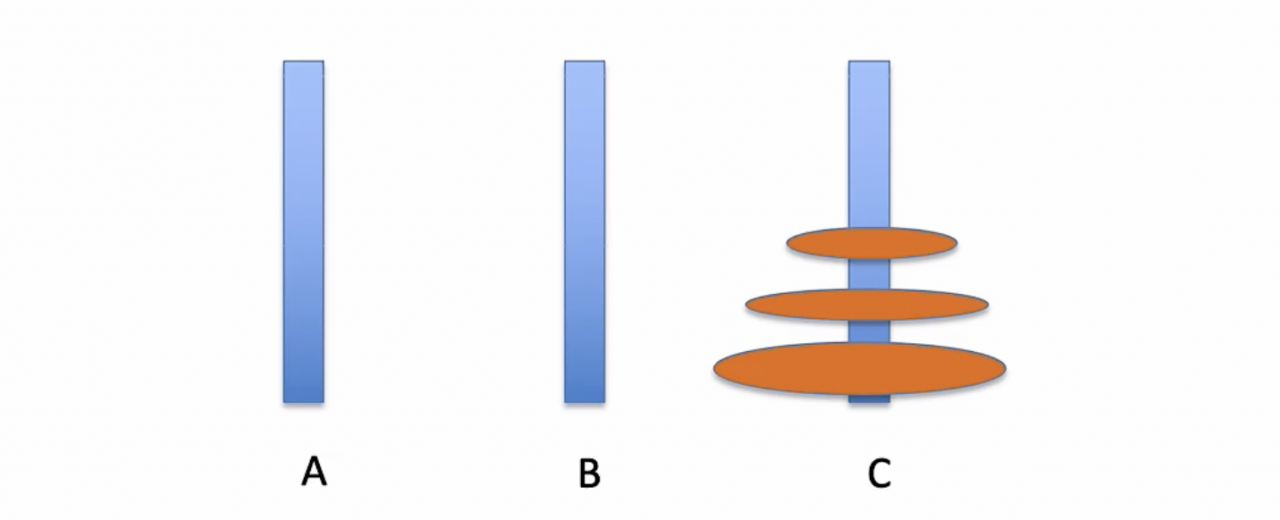
可以总结出规律

• 如果是有一个盘， A->C (就一步骤， A 移动到 C)
• 如果我们有 n >= 2 个盘的情况，我们总是可以看做是两部分盘 【1、最下边的一个盘 ，2、上面的所有盘】
  • 先把最上面的盘 A->B
  • 把最下边的盘 A->C
  • 把B塔的所有盘 从 B->C

分治算法，划分子问题。子问题需要和父问题具有相同的性质。

父问题(A,C)拆分成子问题

伪代码：

汉诺塔—代码实现

/**
 * @ClassName HanoiTower
 * @author: shouanzh
 * @Description 汉诺塔(分治算法)
 * @date 2022/5/23 20:01
 */
public class HanoiTower {

    public static void main(String[] args) {
        hanoiTower('X', 'Y', 'Z',3);
    }


    /**
     * 汉诺塔(分治算法)
     * @param x   第一根柱子 x
     * @param y   第二根柱子 y
     * @param z   第三根柱子 z
     * @param num 圆盘数量
     * x、y、z 还可以理解为：x挪到z上去,通过y
     */
    public static void hanoiTower(char x, char y, char z, int num) {

        // 如果是有一个盘， X->Z (就一步, X 移动到 Z)
        if (num == 1) {
            move(x, z);
        } else {
            // 如果我们有 num >= 2 情况, 我们总是可以看做是两部分 【1.最下边的一个盘, 2. 上面的所有盘】
            // 1、将n-1个盘子由X经过Z移动到Y
            // 传参: x,y,z 后俩个交换位置 x,z,y  方便记忆
            hanoiTower(x, z, y, num - 1);
            // 2、移动最下边的盘 X->Z
            move(x, z);
            // 3、剩下的n-1盘子由Y经过X移动到Z
            // 传参: x,y,z 前俩个交换位置 y,x,z  方便记忆
            hanoiTower(y, x, z, num - 1);
        }

    }

    /**
     * 移动
     */
    private static void move(char x, char z) {
        System.out.println("move: " + x + "--->" + z);
    }

}

三个盘子的移动步骤

move: X--->Z
move: X--->Y
move: Z--->Y
move: X--->Z
move: Y--->X
move: Y--->Z
move: X--->Z

人工递归过程

?