AES(Advanced Encryption Standard)密码学中的高级加密标准,又称Rijndael加密法,是美国联邦政府采用的一种区块加密标准。该算法为比利时密码学家Joan Daemen和Vincent Rijmen所设计,结合两位作者的名字,以Rijdael之名命之。
特点:
- 针对差分分析和线性分析而提出来的
- 具有128位数据分组长度和可变密钥长度128、192、256位
- 属于分组密码,不是Feistel结构而是SP结构
- 非对合运算:加密解密采用不同算法
- 综合运用了置换、代替、代数等多种密码技术
一、数学基础
在AES中选择的是不可约多项式p(x)=x^8+x^4+x^3+x+1,余式的次数最多是7次,共2^8=256个多项式;字节b用二进制表示为![]() ;若用多项式表示:
;若用多项式表示:![]()
![]() ,例如:字节 '57' (16进制)对应二进制为01010111,所以其对应的多项式应为:
,例如:字节 '57' (16进制)对应二进制为01010111,所以其对应的多项式应为:![]()
加法操作
两数相加为模2加即异或操作,例如 '57' + '83' = 'D4',多项式表示为:![]()
mod p(x)是在超出![]() 7次幂的情况下模一个p(x)
7次幂的情况下模一个p(x)
二进制表示为:![]()
乘法操作
8次不可约多项式确定为:![]() ,其十六进制表示为 '11B'
,其十六进制表示为 '11B'
例如:'57' * ’83‘ = ’C1' 用多项式表示为:![]() 即:
即:![]() 结果为:
结果为: ![]() 很明显结果超出了7次幂,所以应该用结果模一个p(x),且注意p(x)最高位应与结果最高位相等,所以p(x)应乘以一个相应的
很明显结果超出了7次幂,所以应该用结果模一个p(x),且注意p(x)最高位应与结果最高位相等,所以p(x)应乘以一个相应的![]() ,即:
,即:![]() ,将其与结果进行异或操作得
,将其与结果进行异或操作得![]() ;该结果还是超出了7次幂,所应该再次循环上一步,模一个p(x),但此时的p(x)最高位同样应与结果相等,即:
;该结果还是超出了7次幂,所应该再次循环上一步,模一个p(x),但此时的p(x)最高位同样应与结果相等,即:![]() ,将其与结果再次进行异或操作得
,将其与结果再次进行异或操作得![]() ;该结果最高次幂未超出7次,所以这就是最终结果。
;该结果最高次幂未超出7次,所以这就是最终结果。
乘法逆元
求次数小于8的非零多项式b(x)的乘法逆元,需通过扩展欧几里得算法求得a(x)和c(x),使得b(x)a(x)+p(x)c(x)=1,a(x)即为b(x)的乘法逆元。
例如:
F5 用二进制表示为:11110101,用多项式表示为![]() ,计算两个多项式a(x)和c(x),需满足
,计算两个多项式a(x)和c(x),需满足![]()
![]() ;采用多项式的扩展欧几里得算法按如下步骤计算
;采用多项式的扩展欧几里得算法按如下步骤计算![]()
![]()
两式化简后得:
![]()
![]() 这里的
这里的![]() 即为b(x)的乘法逆元。
即为b(x)的乘法逆元。
二、加密过程
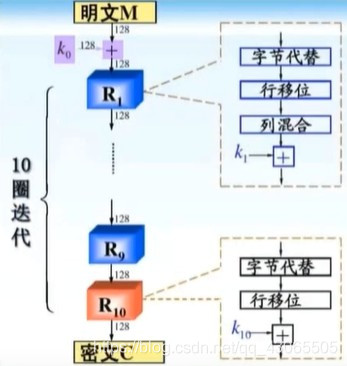
加密过程与DES类似,只是有部分不同。
AES将明文划分未4行Nb列的数据,Nb为明文数据长度,即数据块长度除以32(4*8),Nk为密钥数据长度(同Nb);
S盒操作
在S盒部分,AES使用16个相同的S盒,均为8进8出;DES使用了8个不同的S盒,均为6进4出。原理:将输入的高4位作为行数,低4位作为列数,查S盒表如下图;例如:输入95,查找9行5列的数,输出2a。
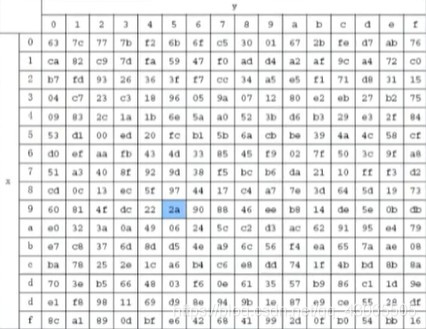
直接查表可以得出,同样也可以通过计算的方法,原理:先计算输入字节的乘法逆元,将乘法逆元乘以如下矩阵再与01100011做异或运算,如:输入数据95,其乘法逆元为8a,二进制表示为10001010,进行计算后得出结果00101010,16进制表示为2a。

行移位
第0行循环左移0位,第1行循环左移1位,第2行循环左移2位,第3行循环左移3位;
列混合
将行移位后的矩阵乘以一个矩阵得到列混合后的结果(这里所有的加法均为![]() 异或运算,包括矩阵的计算)。
异或运算,包括矩阵的计算)。

轮密钥加
将进行列混合后的数据(4*4)与密钥(4*4)进行对位模2加(异或)
轮密钥的产生
设初始密钥为2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C,则K0={W0,W1,W2,W3}
| W0 | W1 | W2 | W3 |
|---|---|---|---|
| 2B | 28 | AB | 09 |
| 7E | AE | F7 | CF |
| 15 | D2 | 15 | 4F |
| 16 | A6 | 88 | 3C |
K1={W4,W5,W6,W7},K2、K3、K4......同理,当i≥4时,![]()