这两部分都是对残差假设的检验,经典回归模型的残差服从(0,
library(ggplot2)
library(foreign)
data5.1<-read.dta("case 5-1.dta")
View(data5.1)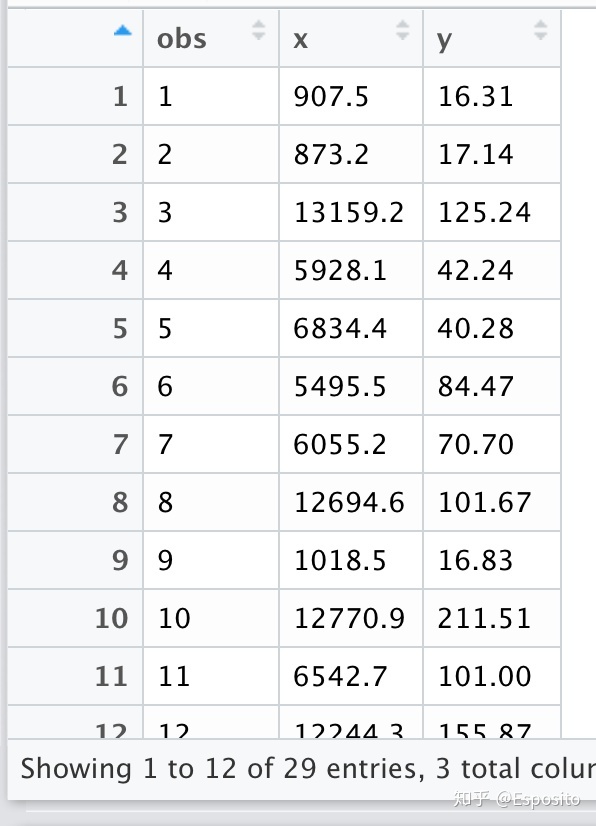
给出数据的部分截图
一元拟合还是习惯先用ggplot2看下效果图。
p<-ggplot(data = data5.1,aes(x,y))
p+geom_point(colour="black",shape=3)+
geom_smooth(method = "lm",colour="black",level=0.95)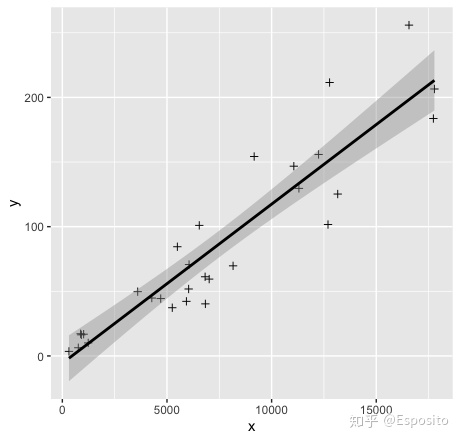
这里看到散的分布会随x的增大而更加分散,接下来我们看下拟合的残差与x的散点图。
lm1<-lm(y~x,data=data5.1)#回归
e<-resid(lm1)#获取残差
data.resid<-data.frame(data5.1[,2],e)#残差与x合并
ggplot(data = data.resid,aes(x,e))+
geom_point()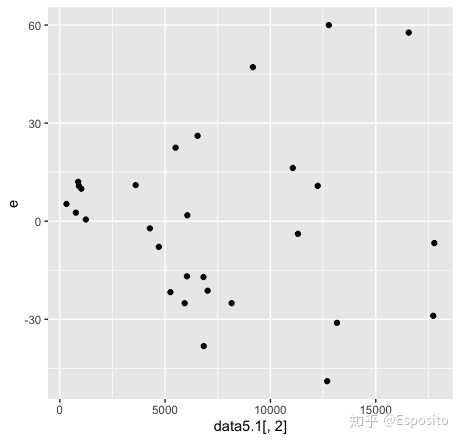
可以很明显看到残差随着x的增大更加分散。
这里还给出white检验和H.glejser检验
#white检验,p小于显著性则拒绝不具有异方差假设
x<-data5.1[,2]
fm<-lm(I(e^2)~x+I(x^2))
R<-summary(fm)$r.sq
n=nrow(fm$model)
m=ncol(fm$model)
W=n*R
p=1-pchisq(W,m-1)
data.frame(W,p)white检验做一个辅助函数,让拟合的残差与x和x的平方进行拟合,构建卡方统计量。r语言里最好用I(x^2),不然它会以为就是x。

这里W对应的p值小于0.05,则拒绝原假设,接受具有异方差。
接下来是glejser检验,是残差的绝对值与解释变量的各种形式拟合,比如x,x的平方,x开方这种,看拟合效果,这里就给出残差绝对值与x 和x开方的拟合结果。
#H.glejser检验,检验残差与个解释变量的拟合
lm.g1<-lm(abs(e)~x)
lm.g2<-lm(abs(e)~sqrt(x))
summary(lm.g1)$coef
summary(lm.g2)$coef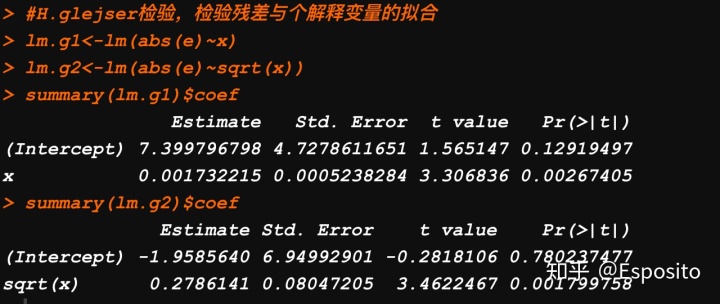
这里可以看到系数的t简言之对应的p值都小于0.05,则可以说明具有异方差。
异方差的解决,一个就是两边同时取对数,进行拟合。可以减少异方差,这里就不再过多说明了。
还有就是加权的最小二乘法,实际就是原来模型地下同时除以一个标准差。 在r里就是给一个权重,实际上模型就是乘上权重的开方。不过有的书上是除以根号下e,有的是除以根号下x,其实都是一个意思,毕竟这里x和e是相关的。
#异方差的处理方法,取对数,加权最小二乘法
lm.lg<-lm(log(y)~log(x),data=data5.1)#取对数
e<-summary(lm1)$resid
lm.weight<-lm(y~x,data=data5.1,weight=1/abs(e))#加权最小二乘法
summary(lm.weight)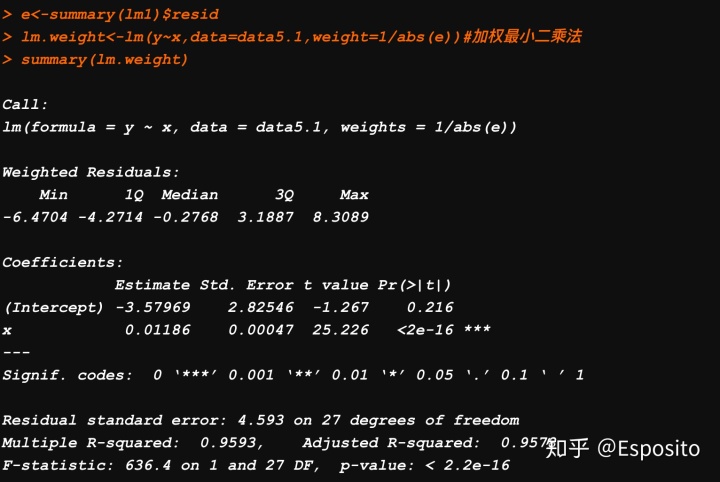
这里系数对应到公式里应该是,y/sqrt(e) = -3.579691/sqrt(e)+0.01186*x/sqrt(e).
这样异方差就能一定程度的解决了。
当然后面取对数就可以解决大部分的异方差问题了,而且操作也比较简单,可以先试试取对数的效果。