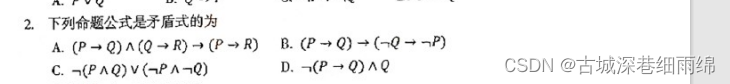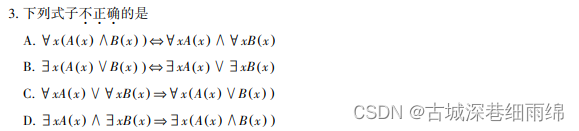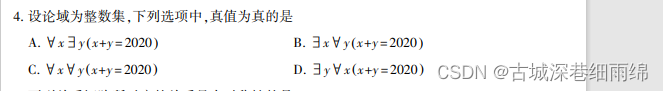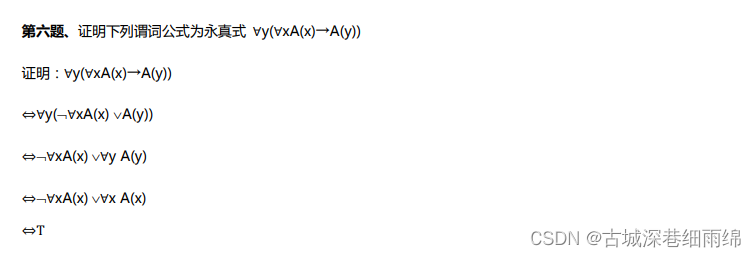第一章:命题与命题公式
(2道选择或填空,1道解答题,共8分左右)
1、选择、填空:
(1)命题符号化(每年第一题):
例:①:2021年10月:
1. 设 p:今年是 2020 年,q:明年是 2021 年,命题“只有今年是 2020 年,明年才是 2021 年的符 号化为 A. p∧q B. p∨q C. p→q D. q→p
解析:一般做这类题型搞清楚谁是谁的前提就可以,例如明年是2021年的前提是今年是2020年,所以例①选D。
(2)求一个公式的矛盾式或永真式
例:2021年4月:
解析:一般做这类题型只需用等值演算法算出就可以,也可以用假设法设其中一个值为T或F,看整个公式能不能取真,如果能,则不是矛盾式,如果不管取T或F,公式都是F,则是矛盾式。实在不会也可以用真值表法,方法还是比较多的。
用等值演算法求得D最后得公式为:P∧¬Q∧Q,为矛盾式(永假式),所以选D。
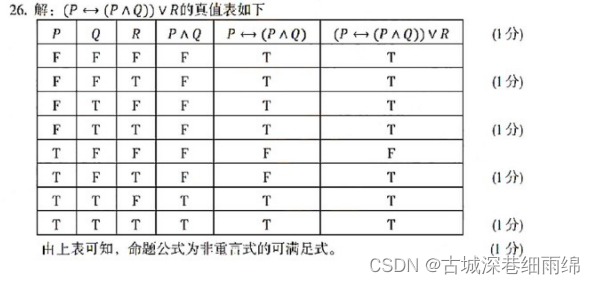
★(3)用真值表法求一个式子是否为可满足式(简答题第一题)
例:
解析:这类题一般很好拿分,只要细心一点就没问题。
(4)逻辑推导:(考的少)
例:小赵、小钱、小孙、小李参加数学建模竞赛,根据下列情况,确定 4 人中获奖的是哪些人,未获奖的是哪 些人。需写出推导过程。
(1)只要小赵或小钱中一人未获奖,小孙和小李就都得奖;
(2)小孙没获奖或小李没获奖是 不可能的;
(3)小钱获奖了。
解析:做此类题首先把命题符号化再求他们的合取,用等值演算就可求出结果
第二章: 命题逻辑的推理理论
(1道选择或填空、1道简答,1道证明 。共15分左右)
1、选择、填空:
(1)小项的性质考查:
2021年10月:
2021年4月:
解析:只需要记住小项打的的性质就可:
小项:每个小项当其真指派与编码相同时为T,其余都是F,所以任意两个小项的合取是永假,全体小项的析取为真,有2的n次方个小项。
大项:每个大项项当其真指派与编码相同时为F,其余都是T,所以任意两个大项的析取取是永真,全体小项的合取为假,有2的n次方个大项。
(2)求大小项的个数:
2020年10月:
答案:1个
2020年8月:
答案:3个
解析:用等值演算法或者真值表法求就可以求出来,看清是求主合取还是主析取。以2020年10月为例:
2、解答题:
用等值演算法求魔公式的主合取范式或者主析取范式(解答题第二题)
2021年10月:
2021年4月:
解析:考的是等追演算,把等值公式表重要的式子记住就行。适当的利用排中律和否定律添加缺少的命题。例:P、Q、R。公式里只有PVQ ,可变为PVQ(R∧¬R)。
答案:
2021年4月:
3、证明题:
逻辑推理:
2021年4月:
答案:
解析:考的是自然推理系统一节的内容,了解P规则,T规则,(归谬法)反正法:结果取反当条件拿来用,cp规则:A→B,A拿来当条件用,可根据公式A→B=¬A∨B,灵活变换。
第三章:谓词逻辑
(两道选择两道填空。大题可能出,21年20年未出。不算大题8分左右)
1、选择填空:
(1)谓词等值式和蕴含式的考查:
例:2021年10月:
解析: 由表可知D是错的,假设一个班上的同学为X。会唱歌为A(x),会跳舞为B(X),等是左边:存在一些同学会唱歌,且存在一下同学会跳舞;等式右边:存在一些同学会唱歌且会跳舞。显然是不等价的,所以选择D。
2、论域、辖域、指导变元、自由变元、约束变元的考查。
例:2021年10月:
解析:已知论域是整数:选择题,往进带值就可以。 A:对任意一个X都存在Y,使其相加=2020,A对。B:存在一个x对任意一个y,和其相加等于2020,显然是错的。c,对任意一个X都有任意一个y和其相加等于2020,错的。D:同B。
二、证明题:
例:
解析:与命题逻辑推理相似,多了4个:全称量词消去规则、全称量词引入规则(少用)、存在量词引入规则、存在量词消去规则 。
第四章:集合
(选择或填空出一道、大题可能会出证明题。21年20年未出。不算大题2分左右)
一、选择填空:
2021年10月:
解析:单位元即幺元,首先想到的是∅集。
2020年10月:
解析:
2020年8月:
解析:真子集的概念:A包含B,但A至少有一个元素不属于B。例:A={1,2,3,4},B={1,2,3} 。所以选c。
二、证明题:
解析:考查的是集合的运算公式:
第五章:关系与函数(本书重点)
(选择填空(2021年10月):12分,大题(2021年10月):12分,共24分左右)
一、考查内容:
- 关系的三种表示方法(单选)
- 关系的性质(单选、填空)
- 关系的闭包运算(单选、填空、计算)
- 关系的复合运算(单选、填空)
- 关系的判断和证明(单选、填空)
- 等价关系与划分(单选、填空)
- 序关系中的特殊元素(单选。填空、计算)
- 函数的复合(单选、填空)
二、选择填空:
2021年10月:

解析:
第5题:自反:对角线全是1;反自反:对角线全是0;对称:关于对角线对称;反对称:关于对角线两侧不能同时为1。所以5题选C。
第6题: 单射:1对1;满射:一对多;双射:既有1对1,又有一对多。所以6题的意思是,A中的元素既要和B中的1有关系,又要和B中的2有关系。故,可分为,①:A中的1个元素对应B中的1,4个元素对应B中的2;②:A中2个元素对应B中的1,3个元素对应B中的2;③:A中3个元素对应B中的1,2个元素对应B中的2;④:A中4个元素B中的对应1,1个元素对应B中的2,这四种情况。第①种有5种情况;第②种有10种情况,第③种有10种情况;第④种有5种情况,所以一共有30种情况。
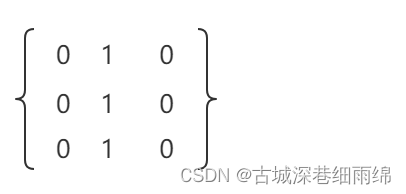
第7题:用关系矩阵画出来后如图:
自反、反自反、对称都不符合,所以选D。
第8题:等价关系包含:自反、对称、传递。如果R满足这些关系,则R的逆也满足,所以选A。记住下面这个表:
运算\性质 自反 反自反 对称 反对称 传递 R 的逆 √ √ √ √ √ R ∩ S √ √ √ √ √ R ∪ S √ √ √ × × R - S × √ √ √ × R ° S √ × × × ×

解析:
第19题:
首先S的逆={<1,3>},R∪S的逆={<1,2><1,3><2,2><3,2>},dom表示定义域,取出第一个元素,所以答案为:{1,2,3}。(ranR:值域,fldR:域)
第20题:
划分为{1,4},{2,3},等价关系是自反,对称,传递,则:<1,4>x<1,4>={<1,1>,<1,4>,<4,1>,<4,4>}, <2,3>x<2,3>={<2,2>,<2,3>,<3,2>,<3,3>},最后得答案为:{<1,1>,<1,4>,<4,1>,<4,4>,<2,2>,<2,3>,<3,2>,<3,3>}
第21题:
幂集:所有子集之和:2的n次方个,则A的幂集有16个。对称差:并集-交集。单位元:与任何一个元素做运算都等于这个元素。首先想到特殊的元素:∅和A本身。∅和A本身的对称差还是A本身,所以∅为单位元。
第22题:
Klein四元群如下:
* e a b c e e a b c a a e c b b b c e a c c b a e 书本原题:例6.13:
定义6.12:群的阶:群里元素的个数叫做阶数、
定义6.15:元素的阶:设e是群里的幺元。a是群里的元素。a的k次方=e(幺元),则k被称为k阶元。
所以除单位元外,其他元素都是各自本身的2次方等于单位元,如a²=e,b²=4,c²=e。所以阶都是2.
三、大题:
1、2021年10月:
2、题型:
第六章:代数系统
一、考查内容:
- 代数系统的三个特殊元素(单选、填空)
- 群的判断与群的性质(单选、填空、证明)
- 半群与独异点的概念(单选)
二、选择填空:
2021年10月:
2021年4月:
解析:
2021年10月:
第14题:
a○a=a,b○b=b,则满足幂等律,AD排除,a○b=b,b○a=a,显然是不满足交换律的,所以B排除,a○a○b=a○(a○b)=a○b,满足结合律,所以选C。
2021年4月:
第7题:
与上面的14题相似,a○a=a,b○b≠b,所以不满足幂等律,是座椅选B
第14题:
群的性质:封闭性,结合律,幺元、逆元。自然数加法运算中没有a+a'=0的数,所以A错。
第19题:

三、大题:
2021年10月:
2021年4月:
答案:
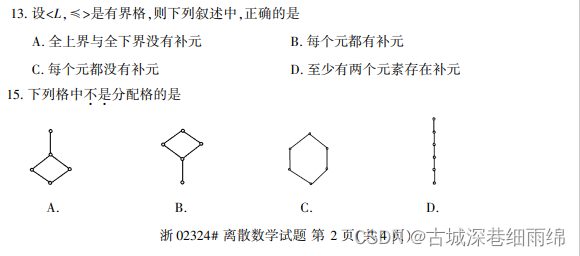
第七章:格与布尔代数
一、考查内容:
- 格中元素的补元(单选、填空)
- 格的判断
二、选择填空:
2021年10月:
2021年4月:
解析:
2021年10月:
第13题:
有界格:有上确界和下确界。书本定义7.10:在任何有界格中全上界和全下界总是互补的,而对于其他元素,可能2存在补元也可能不存在补元。所以选D,至少有两个,分别是上确界和下确界。
第15题:
分配格:不含有钻石格和五角格。显然C不是,因为五角格是六角格的子格。
2021年4月:
第15题:
补格:相∪=1,相交=0,所以c的补元是a。
第八章:图(8分左右,会出一道大题)
一、选择填空:
1、可简单图化:
2020年10月:
2021年4月:
解析:以2021年4月的题为例:可简单图化需满足两个条件:①:节点读书最多为n-1个(n为点的个数,如A有5个,B有6个,c有4个,D有4个),所以AD排除,②:点的个数不能为奇数(例如:B:3+3+2+2+1+1=12,C:3+3+3+1=10,都满足。③依次删除首元素,首元素后的元素-1,重复以上步骤,直至最后一个元素为0(例如:B:除去3 ,后面的数字为2,1,1,0,0,0舍去,继续去掉2,后面的数字为0,0.B可以。C:去掉3,后面的数字为2,2,0,0舍去。继续去掉2,后面的数字为1。最后得到的数字是1,所以不行)所以选择B选项。
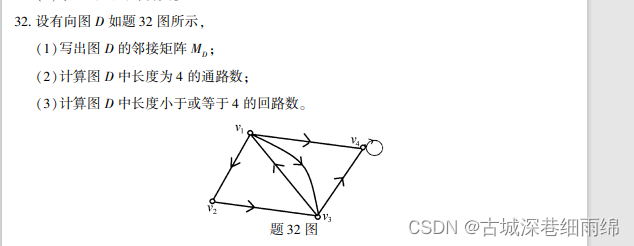
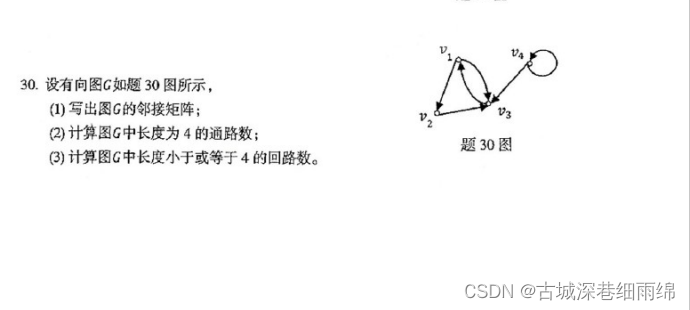
二、大题:
2021年10月:
2021年4月:
答案:
解析:邻接矩阵算法:(1)以第一行第三列的数为例:
通路:所有的数加起来。
回路:左斜对角的数加起来(第一行第一列、第二行第二例、第三行第三列。。。。)
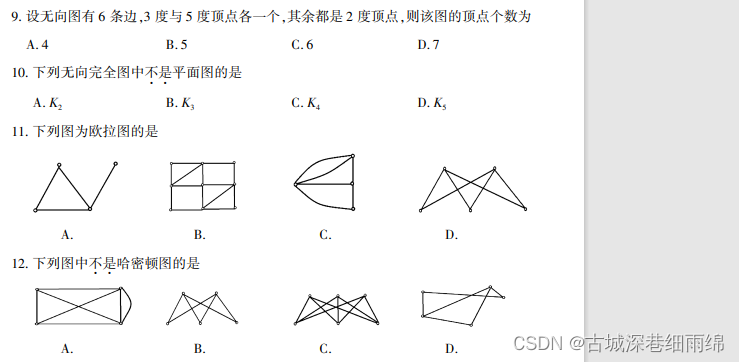
第九章:图的应用(26分左右)
1、选择填空:
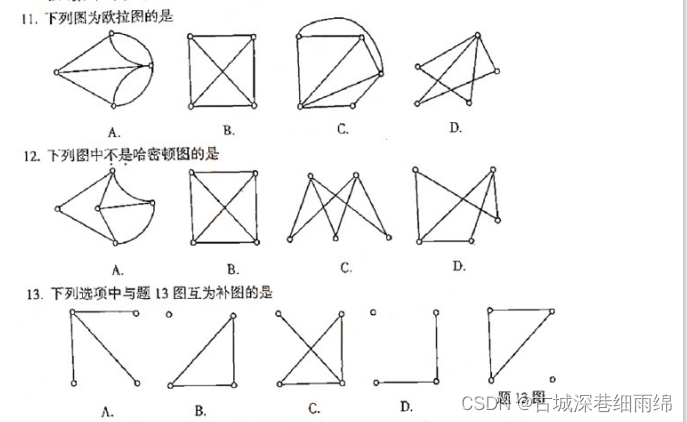
考查图的性质:包括平面图、欧拉图、哈密顿图、欧拉定理、握手定理
2021年10月:
2021年4月:
2、大题:
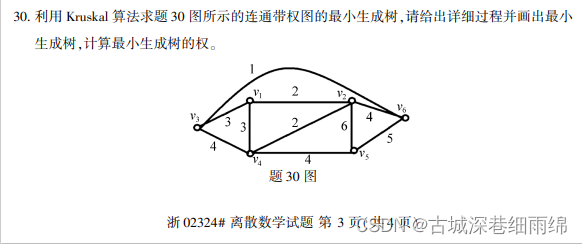
最小生成树的考查、二叉树的遍历:
2021年10月:
2021年4月: