高斯函数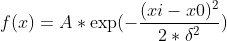： $f(x)=A\exp (-\frac{(xi-x0)^{2}}{2\delta ^{2}})$

已知一组数据：Yi={x1，x2,...,xn}，需要拟合成高斯函数。

令 F（x）=lnf(x), $F(x)=lnA-\frac{(xi-x0)^{2}}{2*\delta ^{2}}$ ,化简可得到式（1），

F(x)=lnA-x0^2/2*simga^2+xi*x0/sigma^2-xi^2/2*sigma^2.......................................................................................................（1）

令 a0=lnA-x0^2/2*simga^2，a1=x0/sigma^2,a2=-1/2*sigma^2,则F（x）可化为一个二项式,式（2）

F（x）=a0+a1*x+a2*x^2.........................................................................................................................................................（2）

高斯转为二次曲线，但是如何进行拟合？

拟合的思想就是求一条曲线，让所有数据点都接近该曲线。如何判断都接近呢？

我们可以假设拟合的二次曲线是已知的，利用原有数据点和拟合数据点之间的距离列方程，通过计算该最小距离方程，即可求出假设的拟合曲线的参数。如式（2），在求的过程中，x是已知的，a0，a1，a2是曲线的形状设置的未知参数，也就是需要求解的参数。我们通过已知的已知一组数据Yi，分别带入高斯函数，能得到一组f（x）和对应的F（x），此时的F（x）就是拟合出来的结果，因此距离方程为公式（3），即利用最小二乘法拟合曲线。

$M=\sum [Yi-a0+a1\cdot x+a2\cdot x^{2}]^{2}$ .........................................................................................................................（3）

最后转为求公式（3）[a0,a1,a2]的解。分别对a0，a1，a2求偏导数，并整理。 $M=\sum [Yi-a0+a1\cdot x+a2\cdot x^{2}]^{2}$

最后，可通过豪斯霍尔德变换求方程解[a0,a1,a2]。高斯函数的极值为：Xc=-a1/2a2

原文链接：https://blog.csdn.net/Abaqus3_0/article/details/82011159