11决策树算法；12案例实战：使用sklearn构造决策树模型（含数据）

唐宇迪《python数据分析与机器学习实战》学习笔记
11决策树算法

文章目录

第一部分：算法

1.1 算法概述

例如：将家里人分类，可以先分年龄再分性别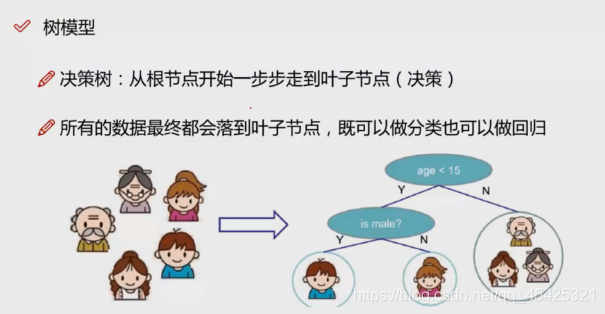
在这里插入图片描述
决策树组成:根节点，非叶子节点与分支，叶子节点。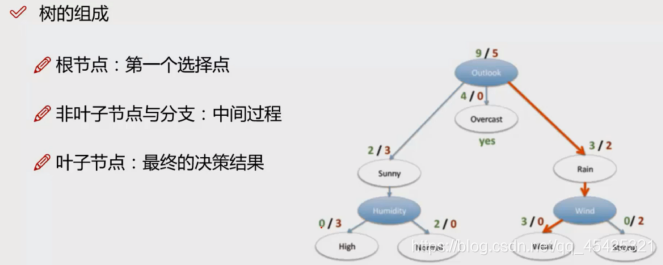
在这里插入图片描述
越多的特征越多的节点，每多一个特征，深度越深
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

1.2 特征选择顺序的衡量标准-熵值

在这里插入图片描述
信息增益率: = H(X前) - H(X后),以某特征划分数据集前后的熵的差值
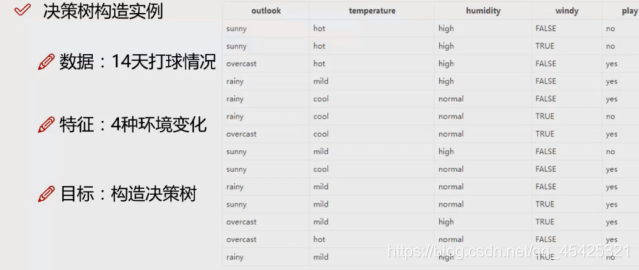
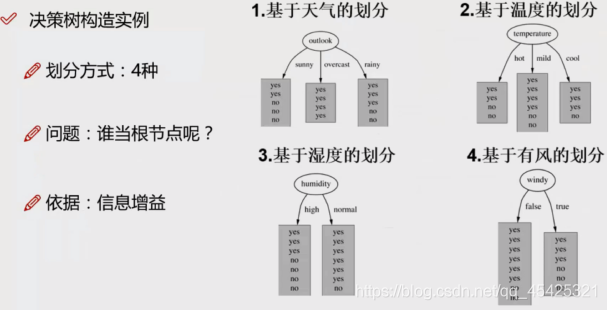
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
选择信息增益率最大的为根节点
在这里插入图片描述
GINI系数

表示在样本集合中一个随机选中的样本被分错的概率,Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯.样本被选中的概率 * 样本被分错的概率
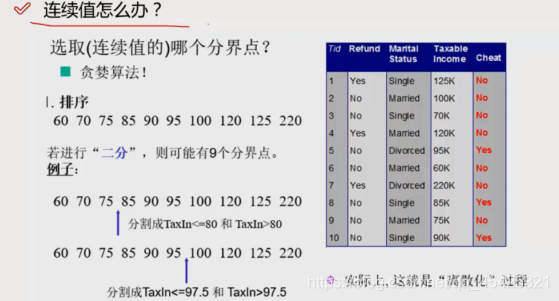
在这里插入图片描述
在这里插入图片描述

1.3 决策树减枝策略

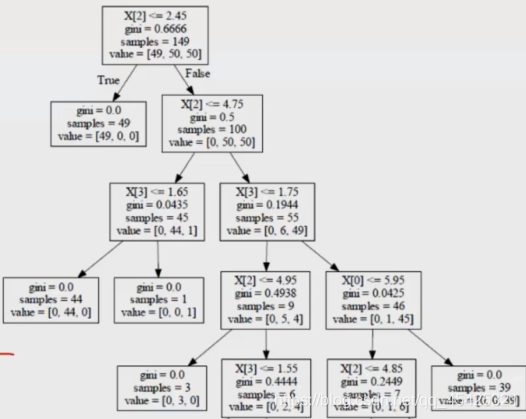
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
Cα（T）“母节点”的叶子节点数熵值或GINI系数，C(T)表示当前的损失（叶子节点数熵值或GINI系数，然后所有叶子累加），后部分限制叶子节点个数。 比较等号两边，越小越好看是否切掉。以上图左侧倒数第二排的X[0]为例：不切就是【0.042546+α】，切了就是【70.2449+39*0+2α】，通过设定α来决定是否减。

第二部分:简单案例

2.1 数据导入及查看

导入库

%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd

从sklearn中导入模块，里面包含一些内置的数据集，这里导入某地区房价（包含一些影响房价的因素），这里主要是想用这些因素去预测房价，具体特征如下所示。

from sklearn.datasets.california_housing import fetch_california_housing
housing = fetch_california_housing()
print(housing.DESCR)

在这里插入图片描述
数据观察

housing.data.shape

(20640, 8)

housing.data[0]

array([ 8.3252 , 41. , 6.98412698, 1.02380952, 322. , 2.55555556, 37.88 , -122.23 ])

2.2 决策树建立、展示及预测

2.2.1 训练决策树

这里只用里面的**经度纬度（Latitude，Longitude）**信息来预测
从sklearn里面导入tree模块，进行分类也可以，进行回归也可以。

from sklearn import tree
dtr = tree.DecisionTreeRegressor(max_depth=2)  #控制深度
dtr.fit(housing.data[:,[6,7]],housing.target)  #传入经纬度做x特征，房价作y标签

这里扩展一下决策树的参数：
（1）criterion gini or entropy 基尼系数/熵值，
（2）splitter best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中（数据量大的时候）默认best
（3）max_features： None（所有），log2，sqrt，N。特征小于50的时候一般使用所有的特征
（4） max_depth 数据少或者特征少的时候可以不管这个值，如果模型样本量多，特征也多的情况下，可以尝试限制下这个决策树的深度。可以尝试遍历max_depth找出最佳。（最常用参数之一）
（5） min_samples_split 如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。（最常用参数之一） 控制叶子节点分裂情况，防过拟合。
（6）min_samples_leaf 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝，如果样本量不大，不需要管这个值，大些如10W可是尝试下
（7）min_weight_fraction_leaf 这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
（8）max_leaf_nodes 通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制具体的值可以通过交叉验证得到。
（9）class_weight 指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重如果使用“balanced”，则算法会自己计算权重，样本量少的类别所对应的样本权重会高。
（10）min_impurity_split 这个值限制了决策树的增长，如果某节点的不纯度(基尼系数，信息增益，均方差，绝对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。
（11）n_estimators:要建立树的个数，在使用随机森林时用
这些参数都是用来剪枝决策树，防止决策树太过庞大或者出现过拟合的现象。

2.2.2 决策树可视化（pydotplus）

先下载可视化软件Grahviz：下载地址（下载msi文件）；安装流程 。（备注：用pip安装后面会报错，所以还是老老实实下载安装，然后将bin目录路径环境变量path下）
接着进行决策树可视化，先生成idot文件：

dot_data = \
    tree.export_graphviz(
    dtr,  #需指定树名
    out_file = None,
    feature_names = housing.feature_names[6:8], #需指定特征名
    filled = True,
    impurity = False,
    rounded = True
    )

进行可视化：

#安装一下：pip install pydotplus
import pydotplus
graph = pydotplus.graph_from_dot_data(dot_data)  #传数据
graph.get_nodes()[7].set_fillcolor("#FFF2DD")    #改颜色
from IPython.display import Image
Image(graph.create_png())

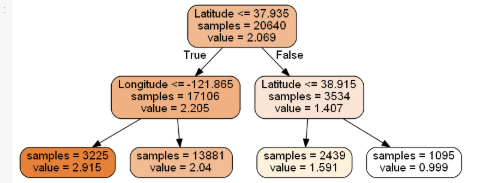
在这里插入图片描述
然后保存图片为（png格式比较清晰）：

graph.write_png('dtr_white_background.png')

2.2.3 预测及效果

决策树数据集切分（训练集＋测试集）、训练、预测及效果

from sklearn.model_selection import train_test_split
#90%为训练集，10%作为测试集
data_train, data_test, target_train, target_test = \
    train_test_split(housing.data, housing.target, test_size = 0.1, random_state = 42)
    #random_state 随机复现，保持每次随机结果一致
dtr = tree.DecisionTreeRegressor(random_state = 42)
dtr.fit(data_train, target_train)  #传入数据
dtr.score(data_test, target_test)

0.637355881715626
备注：http://scikit_learn.org/stable/ 可以官网看一下用法,特别是eaxmple

随机森林建立

from sklearn.ensemble import RandomForestRegressor
rfr = RandomForestRegressor(random_state = 42) #默认建立10棵树
rfr.fit(data_train, target_train)
rfr.score(data_test, target_test)

0.8097021394052101

2.3 Sklearn参数选择问题（GridSearchCV）

使用grid_search 遍历参数，看哪些参数组合效果最佳

from sklearn.model_selection import learning_curve, GridSearchCV
tree_param_grid = {'min_samples_split': list((3,6,9)),'n_estimators':list((10,50,100))}#建立参数字典
#参数1：最少分裂叶子节点；参数2：树木数量
grid = GridSearchCV(RandomForestRegressor(),param_grid=tree_param_grid, cv=5)
#算法；参数候选项（字典格式）；cv代表交叉验证次数
grid.fit(data_train, target_train)
grid.cv_results_, grid.best_params_, grid.best_score_
#得分值；最好参数；最好得分

({‘mean_fit_time’: array([1.00125718, 4.97068424, 9.95776954, 0.91525235, 4.64746585,
9.22172747, 0.87905035, 4.40465198, 8.89970899]),
‘std_fit_time’: array([0.01566476, 0.02599832, 0.07968249, 0.01987474, 0.10681515,
0.07381857, 0.01035427, 0.08436977, 0.08677226]),
‘mean_score_time’: array([0.01260076, 0.05400314, 0.10460601, 0.00980053, 0.04500251,
0.08860502, 0.00920053, 0.0406023 , 0.08160472]),
‘std_score_time’: array([0.00174365, 0.00200016, 0.00313711, 0.00040011, 0.00200005,
0.00101996, 0.00074834, 0.00101987, 0.00048988]),
‘param_min_samples_split’: masked_array(data=[3, 3, 3, 6, 6, 6, 9, 9, 9],
mask=[False, False, False, False, False, False, False, False,
False],
fill_value=’?’,
dtype=object),
‘param_n_estimators’: masked_array(data=[10, 50, 100, 10, 50, 100, 10, 50, 100],
mask=[False, False, False, False, False, False, False, False,
False],
fill_value=’?’,
dtype=object),
‘params’: [{‘min_samples_split’: 3, ‘n_estimators’: 10},
{‘min_samples_split’: 3, ‘n_estimators’: 50},
{‘min_samples_split’: 3, ‘n_estimators’: 100},
{‘min_samples_split’: 6, ‘n_estimators’: 10},
{‘min_samples_split’: 6, ‘n_estimators’: 50},
{‘min_samples_split’: 6, ‘n_estimators’: 100},
{‘min_samples_split’: 9, ‘n_estimators’: 10},
{‘min_samples_split’: 9, ‘n_estimators’: 50},
{‘min_samples_split’: 9, ‘n_estimators’: 100}],
‘split0_test_score’: array([0.79267199, 0.80905298, 0.81068843, 0.79308882, 0.80660331,
0.80917339, 0.79162112, 0.81057495, 0.80921164]),
‘split1_test_score’: array([0.78181266, 0.80153549, 0.80103816, 0.78720601, 0.79580325,
0.80102753, 0.77912002, 0.79694886, 0.79778519]),
‘split2_test_score’: array([0.78348457, 0.79872457, 0.80435052, 0.78517225, 0.80026929,
0.80613964, 0.78861179, 0.80170534, 0.80183215]),
‘split3_test_score’: array([0.79113388, 0.81075521, 0.81157084, 0.78988706, 0.8065356 ,
0.81100536, 0.78440473, 0.80949228, 0.81104697]),
‘split4_test_score’: array([0.79603817, 0.80240321, 0.8089435 , 0.79068732, 0.80665573,
0.80721082, 0.7882916 , 0.80397085, 0.80825111]),
‘mean_test_score’: array([0.78902826, 0.80449429, 0.80731829, 0.78920829, 0.80317343,
0.80691135, 0.78640985, 0.80453846, 0.80562541]),
‘std_test_score’: array([0.00547077, 0.00461297, 0.00400827, 0.00275701, 0.00442602,
0.00338178, 0.00430602, 0.00503846, 0.00500013]),
‘rank_test_score’: array([8, 5, 1, 7, 6, 2, 9, 4, 3])},
{‘min_samples_split’: 3, ‘n_estimators’: 100},#最佳参数
0.8073182909694573)

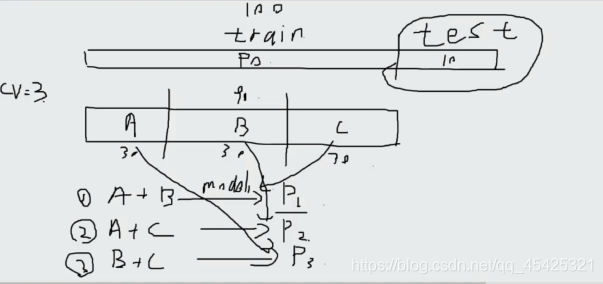
补充：交叉验证
例如将训练集切割为3份，A+B建模C测试，A+C建模B验证…,3次后取精度（P1+P2+P3）/3

在这里插入图片描述
最佳参数建模

rfr = RandomForestRegressor(min_samples_split = 3,n_estimators = 100, random_state = 42)
rfr.fit(data_train, target_train)
rfr.score(data_test, target_test)

0.8088623476993486

特征重要性展示

pd.Series(rfr.feature_importances_,index = housing.feature_names).sort_values(ascending = False)

MedInc 0.524257
AveOccup 0.137947
Latitude 0.090622
Longitude 0.089414
HouseAge 0.053970
AveRooms 0.044443
Population 0.030263
AveBedrms 0.029084
dtype: float64

版权声明：本文为qq_45425321原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。