机器学习及相关模型简介

机器学习是一门多领域交叉的学科，是人工智能的基础。利用大量的数据进行分析与挖掘，机器学习的模型作为一种从数据当中发现复杂规律，并且利用规律对未来时刻、未知状况进行预测和判定的方法，将可应用在人类各领域内推动着大数据科技的发展。下图为目前主流的基础机器学习模型。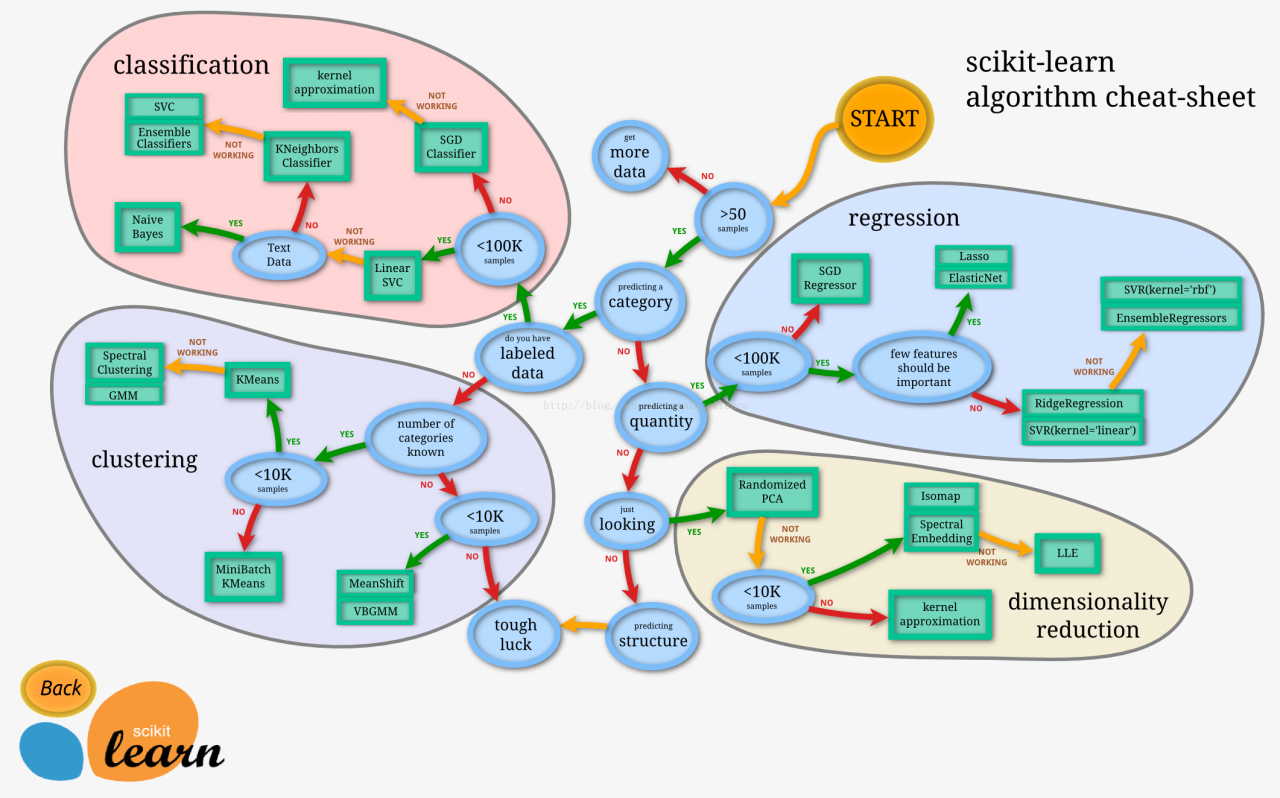

逻辑斯蒂回归

模型介绍

逻辑斯谛回归(LR)是经典的分类方法

1．逻辑斯谛回归模型是由以下条件概率分布表示的分类模型。逻辑斯谛回归模型可以用于二类或多类分类。

$$P(Y=k|x)=\frac{\exp \left(w_k\cdot x\right)}{1+{\sum }_{k=1}^{K-1}\exp \left(w_k\cdot x\right)},k=1,2,\cdots ,K-1$$

$$P(Y=K|x)=\frac{1}{1+{\sum }_{k=1}^{K-1}\exp \left(w_k\cdot x\right)}$$
这里，$x$为输入特征，$w$为特征的权值。

其中，逻辑斯蒂回归利用sigmod（对数几率函数）的激活函数将标签值压缩至0与1之间：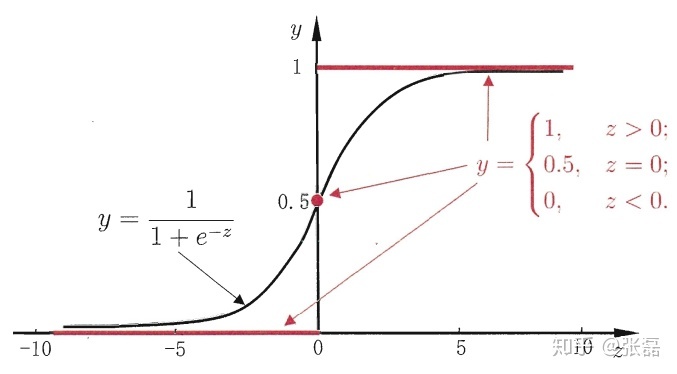

逻辑斯谛回归模型源自逻辑斯谛分布，其分布函数$F(x)$是$S$形函数。逻辑斯谛回归模型是由输入的线性函数表示的输出的对数几率模型。

2．逻辑斯谛回归模型属于对数线性模型。

3．逻辑斯谛回归模型一般采用极大似然估计，或正则化的极大似然估计。逻辑斯谛回归模型可以化为无约束最优化问题。求解该最优化问题的算法有改进的迭代尺度法、梯度下降法、拟牛顿法。

算法步骤

Logistic回归模型学习的梯度下降算法：
步骤1 取初始值$x^{(0)}\in R$，置$k=0$
步骤2 计算$f(x^{(k)})$
步骤3 计算梯度$g_k=g(x^{(k)})$，当$\Vert g_k\Vert <\epsilon$时，停止迭代，令$x^{\ast }=x^{(k)}$；否则，求${\lambda }_k$，使得$f(x^{(k)}+{\lambda }_k{g}_k)=\underset{\lambda ⩾0}{\max }f(x^{(k)}+\lambda g_k)$
步骤4 置$x^{(k+1)}=x^{(k)}+{\lambda }_k{g}_k$，计算$f(x^{(k+1)})$，当$\Vert f(x^{(k+1)})-f(x^{(k)})\Vert <\epsilon$或 $\Vert x^{(k+1)}-x^{(k)}\Vert <\epsilon$时，停止迭代，令$x^{\ast }=x^{(k+1)}$
步骤5 否则，置$k=k+1$，转(3)

模型评估

众所周知，如今有数十种机器学习算法，而各个算法中均有不同的参数可以进行使用，那么，如何判断模型的性能从而选择成本低且高效的算法模型呢？有以下几种方式：

1. 模型准确率
   准确率是指分类或预测正确的样本占总样本个数的比例，这最简单也是最直接评估模型的方法。而误差期望指的是模型预测输出结果与样本的真实输出结果的差异。此外，ROC曲线、均方误差、F1score也是评估模型准确率的计算方法。

2. 内存占用及运行速度
   不同模型使用不同参数对模型数据进行拟合的时候，均需要占用电脑的内存并发挥其GPU、CPU、TPU等软硬件的的资源与作用。选择一个适合硬件发挥、兼容性高、运行速度快的模型能够最高效率且低成本的让机器正常运行。

参考基于python的统计学习方法