NO.03
ZEYI
06.2020
正文共： 2291字
预计阅读时间： 6分钟
嘿喽，我是则已。这是stata的第三期学习。
前面学习了非参数检验，方差分析。今天来这学习：相关分析、主成分分析与因子分析。 划线部分是自己要研究的变量。 相关分析
研究各个变量之间的关系。不考虑变量之间的因果关系只研究其中的相关关系。方法有：简单相关分析，偏相关分析。 01 简单相关分析 简单相关分析是将研究变量的线性相关程度并用统计指标表示出来。
输入命令:correlate month tem hour 得到结果如下：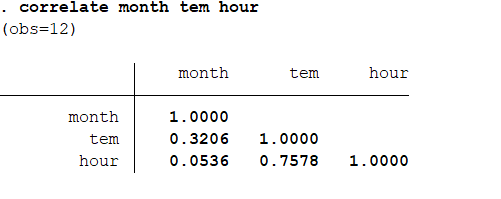
结果分析:平均日照和温度具有较高的正相关性。 还可以获取方差和协方差矩阵：correlatemonth tem hour,covariance
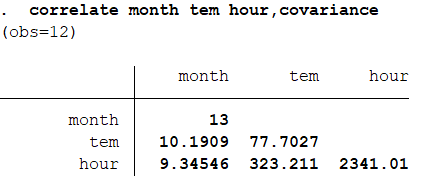最后来检验相关性的显著性：pwcorr month tem hour,sig
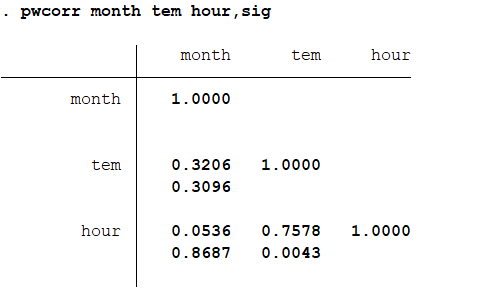结果分析：month和tem相关性检验分析的P值是为0.3096，与hour是0.8687，hour与tem的是0.043。 还有一种更精确的方法检验显著性：pwcorr month tem hour,sidak sig
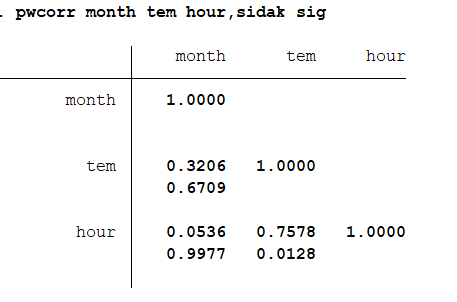结果分析：相关性的P值都有显著提高。
02 偏相关分析 因为需要进行相关性分析的变量的取值会同时受到其他变量的影响，这时候需要把其他变量控制住，然后再分析变量的系数。
输入命令: pcorr YW SX IQ 得到结果如下：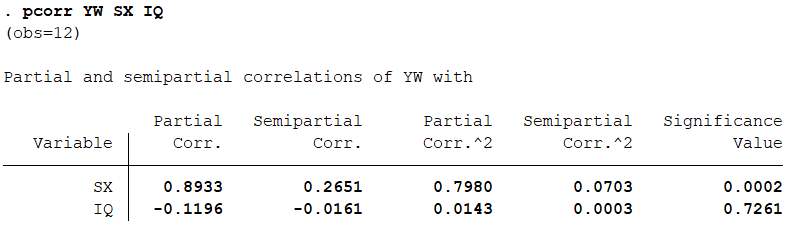
结果分析：第一列可以得到偏相关系数p.corr，最后一列可得到显著性水平value。在相关分析我们学习简单相关分析，偏相关分析。接下来是主成分分析与因子分析。 主成分分析与因子分析 变量特别多，之间还存在很强的相关关系或信息重叠，直接分析带来大量工作量，在不损失大量信息的前提下，用独立的较少变量替代原变量进行分析的方法叫主成分分析法与因子分析法。 01 主成分分析 主成分分析是在较强相关关系的情况，带来多重共线性问题。将众多初始变量整合成少数几个相互无关的主成分变量，代替以前变量进行分析
先看看几个变量之间的关系，故进行相关性分析：correlate V2-V19 得到结果如下：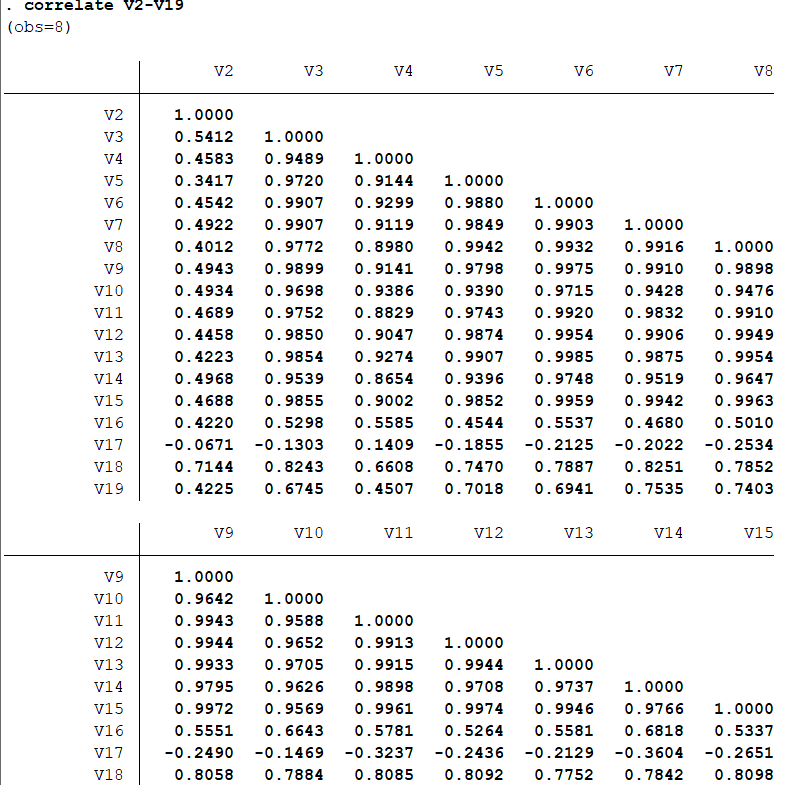
结果分析:可以发现有些变量的相关性是非常高的，适合主成分分析法 主成分分析：pca V2-V19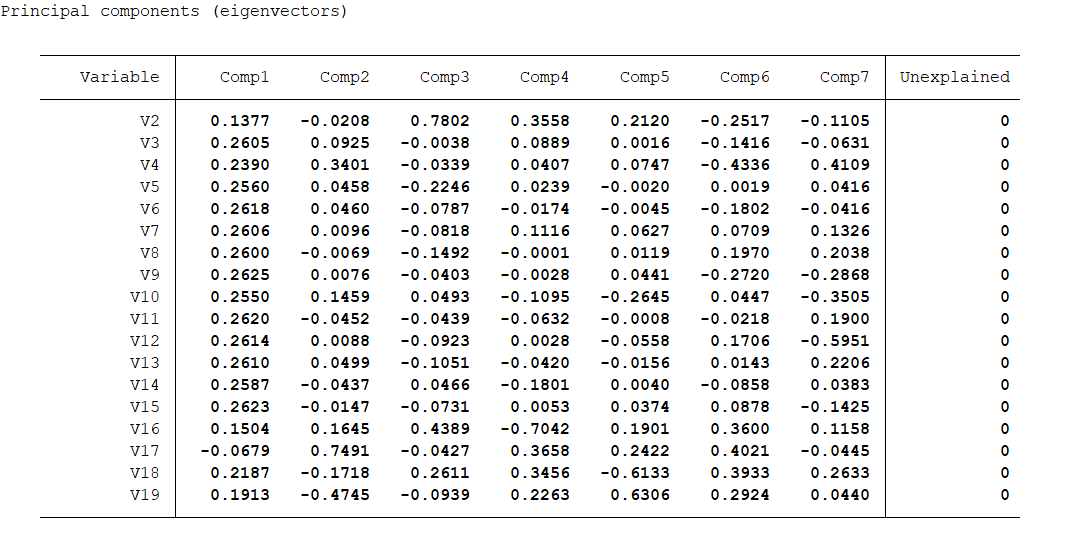
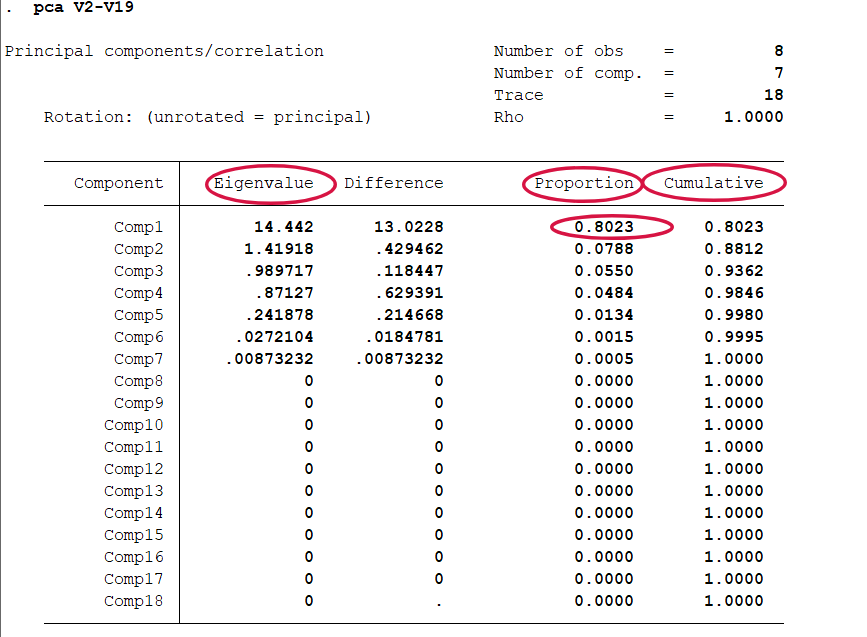结果分析：ei指特征值指主成分的解释能力，特征值越大，表明主成分成分解释能力越强。pro指贡献率，贡献率越大，例如0.8023这个主成分解释了80%的数据的信息。cumulative指累计贡献率。最后一个表示各个主成分的表达式，即它如何由原先变量组合出来的。 我们保留几个特征值大于1的主成分来建立模型：pca V2-V19,mineigen(1)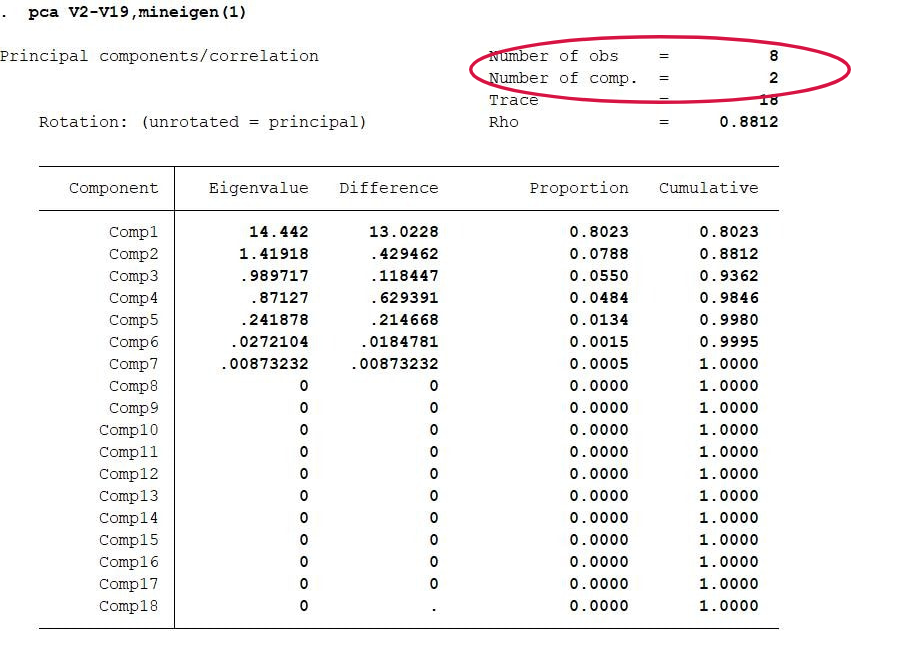
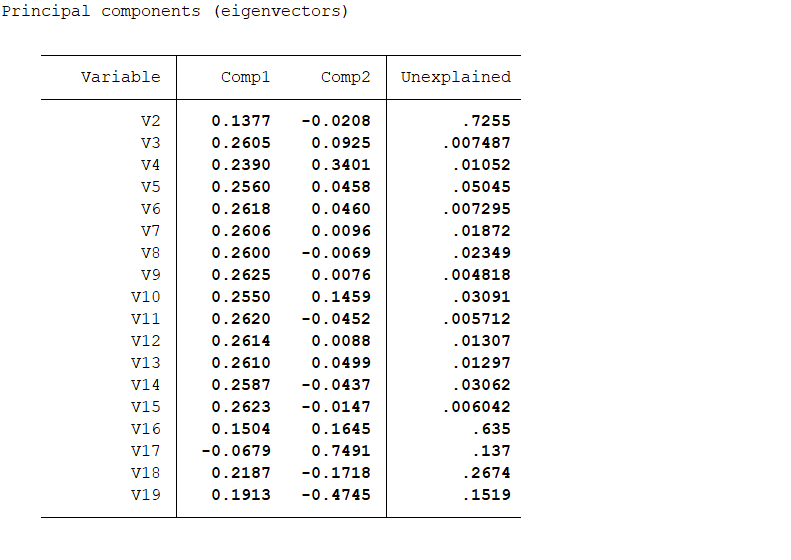结果分析：可以看出只保留了两个主成分进行分析。unexplained指该变量未被系统提取的两个主成分所解释的比例。例如V2就损失比较大，大概有72%。 当然我们也可以按照意愿限定提取主成分的个数，例如提取一个： pca V2-V19,components(1)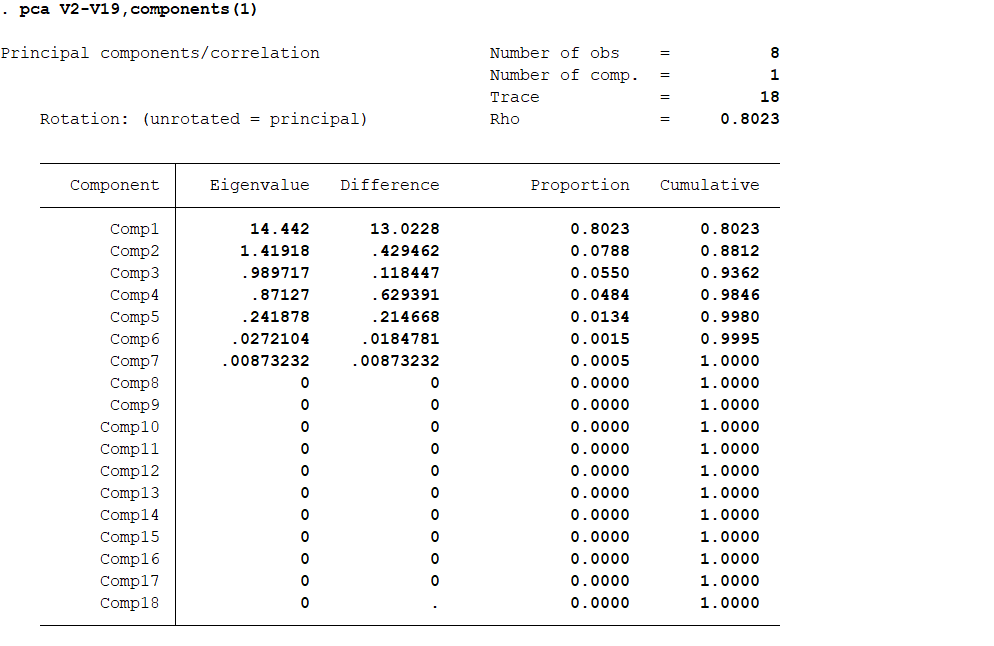
02 因子分析法 可以视为主成分分析法的深化，研究具有错综复杂关系的数据指标如何受少数几个内在的独立因子所支配，多用于处理多元分析中的降维处理。主要介绍主成分因子分析法。 主成分因子分析法
输入命令:factor V2-V7,pcf 得到结果如下：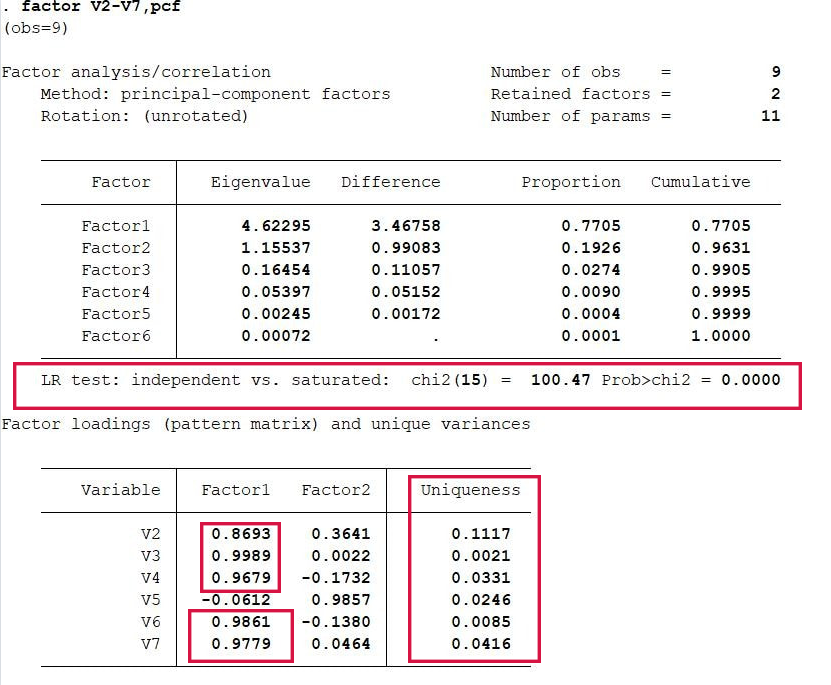
结果分析: LR卡方值是100.47。P值为0意味着模型非常显著。模型总共提取了六个因子，其中只有前两个因子的特征值是大于1的。Pro指因子的方差贡献率。提取的第一个公因子对V5解释力度小于对其他变量的解释力度。从uniqueness可以看出数据损失的信息量是比较小的。 对因子结构进行旋转：rotate
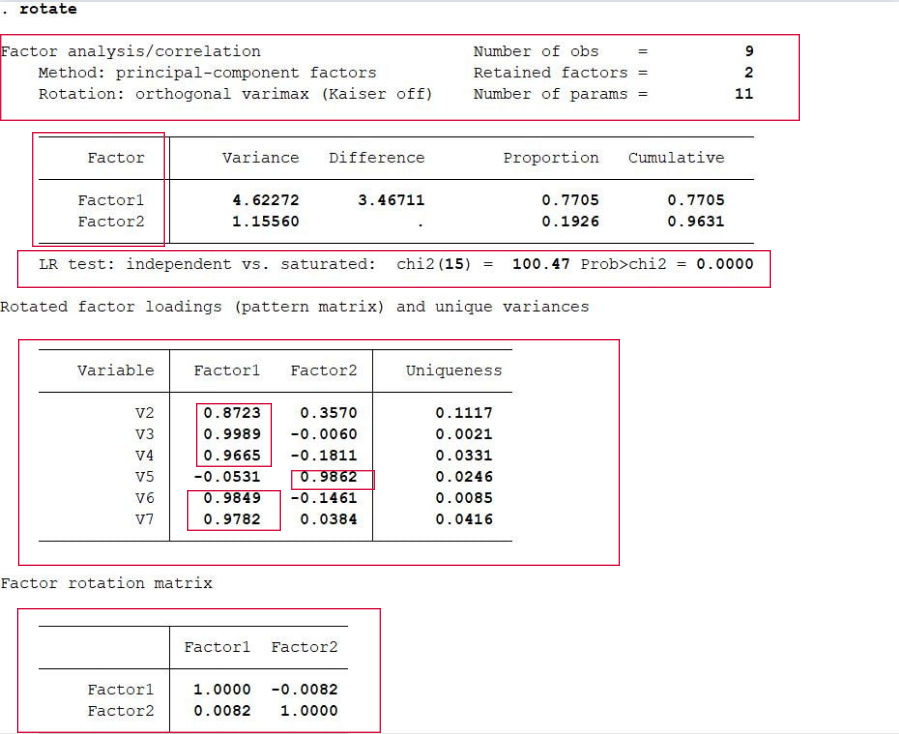结果分析： 最上部是旋转一般情况说明，第二部分表明旋转后一共提取了两个因子，卡方值和P值表明模型显著，第三部分是说明变量未被解释部分，和旋转的两个主因子对各个变量的解释程度。最后一部分因子旋转的情况，发现提取的两个公因子之间不存在相关关系。 绘制因子旋转后的因子载荷图：loadingplot,factors(2) yline(0) xline(0)
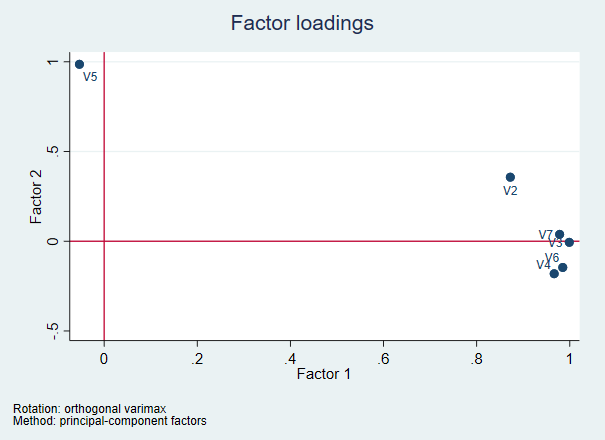图形分析：因子载荷图是用户更直观的看到各个变量被因子的解释情况，可以发现，V5主要由因子2解释，其余由因子1解释。 显示因子分析的系数矩阵：predict f1 f2
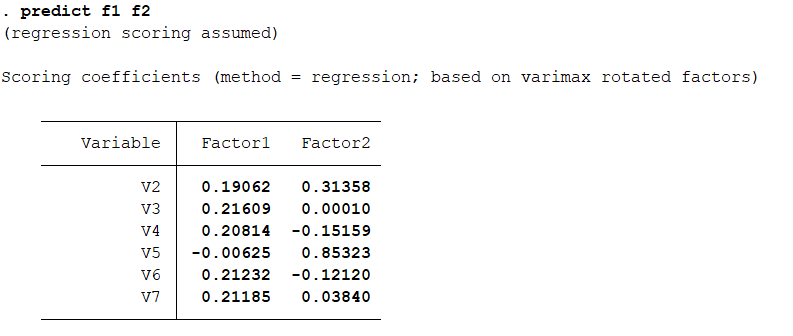结果分析： 因子分析后各个样本的得分情况，根据这个矩阵，可以写出各个因子的表达式。 查看f1、f2的值，展示每个因子的得分情况： list f1 f2
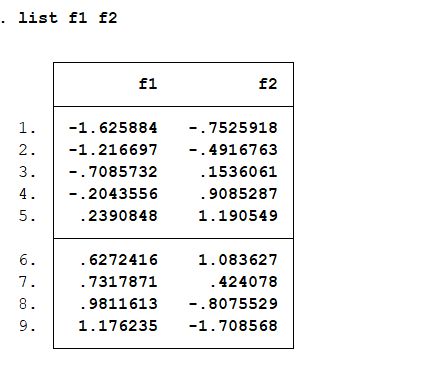观察提取的因子的相关性：correlate f1 f2
结果分析：因子之间不存在相关性说明前面旋转因子时采用系统默认方式是正确的。 展示每个样本得分因子示意图：scoreplot,mlabe(V1) yline(0) xline(0)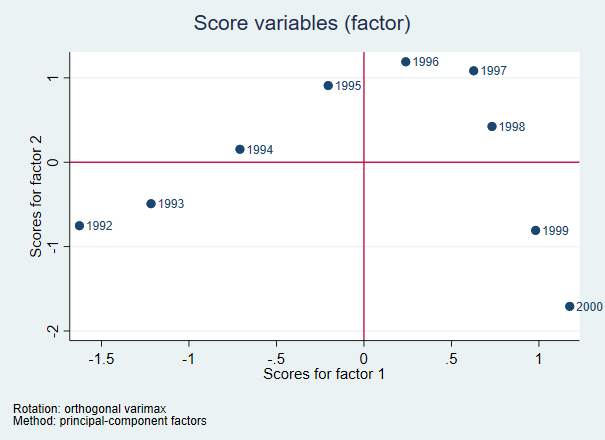
图形分析： 所有样本被分到四个象限，其中第一象限包含的是1996、1997、1998，这三年的两个因子得分都比较高，第二象限表示1994、1995因子2得分较高，因1得分较低。第三象限表示两个因子都得分较低。 进行检验：estat kmo
结果分析： 此检验是为了看数据是否适合因子分析，q取值的范围是0-1，0.9-1表示非常好，0.8-0.9表示可奖励的，0.7-0.8表示还好，0.7-0.6表示中等，0.5-0.6表示糟糕。由此看出本例因都在0.6以上，所以适合因子分析，模型构建是有意义的。 特征值的碎石图：screeplot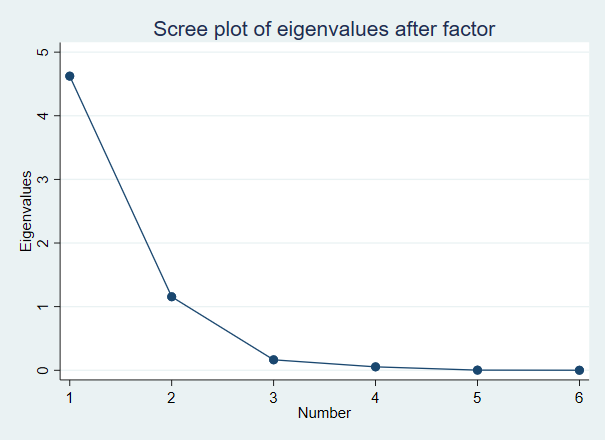
图形分析： 可以直观看到提取各个因子的特征值的大小情况，横轴表示系统提取因子的名称，纵轴为特征值大小。可以看出只有前两个特征值的因子是大于1的。好啦，今天的学习到这里！如果有什么不懂，或者需要软件和教学资源请到后台联系我。- End -
“如果喜欢这期内容 那么请关注我吧”