数据预处理的主要内容包括数据清洗、数据集成、数据变换和数据归约。
4.1 数据清洗
数据清洗主要是删除原始数据中的无关数据、重复数据,平滑噪声数据,筛选掉与挖掘主题无关的数据,处理缺失值、异常值。
4.1.1 缺失值处理
有3类:删除记录、数据插补和不处理。常用的数据插补方法如下表:

插补方法有:1、拉格朗日插值法 2、牛顿插值法
例子:用拉格朗日插值法对缺失值进行插补

4.1.2 异常值处理

4.2 数据集成
4.2.1 实体识别
实体识别是从不同数据源识别出现实世界的实体,它的任务就是统一不同源数据的矛盾之处,常见的实体识别如下:
- 同名异义
数据源A中的属性ID和数据源B中的ID分别描述的是菜品编号和订单编号,即描述的是不同的实体
2.异名同义
数据A中的sales_dt和数据源B中的salesdate都是描述销售日期的,即A.salesdt=B.sale_date
3.单位不统一
描述同一个实体时分别用的是国际单位和中国传统的计量单位。检测和解决这些冲突就是实体识别的任务。
4.2.2 冗余属性识别
数据集成往往导致数据冗余,例如:
1)同一属性多次出现;
2)同一属性命名不一致导致重复。
4.2.3 数据变换
数据变换主要是对数据进行规范化处理,将数据转换成“适当的”形式,以适用于挖掘任务及算法的需要。
4.2.4 简单函数变换
简单函数变换是对原始数据进行某些数学函数变换,常用的包括平方、开方、取对数、差分运算等。
4.2.5 规范化
数据标准化(归一化)处理是数据挖掘的一项工作。为了消除指标之间的量纲和取值范围差异的影响,需要进行标准化处理,将数据按照比例进行缩放,使之落入一个特定的区域,便于进行综合分析。如将工资收入属性值映射到[-1,1]或者[0,1]之内
1.最小-最大规范化
x*=x-min/max-min
2.零-均值规范化
零-均值规范化也叫标准差标准化,经过处理的数据的均值为0,标注差为1.
3.小数定标规范化
通过移动属性值的小数位数,将属性值映射到[-1,1]之间,移动的小数位数取决于属性值绝对值的最大值
数据规范化例子:

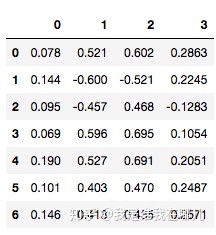
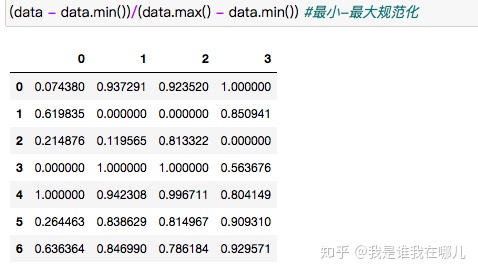
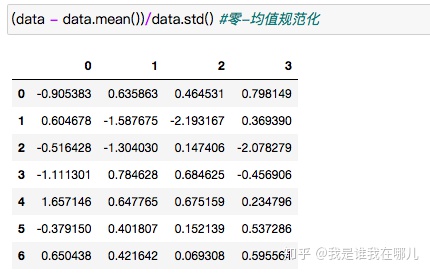
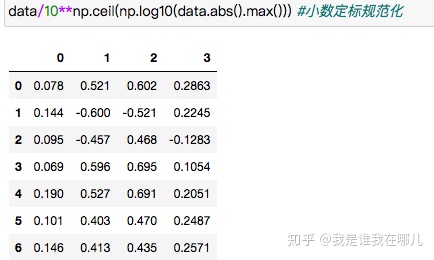
4.2.6 连续属性离散化
1.离散化的过程
连续属性离散化就是在数据的取值范围内设置若干个离散的划分点,将取值范围分为一些离散化的区间,最后用不同的符号或整数值代表落在每个子区间中的数据值。所以,离散化设计两个字任务:确认分类数以及如何将连续属性值映射到这些分类值。
2.常用的离散化方法
1)等宽法
类似于制作频数分布图,将属性分布值分为几个等分的分布区间;
2)等频法
将相同数量的记录放入每个区间;
3)基于聚类的分析方法
将属性按照K-means算法进行聚类,然后根据聚类的分类,将同一聚类的记录合并到同一组内。
例子:对医学中中医证型的相关数据进行离散化

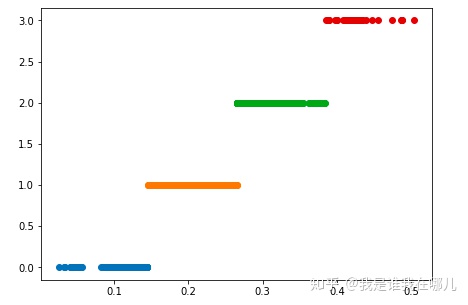
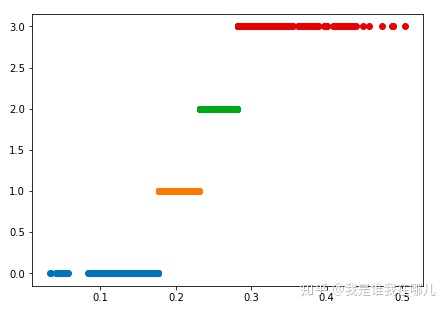
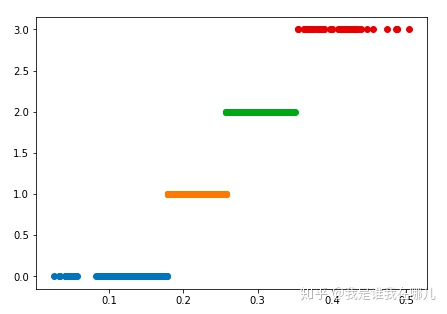
分别用等宽法、等频法和(一维)聚类对数据进行离散化,将数据分成4类,然后将每一类记为同一个标识,如分别记为A1,A2,A3,A4,再进行建模。
4.2.7 属性构造
在数据挖掘过程中,为了帮助用户提取更有用的信息,挖掘更深层次的模式,提高挖掘结果的精度,需要利用已有的属性集构造出新的属性,并加入到现有的属性集合中。
4.2.8 小波变换
信号分析手段,具有多分辨率的特点,在时域和频域都具有表征信号局部特征的能力,通过伸缩和平移等运算过程对信号进行多尺度的聚焦分析,提供了一种非平稳信号的时频分析手段,可以由粗及细地逐步观察信号,从中提取有用信息。能够刻画某个问题的特征量往往是隐含在一个信号中的某个或者某些分量。小波变换可以把非平稳信号分解为表达不同层次、不同频带信息的数据序列,即小波系数。(这边有点难,先码着p90)
4.3 数据归约
在大数据集上进行复杂的数据分析和挖掘需要很长时间。数据归约产生更小且保持原数据完整性的新数据集,在归约后的数据集上进行分析和挖掘将提高效率。数据归约的意义在于:
1)降低无效、错误数据对建模的影响,提高建模的准确性。
2)少量且具有代表性的数据将大幅缩减数据挖掘所需的时间。
3)降低储存数据的成本。
4.3.1 属性归约
属性归约通过属性合并创建新属性维数,或者通过直接删除不想关的属性(维)来减少数据维数,从而提高数据挖掘的效率,降低计算成本。属性归约的目标是寻找最小的属性子集并确保新数据子集的概率分布可能接近原来数据集的概率分布。属性归约常用方法见表:
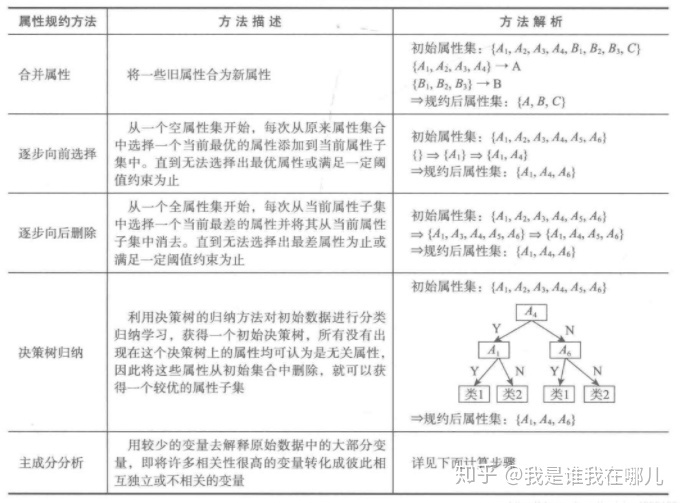
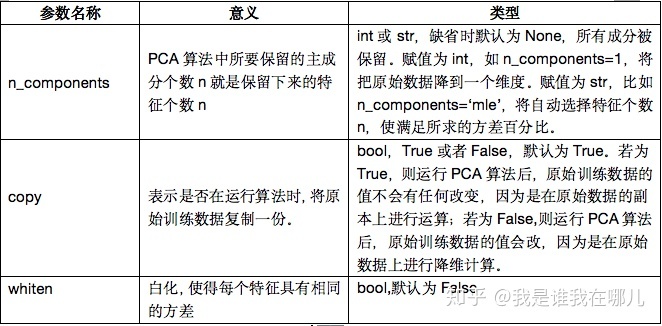
主成分分析:pyhon中,主成分分析的函数位于scikit-learn库下,其使用格式如下,参数说明如下表。
sklearn.decomposition.PCA(n_components=None,copy=True,whiten=False)
例子:

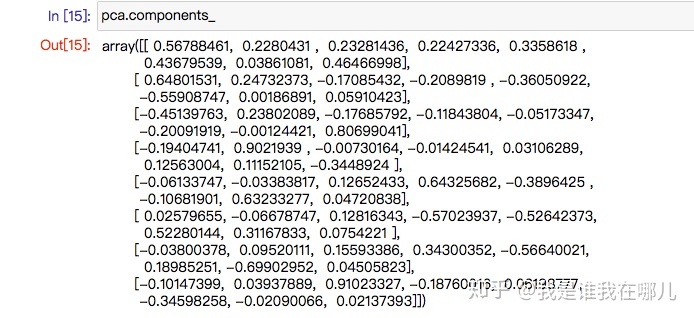
从上面的结果可以得到特征方程有8个特征根、对应的8个单位特征向量以及各个成分各自的方差百分比。


4.3.2 数值归约
数值归约通过选择替代的、较小的数据来减少数据量,包括有参数方法和无参数方法两类。
1)有参数方法:使用一个模型来评估数据,只需要存放参数,而不需要存放实际数据,例如回归(线性回归和多元回归)和对数线性模型。
2)无参数方法:需要存放实际数据,例如直方图、聚类、抽样(采样)
1.直方图 2.聚类3.抽样 4.参数回归
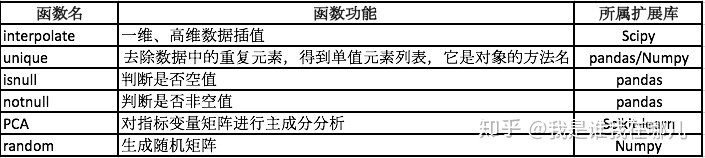
4.4 python主要数据预处理函数
主要是python中的插值、数据归一化、主成分分析等与数据预处理相关的函数
具体请见:《python数据分析与挖掘实战》第4章