目录
4. t-SNE（t-Distributed Stochastic Neighbor Embedding）
（1）在高维空间构建一个概率分布拟合高维样本点间的相对位置关系。
（2）在低维空间，也构建一个概率分布，拟合低维样本点之间的位置关系。
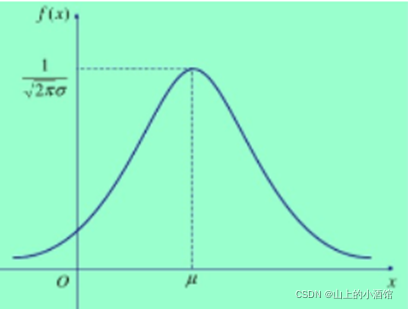
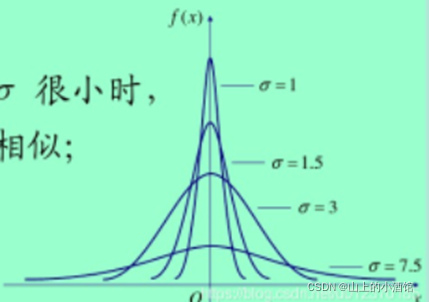
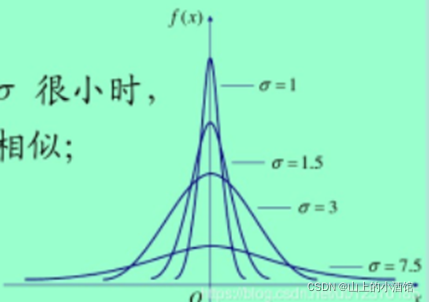
1.高斯分布：
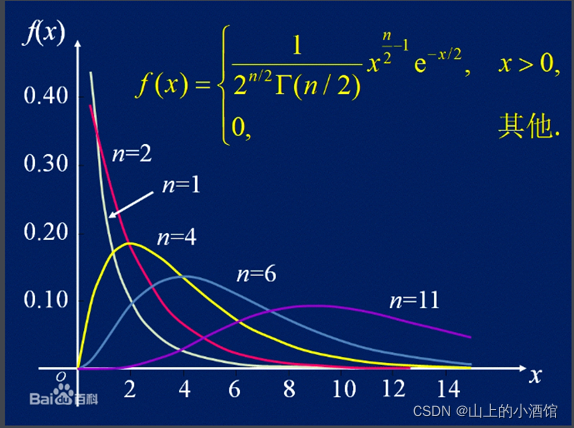
2.卡方分布：
若n个相互独立的随机变量， 均服从标准正态分布（独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律成为x2分布，参数n=v，记为Q~x2（v）。
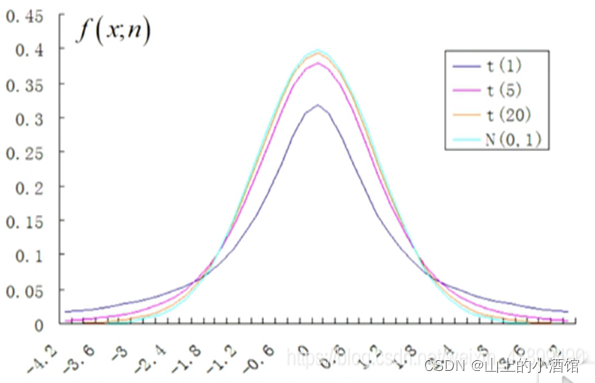
3.t分布
设随机变量X~ N(0,1)（标准正态分布）,Y~x2 (n)（自由度为n的卡方分布），且X与Y相互独立，则称随机变量 服从自由度为n的t分布，t分布在自由度较低时相对标准正态分布表现更柔和（矮胖）。记为：
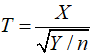
4. t-SNE（t-Distributed Stochastic Neighbor Embedding）
（1）在高维空间构建一个概率分布拟合高维样本点间的相对位置关系。
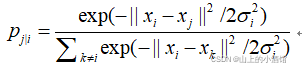
以样本xi为中心，不同样本点与xi的相对位置的概率分布。
衡量两个样本间的距离，距离越大，概率
越小。分母累加求和为了归一化。
（2）在低维空间，也构建一个概率分布，拟合低维样本点之间的位置关系。
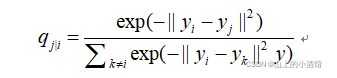
（3） 通过学习，调整低维数据点，令两个分布接近。利用KL散度（距离）衡量两个分布之间的差异。通过梯度下降调整低维空间的样本点y使得C变小，实现降维。
目标：yi对应xi投影到低维空间，调整yj使得KL散度（可看做损失函数）最小，即低维空间与高位空间的位置分布尽可能一致。
本质：高维空间样本位置关系的分布投影至低维空间时保持不变。
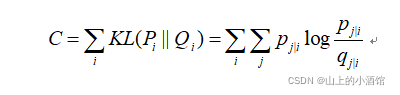
5. SNE的缺点以及解决措施
（1）距离不对称，
利用联合概率代替条概率。
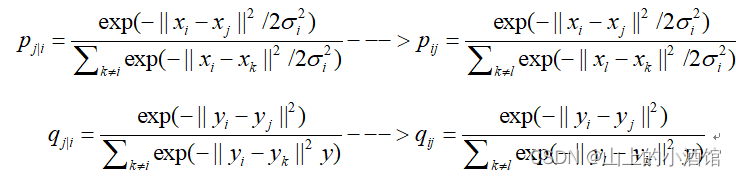
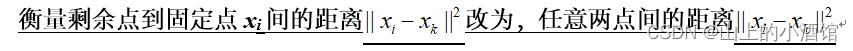
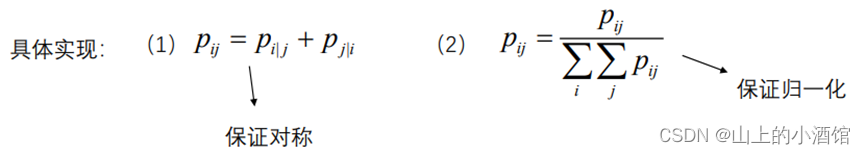
（2）拥挤现象
从高维到低维进行转换的过程中，低维点的距离无法建模高维点之间的位置关系。高维空间中距离较大的点对，在低维空间距离会变得较小。
解决：利用拖尾较大的t分布对低维点建模。
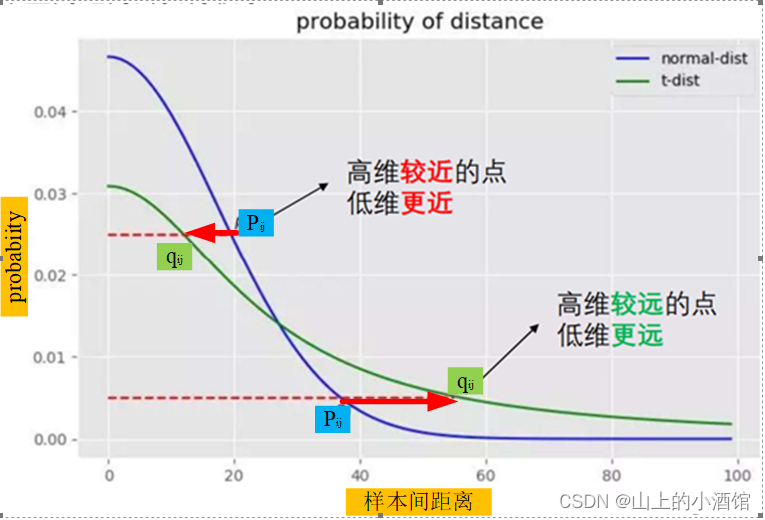
使用t分布后，在正态分布中距离较小的点，可保持相同的概率在t分布中获得更小的距离（拉近高维空间中距离较近的点）。在正态分布中距离较大的点，可保持相同的概率在t分布中获得更大的距离（排斥高维空间中距离较远的点）。
（3）
的物理意义，影响高维空间中高斯分布的形状，
类似于K紧邻中的搜索半径，当xi临近点较多时，减小 ；当xi临近点较少时，增大 。
t-SNE是一种集降维与可视化于一体的技术，它是基于SNE可视化的改进，解决了SNE在可视化后样本分布拥挤、边界不明显的特点，是目前最好的降维可视化手段。
t-SNE目标函数：原空间与嵌入空间样本分布之间的KL散度。
t-SNE优化算法：梯度下降。
t-SNE注意问题：KL散度作目标函数是非凸的，对初值敏感，需要多次初始化以防止陷入局部次优解
（4）影响效果的参数
perplexity混乱度。混乱度越高，t-SNE将考虑越多的邻近点，更关注全局。因此，对于大数据应该使用较高混乱度，较高混乱度也可避免噪声的影响。相对而言，该参数对可视化效果影响不大。
early exaggeration factor 该值表示期望的簇间距大小，如果太大的话（大于实际簇的间距），将导致目标函数无法收敛。相对而言，该参数对可视化效果影响较小，默认就行。
learning rate学习率。关键参数，根据具体问题调节。
maximum number of iterations迭代次数。迭代次数不能太低，建议1000以上。
angle (not used in exact method)角度。相对而言，该参数对效果影响不大。
T-SNE就是一种数据降维的算法，其成立的前提是基于这样的假设：尽管现实世界中的许多数据集是嵌入在高维空间中，但是都具有很低的内在维度。即高维数据经过降维后，在低维状态下更能显示出其本质特性。这就是流行学习的基本思想，也称为非线性降维。
参考：
(1条消息) t-SNE高维数据可视化（python）_haoji007的博客-CSDN博客_python高维数据可视化
https://blog.csdn.net/haoji007/article/details/94962952python与人工智能-数据降维-t-SNE_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1cU4y1w74A?spm_id_from=333.337.top_right_bar_window_history.content.click